Лаба_1 — копия

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное автономное образовательное учреждение высшего образования

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»

ИНСТИТУТ ВЫЧИСЛЕТИЛЬНЫХ СИСТЕМ И ПРОГРАММИРПОВАНИЯ

КАФЕДРА № 41

ОЦЕНКА

ПРЕПОДАВАТЕЛЬ

ассистент				Е. К. Григорьев
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ № 1

ИССЛЕДОВАНИЕ ДАТЧИКОВ РАВНОМЕРНО РАСПРЕДЕЛЕННЫХ ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ

по дисциплине: Моделирование

РАБОТУ ВЫПОЛНИЛА

СТУДЕНТКА ГР. №
	номер группы		подпись, дата		инициалы, фамилия

Санкт-Петербург 2021

Цель работы: Целью работы является ознакомление с методами и алгоритмами получения в программной среде MATLAB псевдослучайных чисел, равномерно распределенных на интервале (0,1), а также изучение тестов для проверки качества генерируемых чисел.

Мультипликативный датчик

1. N=100

Листинг программы:

clear all

m=10;

N=100;

R=[];

M=65093;

R(1)=2^-m;

for i=2:1:N+1

R(i)=M*R(i-1);

R(i)=R(i)-fix(R(i));

end

figure(1)

hist(R)

grid on

xlabel("Значение");

ylabel("Частота");

axis([0 1 0 20]);

M_e=mean(R);

D_e=var(R);

На рисунке 1 изображена гистограмма, математическое ожидание и дисперсия для мультипликативного датчика при N=100.

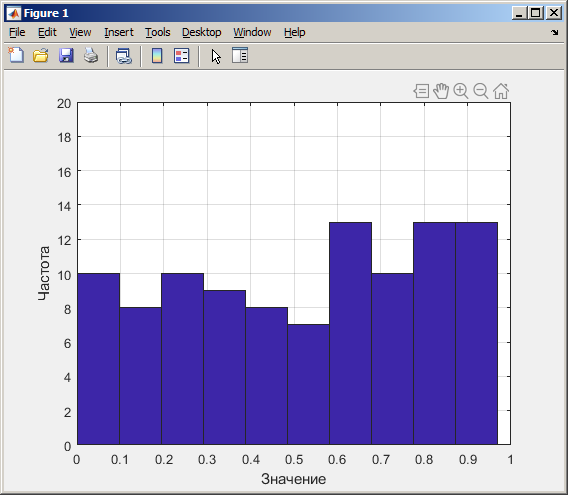
Рисунок 1 – Гистограмма, математическое ожидание и дисперсия для мультипликативного датчика при N=100

2. N=500

Листинг программы:

clear all

m=10;

N=500;

R=[];

M=65093;

R(1)=2^-m;

for i=2:1:N+1

R(i)=M*R(i-1);

R(i)=R(i)-fix(R(i));

end

figure(1)

hist(R)

grid on

xlabel("Значение");

ylabel("Частота");

axis([0 1 0 70]);

M_e=mean(R);

D_e=var(R);

На рисунке 2 изображена гистограмма, математическое ожидание и дисперсия для мультипликативного датчика при N=500.

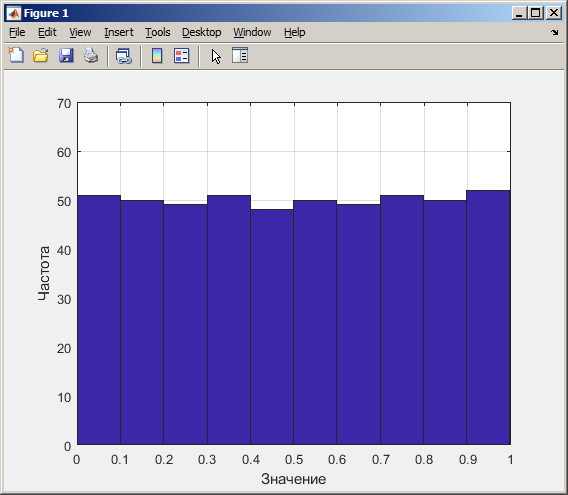
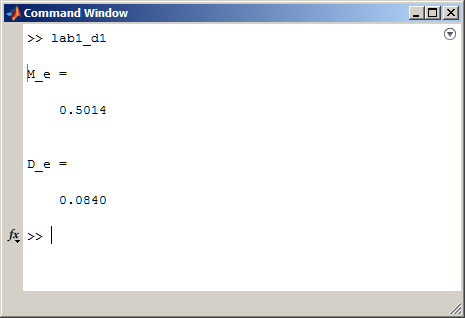
Рисунок 2 - Гистограмма, математическое ожидание и дисперсия для мультипликативного датчика при N=500

3. N=1000

Листинг программы:

clear all

m=10;

N=1000;

R=[];

M=65093;

R(1)=2^-m;

for i=2:1:N+1

R(i)=M*R(i-1);

R(i)=R(i)-fix(R(i));

end

figure(1)

hist(R)

grid on

xlabel("Значение");

ylabel("Частота");

axis([0 1 0 120]);

M_e=mean(R);

D_e=var(R);

На рисунке 3 изображена гистограмма, математическое ожидание и дисперсия для мультипликативного датчика при N=1000.

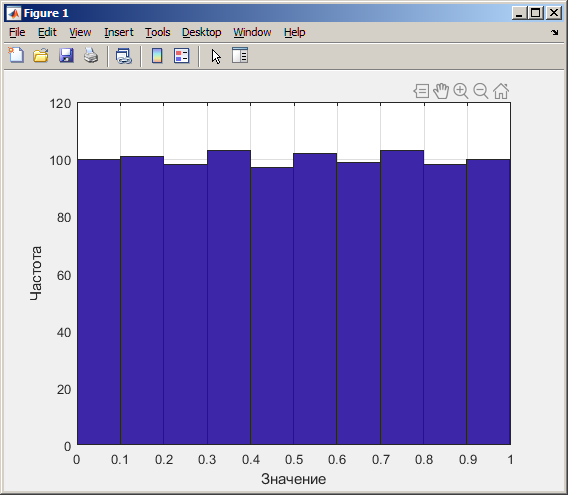
Рисунок 3 - Гистограмма, математическое ожидание и дисперсия для мультипликативного датчика при N=1000

Линейный конгруэнтный датчик

1. N=100

Листинг программы:

clear all

N=100;

R=[];

R(1)=0;

for i=2:1:N+1

R(i)=11*R(i-1)+pi;

R(i)=R(i)-fix(R(i));

end

figure(1)

hist(R)

grid on

xlabel("Значение");

ylabel("Частота");

axis([0 1 0 20]);

M_e=mean(R);

D_e=var(R);

На рисунке 4 изображена гистограмма, математическое ожидание и дисперсия для линейного конгруэнтного датчика при N=100.

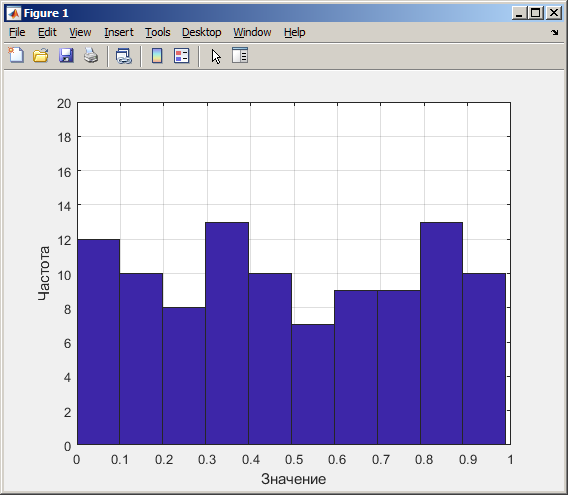
Рисунок 4 – Гистограмма, математическое ожидание и дисперсия для линейного конгруэнтного датчика при N=100

2. N=500

Листинг программы:

clear all

N=500;

R=[];

R(1)=0;

for i=2:1:N+1

R(i)=11*R(i-1)+pi;

R(i)=R(i)-fix(R(i));

end

figure(1)

hist(R)

grid on

xlabel("Значение");

ylabel("Частота");

axis([0 1 0 70]);

M_e=mean(R);

D_e=var(R);

На рисунке 5 изображена гистограмма, математическое ожидание и дисперсия для линейного конгруэнтного датчика при N=500.

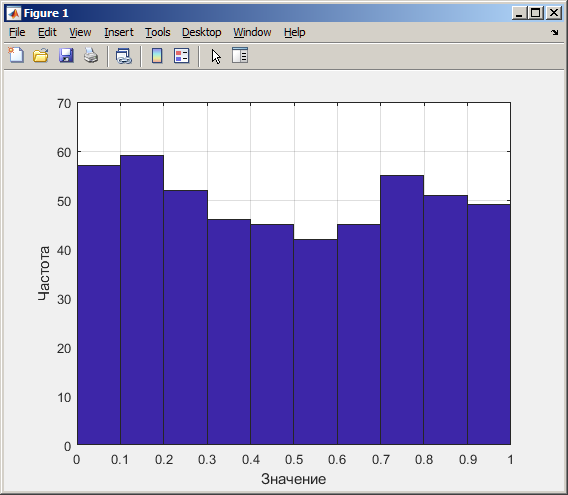
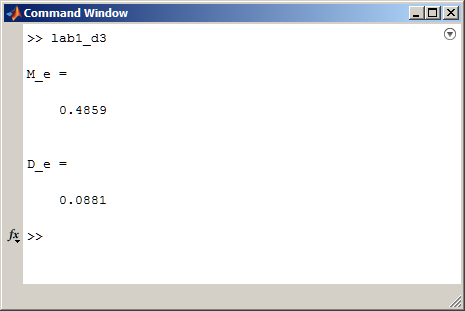
Рисунок 5 – Гистограмма, математическое ожидание и дисперсия для линейного конгруэнтного датчика при N=500

3. N=1000

Листинг программы:

clear all

N=1000;

R=[];

R(1)=0;

for i=2:1:N+1

R(i)=11*R(i-1)+pi;

R(i)=R(i)-fix(R(i));

end

figure(1)

hist(R)

grid on

xlabel("Значение");

ylabel("Частота");

axis([0 1 0 20]);

M_e=mean(R);

D_e=var(R);

На рисунке 6 изображена гистограмма, математическое ожидание и дисперсия для линейного конгруэнтного датчика при N=1000.

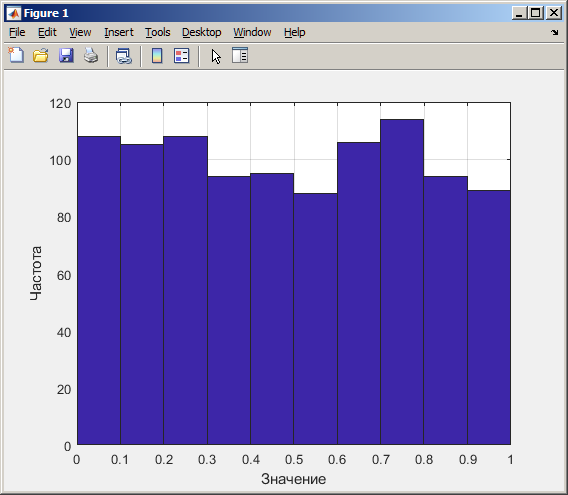
Рисунок 6 – Гистограмма, математическое ожидание и дисперсия для линейного конгруэнтного датчика при N=1000

Теоретическое вычисление математического ожидания и дисперсии

1. Математическое ожидание:

2. Дисперсия:

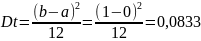
Вывод: в ходе лабораторной работы были изучены методы и алгоритмы получения в программной среде MATLAB псевдослучайных чисел, равномерно распределенных на интервале (0,1), а также изучение тестов для проверки качества генерируемых чисел.