Лекция 4 Криптосистемы Рабина,Уильямса, Голдвассера-Микали, Эль-Гамаля и ДиффиХеллмана
Криптосистема Рабина
;
1979г.
Генерирование ключей
Эта процедура выполняется при помощи следующих шагов: 1) необходимо генерировать два простых числа р и q примерно одинаковой разрядности p = q = 3 (mod 4 ) ;
2)вычислить n = p q
3)выбрать в качестве открытого ключа - п, а в качестве закрытого – его множители р,q.
,
Шифрование
Если пользователь В хочет зашифровать сообщение М для пользователя А, то он выполняет следующие шаги:
1)получает открытый ключ n пользователя А;
2)представляет сообщение М в виде последовательности блоков
такой длины, что сообщение из каждого блока может быть задано целым числом Mi (0,1, 2, ..., n −1);
3) |
вычисляет криптограмму |
Ci = Mi |
, |
i =1, 2, ... |
|
|
mod n |
||
|
|
2 |
|
|
4) |
Отправляет rкриптограмму C=C1,C2…Ck , пользователю А. |
|||
Дешифрование криптограммы
1) Зная р и q, пользователь А реализует полиномиально сложный
алгоритм для нахождения 2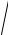
Сi (подразд. 2.2.1), т. е. пользователь А
находит четыре корня: M1, M2 , M3, M4 ;
2) используя избыточность, содержащуюся в сообщении, пользователь А определяет какое из этих четырех сообщений является истинным. Если в сообщении отсутствует естественная избыточность, то ее необходимо ввести до шифрования (например, повторив несколько последних бит сообщения).
Метод решения квадратного уравнения по составному модулю
1) |
вычисляют |
|
mod p , т. е. находят два корня +r , −r по mod p; |
|
a |
||||
2) |
аналогично вычисляют корни −s , +s по mod q; |
|||
3) |
используя рассмотренный в разд. 2 алгоритм, находят числа c и d, |
|||
такие, что c p +d q =1 ; |
(r d q + s c p)mod n , y = (r d q −s c p)mod n; |
|||
4) |
рассчитывают x = |
|||
5) |
в качестве решения |
a mod n выбирают числа ± x(mod n), ± y(mod n). |
||
Видно, что схема Рабина обеспечивает простое генерирование ключей, а также весьма простой алгоритм шифрования, но имеет сложный алгоритм дешифрования. Данный метод можно рекомендовать в тех случаях, где шифрование должно быть простым, а при дешифровании этого не требуется.
Истинное сообщение из 4-х возможных находится на основе анализа избыточности сообщения. При отсутствии избыточности она должна быть внесена в сообщение до его шифрования, например, путем повторения некоторых символов.
Дополнительные комментарии по алгоритму дешифрования
Дешифрование равносильно нахождению корня уравнения
r =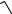 
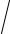a mod p
Простое число p может быть представлено
либо как p=4k+3, либо как p=4k+1, где k положительное целое число.
В первом случае вычет находится просто:
-найти r=a^(p+1)/4modp, -выдать в качестве ответа (r,-r).
Имея в своем распоряжении метод генерирования невычетов b, можно использовать следующую конструкцию для нахождения 
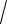a mod p
[2, 3]: |
|
|
|
|
|
|
|
|
|
1) генерировать случайные числа b Z p |
, Z p ={0,1, 2, 3, , p −1} , |
||||||
|
до тех пор, пока b2 – 4a не окажется квадратичным невычетом по mod |
|||||||
|
p, т. е. |
|
2 |
−4a |
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
p |
= −1 |
|
|
|
|
|
|
|
|
|
|
||
|
2) найти |
r = x(p+1)2 |
mod(x2 −bx + a), |
|
|
|
||
|
где |
(x2 −bx + a) |
|
- полином над полем GF(p) |
||||
3) выдать ответ: r, -r – как решение задачи |
|
|
mod p . |
|||||
|
a |
|||||||
Можно использовать алгоритм Чипполы (см. следующий слайд).