
ОТС 2 курс 2 семестр / ОТС 7.1
.docxМинистерство цифрового развития, связи и массовых коммуникаций
Федеральное государственное бюджетное образовательное учреждение высшего образования
«Поволжский государственный университет телекоммуникаций и информатики»
Факультет Базового телекоммуникационного образования
Направление
(специальность) Инфокоммуникационные технологии и системы связи
Предмет Общая теория связи
Лабораторная работа
Кодирование дискретных источников
Выполнил студенты группы ИКТп – 91 Ядринцев С.М.
Махов Н. С.
Самара 2021г.
Цель работы: целью работы является изучение методов кодирования дискретных источников на примере сжатия текстов на русском языке.
Исследование энтропийных методов кодирования
По Шеннону-Фано
Коэффициент сжатия: r = 88,3 %.
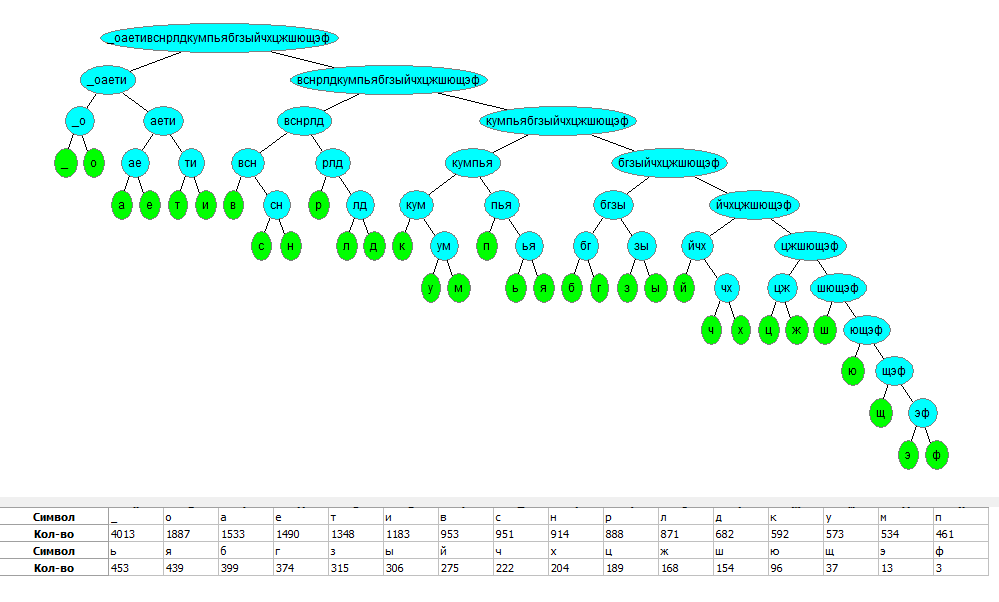
Дерево
Словарь:
Кол-во Символ Код Длина Вес
4013 _ 000 3 0,5346
1887 о 001 3 0,2514
1533 а 0100 4 0,2723
1490 е 0101 4 0,2647
1348 т 0110 4 0,2394
1183 и 0111 4 0,2101
953 в 1000 4 0,1693
951 с 10010 5 0,2111
914 н 10011 5 0,2029
888 р 1010 4 0,1577
871 л 10110 5 0,1934
682 д 10111 5 0,1514
592 к 11000 5 0,1314
573 у 110010 6 0,1527
534 м 110011 6 0,1423
461 п 11010 5 0,1024
453 ь 110110 6 0,1207
439 я 110111 6 0,1170
399 б 111000 6 0,1063
374 г 111001 6 0,0996
315 з 111010 6 0,0839
306 ы 111011 6 0,0815
275 й 111100 6 0,0733
222 ч 1111010 7 0,0690
204 х 1111011 7 0,0634
189 ц 1111100 7 0,0587
168 ж 1111101 7 0,0522
154 ш 1111110 7 0,0479
96 ю 11111110 8 0,0341
37 щ 111111110 9 0,0148
13 э 1111111110 10 0,0058
3 ф 1111111111 10 0,0013
n`=4,42
Модифицированный текст
Статистика модифицированного текста:
Длина текста: L = 22520 [символов].
Объём алфавита: K = 32 [символов].
Энтропия: H(A) = 4,36 [бит/символ].
H(A) ~= n`
Сжатый текст
Статистика сжатого (двоичного) текста:
Длина текста: L = 99463 [бит].
Объём алфавита: K = 2 [символов].
Энтропия: H(A) = 1,00 [бит/символ].
Энтропия сжатого текста равна 1, так как в алфавите всего 2 символа
Восстановленный текст имеет ошибки, это связано с тем, что мы добавили шум.
Длина восстановленного текста: 22547 [символов].
Длина несжатого текста: 22520 [символов].
Код Хаффмана
Коэффициент сжатия: r = 88,0 %.
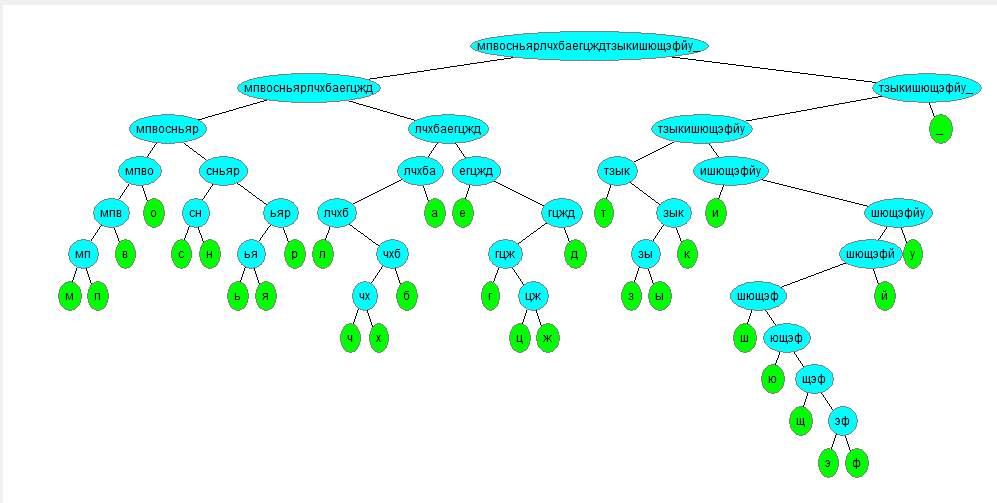
Дерево
Словарь
Кол-во Символ Код Длина Вес
4013 _ 11 2 0,3564
1887 о 0001 4 0,3352
1533 а 0101 4 0,2723
1490 е 0110 4 0,2647
1348 т 1000 4 0,2394
1183 и 1010 4 0,2101
953 в 00001 5 0,2116
951 с 00100 5 0,2111
914 н 00101 5 0,2029
888 р 00111 5 0,1972
871 л 01000 5 0,1934
682 д 01111 5 0,1514
592 к 10011 5 0,1314
573 у 10111 5 0,1272
534 м 000000 6 0,1423
461 п 000001 6 0,1228
453 ь 001100 6 0,1207
439 я 001101 6 0,1170
399 б 010011 6 0,1063
374 г 011100 6 0,0996
315 з 100100 6 0,0839
306 ы 100101 6 0,0815
275 й 101101 6 0,0733
222 ч 0100100 7 0,0690
204 х 0100101 7 0,0634
189 ц 0111010 7 0,0587
168 ж 0111011 7 0,0522
154 ш 1011000 7 0,0479
96 ю 10110010 8 0,0341
37 щ 101100110 9 0,0148
13 э 1011001110 10 0,0058
3 ф 1011001111 10 0,0013
n` = 4,40
Модифицированный текст
Статистика модифицированного текста:
Длина текста: L = 22520 [символов].
Объём алфавита: K = 32 [символов].
Энтропия: H(A) = 4,36 [бит/символ].
Н(А) ~= n`
Сжатый текст
Статистика сжатого (двоичного) текста:
Длина текста: L = 99066 [бит].
Объём алфавита: K = 2 [символов].
Энтропия: H(A) = 0,99 [бит/символ].
Восстановленный текст имеет ошибки, это связано с тем, что мы добавили шум.
Длина восстановленного текста: 22555 [символов].
Длина несжатого текста: 22520 [символов].
Вывод: код Шеннона-Фано имеет меньше ошибок, чем код Хаффмана, но оба кода не устойчивы к шуму.
Исследование словарных методов кодирования
LZ78
Оптимальный размер словаря: 4096
Длина кодового слова: n = 17 [бит].
Коэффициент сжатия: r = 86,1 %.
Длина восстановленного текста: 22520 [символов].
Длина несжатого текста: 22520 [символов].
Текст был восстановлен без потерь
Словарь:
Максимальный размер словаря: 4096 [записей].
Реальный размер словаря: 4096 [записей].
Длина наибольшего фрагмента: 12 [символов].
Длина кодового слова: n = 17 [бит].
При добавлении шума, появляются ошибки:
Восстановление сжатого текста с использованием алгоритма Лемпела-Зива (LZ78).
Длина восстановленного текста: 22895 [символов].
Длина несжатого текста: 22520 [символов].
LZW
Оптимальный размер словаря: 4096
Длина кодового слова: n = 12 [бит].
Коэффициент сжатия: r = 80,6 %.
Восстановление сжатого текста с использованием алгоритма Лемпела-Зива-Уэлша (LZW).
Длина восстановленного текста: 22520 [символов].
Длина несжатого текста: 22520 [символов].
Текст был восстановлен без потерь.
Словарь:
Максимальный размер словаря: 4096 [записей].
Реальный размер словаря: 4096 [записей].
Длина наибольшего фрагмента: 11 [символов].
Длина кодового слова: n = 12 [бит].
При добавлении шума, появляются ошибки:
Восстановление сжатого текста с использованием алгоритма Лемпела-Зива-Уэлша (LZW).
Длина восстановленного текста: 23073 [символов].
Длина несжатого текста: 22520 [символов].
LZ77
Оптимальный размер словаря: 8192
Длина кодового слова: n = 22 [бит].
Длина наибольшего фрагмента: 31 [символов].
Коэффициент сжатия: r = 71,2 %.
Восстановление сжатого текста с использованием алгоритма Лемпела-Зива (LZ77).
Длина восстановленного текста: 22520 [символов].
Длина несжатого текста: 22520 [символов].
Текст был восстановлен без потерь.
Словарь: отсутствует
При добавлении шума, появляются ошибки:
Восстановление сжатого текста с использованием алгоритма Лемпела-Зива (LZ77).
Длина восстановленного текста: 23229 [символов].
Длина несжатого текста: 22520 [символов].
Вывод: наиболее эффективным способом сжатия является LZ77, однако он в нём наблюдается наибольшее расхождение между исходным и восстановленным текстами. Наименьшее расхождение было получено при использовании кодов Шеннона-Фано и Хаффмана.
