Послание из прошлого: эти задачи нам препод дал на итоговом занятии (зачёт), имейте их ввиду тоже 1.Определить дисперсию Dn () пуассоновского потока заявок при коэффициенте загрузки, равном 1=0,9 .

Вероятность р мала, а число n велико (np = 90 < 10). Значит случайная величина Х – распределена по Пуассоновскому распределению. Составим закон распределения. Случайная величина X имеет область значений (0,1,2,...,m). Вероятности этих значений можно найти по формуле: Найдем ряд распределения X. Здесь λ = np = 100*0.9 = 90 P(0) = e^{- λ} = e^-90 = 0 Математическое ожидание. M[X] = λ = 90 Дисперсия. D[X] = λ = 90

2. Определить второй начальный момент m^2 (p) для пуассоновского потока заявок, при коэффициенте загрузки, равном 1=0,9 .

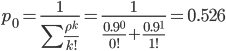1. Интенсивность нагрузки. Интенсивность нагрузки ρ=0.9 показывает степень согласованности входного и выходного потоков заявок канала обслуживания и определяет устойчивость системы массового обслуживания. 2. Время обслуживания (мин). 3. Вероятность, что канал свободен (доля времени простоя каналов). Следовательно, 52.6% в течение часа канал будет не занят, время простоя равно t_пр = 31.6 мин. Вероятность того, что обслуживанием: занят 1 канал: p₁ = ρ¹/1! p₀ = 0.9¹/1!*0.526 = 0.474

3. Определить математическое ожидание m(p) для пуассоновского потока заявок, если канал загружен на 65 процентов.

Вероятность р мала, а число n велико (np = 65 < 10). Значит случайная величина Х – распределена по Пуассоновскому распределению. Составим закон распределения. Случайная величина X имеет область значений (0,1,2,...,m). Вероятности этих значений можно найти по формуле: Найдем ряд распределения X. Здесь λ = np = 100*0.65 = 65 P(0) = e^{- λ} = e^-65 = 0 Математическое ожидание. M[X] = λ = 65

4.Определить значение времени интервала обслуживания заявок  для потока с интенсивностью 100 заявок в секунду, если система свободна от заявок 65 % времени.

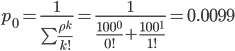1. Интенсивность нагрузки. Интенсивность нагрузки ρ=100 показывает степень согласованности входного и выходного потоков заявок канала обслуживания и определяет устойчивость системы массового обслуживания. 2. Время обслуживания (мин). 3. Вероятность, что канал свободен (доля времени простоя каналов). Следовательно, 0.99% в течение часа канал будет не занят, время простоя равно t_пр = 0.6 мин. Вероятность того, что обслуживанием: занят 1 канал: p₁ = ρ¹/1! p₀ = 100¹/1!*0.0099 = 0.99 4. Вероятность отказа (вероятность того, что канал занят) (доля заявок, получивших отказ). Значит, 99% из числа поступивших заявок не принимаются к обслуживанию. 5. Вероятность обслуживания поступающих заявок (вероятность того, что клиент будет обслужен). В системах с отказами события отказа и обслуживания составляют полную группу событий, поэтому: p_отк + p_обс = 1 Относительная пропускная способность: Q = p_обс. p_обс = 1 - p_отк = 1 - 0.99 = 0.0099 Следовательно, 1% из числа поступивших заявок будут обслужены. Приемлемый уровень обслуживания должен быть выше 90%. 6. Среднее число каналов, занятых обслуживанием (Среднее число занятых каналов). n_з = ρ*p_обс = 100*0.0099 = 0.99 канала. Среднее число простаивающих каналов. n_пр = n - n_з = 1 - 0.99 = 0 канала. 7. Коэффициент занятости каналов обслуживанием. Следовательно, система на 100% занята обслуживанием. 8. Абсолютная пропускная способность (Интенсивность выходящего потока обслуженных заявок). A = p_обс*λ = 0.0099*100 = 0.99 заявок/мин. 9. Среднее время простоя СМО ( мин.). t_пр = p_отк*t_обс = 0.99*1 = 0.99 10. Среднее время простоя канала ( мин.). t_п.к. = t_обс*(1-p_отк)/p_отк = 1*(1-0.99)/0.99 = 0.01 12. Среднее число обслуживаемых заявок. L_обс = ρ*Q = 100*0.0099 = 0.99 ед. 14. Среднее время пребывания заявки в СМО (формула Литтла). Число заявок, получивших отказ в течение часа: λ*p₁ = 99 заявок в мин. Номинальная производительность СМО: 1 / 1 = 1 заявок в мин. Фактическая производительность СМО: 0.99 / 1 = 99% от номинальной производительности.

5.* Определить средний размер очереди для пуассоновского потока с постоянным временем обслуживания, если система загружена на 65 % своего времени.

1. Интенсивность нагрузки. Интенсивность нагрузки ρ=153.846 показывает степень согласованности входного и выходного потоков заявок канала обслуживания и определяет устойчивость системы массового обслуживания. 2. Время обслуживания (мин). 3. Вероятность, что канал свободен (доля времени простоя каналов). 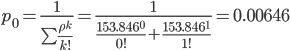Следовательно, 0.65% в течение часа канал будет не занят, время простоя равно t_пр = 0.4 мин. Вероятность того, что обслуживанием: занят 1 канал: p₁ = ρ¹/1! p₀ = 153.846¹/1!*0.00646 = 0.994 4. Вероятность отказа (вероятность того, что канал занят) (доля заявок, получивших отказ). Значит, 99% из числа поступивших заявок не принимаются к обслуживанию. 5. Вероятность обслуживания поступающих заявок (вероятность того, что клиент будет обслужен). В системах с отказами события отказа и обслуживания составляют полную группу событий, поэтому: p_отк + p_обс = 1 Относительная пропускная способность: Q = p_обс. p_обс = 1 - p_отк = 1 - 0.994 = 0.00646 Следовательно, 1% из числа поступивших заявок будут обслужены. Приемлемый уровень обслуживания должен быть выше 90%. 6. Среднее число каналов, занятых обслуживанием (Среднее число занятых каналов). n_з = ρ*p_обс = 153.846*0.00646 = 0.994 канала. Среднее число простаивающих каналов. n_пр = n - n_з = 1 - 0.994 = 0 канала. 7. Коэффициент занятости каналов обслуживанием. Следовательно, система на 100% занята обслуживанием. 8. Абсолютная пропускная способность (Интенсивность выходящего потока обслуженных заявок). A = p_обс*λ = 0.00646*100 = 0.646 заявок/мин. 9. Среднее время простоя СМО ( мин.). t_пр = p_отк*t_обс = 0.994*1.538 = 1.529 10. Среднее время простоя канала ( мин.). t_п.к. = t_обс*(1-p_отк)/p_отк = 1.538*(1-0.994)/0.994 = 0.00423 12. Среднее число обслуживаемых заявок. L_обс = ρ*Q = 153.846*0.00646 = 0.994 ед.

6. Определить средний размер очереди для пуассоновского потока с экспоненциальным временем обслуживания, если система загружена на 65% своего времени.

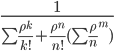1. Интенсивность нагрузки. Интенсивность нагрузки ρ=100 показывает степень согласованности входного и выходного потоков заявок канала обслуживания и определяет устойчивость системы массового обслуживания. 2. Время обслуживания (мин). 3. Вероятность, что канал свободен (доля времени простоя каналов).  =   =   =  Следовательно, 0.01% в течение часа канал будет не занят, время простоя равно t_пр = 0 мин. Вероятность того, что обслуживанием: занят 1 канал: p₁ = ρ¹/1! p₀ = 100¹/1!*9.9E-5 = 0.0099 4. Вероятность отказа (вероятность того, что канал занят) (доля заявок, получивших отказ). Значит, 99% из числа поступивших заявок не принимаются к обслуживанию. 5. Вероятность обслуживания поступающих заявок (вероятность того, что клиент будет обслужен). В системах с отказами события отказа и обслуживания составляют полную группу событий, поэтому: p_отк + p_обс = 1 Относительная пропускная способность: Q = p_обс. p_обс = 1 - p_отк = 1 - 0.99 = 0.01 Следовательно, 1% из числа поступивших заявок будут обслужены. Приемлемый уровень обслуживания должен быть выше 90%. 6. Среднее число каналов, занятых обслуживанием (Среднее число занятых каналов). n_з = ρ*p_обс = 100*0.01 = 1 канала. Среднее число простаивающих каналов. n_пр = n - n_з = 1 - 1 = 0 канала. 7. Коэффициент занятости каналов обслуживанием. Следовательно, система на 100% занята обслуживанием. 8. Абсолютная пропускная способность (Интенсивность выходящего потока обслуженных заявок). A = p_обс*λ = 0.01*65 = 0.65 заявок/мин. 9. Среднее время простоя СМО ( мин.). t_пр = p_отк*t_обс = 0.99*1.538 = 1.523 10. Среднее время простоя канала ( мин.). t_п.к. = t_обс*(1-p_отк)/p_отк = 1.538*(1-0.99)/0.99 = 0.00656 Вероятность образования очереди. Вероятность отсутствия очереди. p = 1 - p_оч = 1 - 9801 = -9800 10. Среднее число заявок, находящихся в очереди. 11. Среднее время простоя СМО (среднее время ожидания обслуживания заявки в очереди). 12. Среднее число обслуживаемых заявок. L_обс = ρ*Q = 100*0.01 = 1 ед. 13. Среднее число заявок в системе (т.е. заявки, которые уже обслуживаются, и те, которые еще стоят в очереди и ждут обслуживания). L_CMO = L_оч + L_обс = 0.99 + 1 = 1.99 ед. 14. Среднее время пребывания заявки в СМО. Число заявок, получивших отказ в течение часа: λ*p₁ = 64.35 заявок в мин. Номинальная производительность СМО: 1 / 1.538 = 0.65 заявок в мин. Фактическая производительность СМО: 0.65 / 0.65 = 100% от номинальной производительности.

7.* Определить время пребывания заявки в системе для пуассоновского потока с постоянным временем обслуживания, если система загружена на 65 % своего времени.

1. Интенсивность нагрузки. Интенсивность нагрузки ρ=123.077 показывает степень согласованности входного и выходного потоков заявок канала обслуживания и определяет устойчивость системы массового обслуживания. 2. Время обслуживания (мин). 3. Вероятность, что канал свободен (доля времени простоя каналов).  =   =   = 6.5E-5 Следовательно, 0.01% в течение часа канал будет не занят, время простоя равно t_пр = 0 мин. Вероятность того, что обслуживанием: занят 1 канал: p₁ = ρ¹/1! p₀ = 123.077¹/1!*6.5E-5 = 0.00806 4. Вероятность отказа (вероятность того, что канал занят) (доля заявок, получивших отказ). Значит, 99% из числа поступивших заявок не принимаются к обслуживанию. 5. Вероятность обслуживания поступающих заявок (вероятность того, что клиент будет обслужен). В системах с отказами события отказа и обслуживания составляют полную группу событий, поэтому: p_отк + p_обс = 1 Относительная пропускная способность: Q = p_обс. p_обс = 1 - p_отк = 1 - 0.992 = 0.00812 Следовательно, 1% из числа поступивших заявок будут обслужены. Приемлемый уровень обслуживания должен быть выше 90%. 6. Среднее число каналов, занятых обслуживанием (Среднее число занятых каналов). n_з = ρ*p_обс = 123.077*0.00812 = 1 канала. Среднее число простаивающих каналов. n_пр = n - n_з = 1 - 1 = 0 канала. 7. Коэффициент занятости каналов обслуживанием. Следовательно, система на 100% занята обслуживанием. 8. Абсолютная пропускная способность (Интенсивность выходящего потока обслуженных заявок). A = p_обс*λ = 0.00812*80 = 0.65 заявок/мин. 9. Среднее время простоя СМО ( мин.). t_пр = p_отк*t_обс = 0.992*1.538 = 1.526 10. Среднее время простоя канала ( мин.). t_п.к. = t_обс*(1-p_отк)/p_отк = 1.538*(1-0.992)/0.992 = 0.00532 Вероятность образования очереди. Вероятность отсутствия очереди. p = 1 - p_оч = 1 - 14902.775 = -14901.775 10. Среднее число заявок, находящихся в очереди. 11. Среднее время простоя СМО (среднее время ожидания обслуживания заявки в очереди). 12. Среднее число обслуживаемых заявок. L_обс = ρ*Q = 123.077*0.00812 = 1 ед. 13. Среднее число заявок в системе (т.е. заявки, которые уже обслуживаются, и те, которые еще стоят в очереди и ждут обслуживания). L_CMO = L_оч + L_обс = 0.992 + 1 = 1.992 ед. 14. Среднее время пребывания заявки в СМО. Число заявок, получивших отказ в течение часа: λ*p₁ = 79.36 заявок в мин. Номинальная производительность СМО: 1 / 1.538 = 0.65 заявок в мин. Фактическая производительность СМО: 0.65 / 0.65 = 100% от номинальной производительности.

8.* Определить вероятность того, что в системе с пуассоновским потоком отсутствуют заявки, если среднее число заявок в системе равно 0,7.

1. Интенсивность нагрузки. Интенсивность нагрузки ρ=114.286 показывает степень согласованности входного и выходного потоков заявок канала обслуживания и определяет устойчивость системы массового обслуживания. 2. Время обслуживания (мин). 3. Вероятность, что канал свободен (доля времени простоя каналов).  =   =   = 7.6E-5 Следовательно, 0.01% в течение часа канал будет не занят, время простоя равно t_пр = 0 мин. Вероятность того, что обслуживанием: занят 1 канал: p₁ = ρ¹/1! p₀ = 114.286¹/1!*7.6E-5 = 0.00867 4. Вероятность отказа (вероятность того, что канал занят) (доля заявок, получивших отказ). Значит, 99% из числа поступивших заявок не принимаются к обслуживанию. 5. Вероятность обслуживания поступающих заявок (вероятность того, что клиент будет обслужен). В системах с отказами события отказа и обслуживания составляют полную группу событий, поэтому: p_отк + p_обс = 1 Относительная пропускная способность: Q = p_обс. p_обс = 1 - p_отк = 1 - 0.991 = 0.00875 Следовательно, 1% из числа поступивших заявок будут обслужены. Приемлемый уровень обслуживания должен быть выше 90%. 6. Среднее число каналов, занятых обслуживанием (Среднее число занятых каналов). n_з = ρ*p_обс = 114.286*0.00875 = 1 канала. Среднее число простаивающих каналов. n_пр = n - n_з = 1 - 1 = 0 канала. 7. Коэффициент занятости каналов обслуживанием. Следовательно, система на 100% занята обслуживанием. 8. Абсолютная пропускная способность (Интенсивность выходящего потока обслуженных заявок). A = p_обс*λ = 0.00875*80 = 0.7 заявок/мин. 9. Среднее время простоя СМО ( мин.). t_пр = p_отк*t_обс = 0.991*1.429 = 1.416 10. Среднее время простоя канала ( мин.). t_п.к. = t_обс*(1-p_отк)/p_отк = 1.429*(1-0.991)/0.991 = 0.00618 Вероятность образования очереди. Вероятность отсутствия очереди. p = 1 - p_оч = 1 - 12833.653 = -12832.653 10. Среднее число заявок, находящихся в очереди. 11. Среднее время простоя СМО (среднее время ожидания обслуживания заявки в очереди). 12. Среднее число обслуживаемых заявок. L_обс = ρ*Q = 114.286*0.00875 = 1 ед. 13. Среднее число заявок в системе (т.е. заявки, которые уже обслуживаются, и те, которые еще стоят в очереди и ждут обслуживания). L_CMO = L_оч + L_обс = 0.991 + 1 = 1.991 ед. 14. Среднее время пребывания заявки в СМО. Число заявок, получивших отказ в течение часа: λ*p₁ = 79.28 заявок в мин. Номинальная производительность СМО: 1 / 1.429 = 0.7 заявок в мин. Фактическая производительность СМО: 0.7 / 0.7 = 100% от номинальной производительности.

9. Определить вероятность того, что в системе с пуассоновским потоком отсутствуют заявки, если в среднем в ней находится одна заявка.

1. Интенсивность нагрузки. ρ = λ*t_обс = 1*1 = 1 Интенсивность нагрузки ρ=1 показывает степень согласованности входного и выходного потоков заявок канала обслуживания и определяет устойчивость системы массового обслуживания. 3. Вероятность, что канал свободен (доля времени простоя каналов).

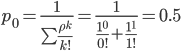
10. Определить вероятность того, что в системе с пуассоновским потоком находится одна заявка, если в среднем в ней находится одна заявка.

1. Интенсивность нагрузки. ρ = λ*t_обс = 1*1 = 1 Интенсивность нагрузки ρ=1 показывает степень согласованности входного и выходного потоков заявок канала обслуживания и определяет устойчивость системы массового обслуживания. 3. Вероятность, что канал свободен (доля времени простоя каналов). Следовательно, 50% в течение часа канал будет не занят, время простоя равно t_пр = 30 сек. Вероятность того, что обслуживанием: занят 1 канал: p₁ = ρ¹/1! p₀ = 1¹/1!*0.5 = 0.5

11. Определить вероятность того, что в системе с пуассоновским потоком находится хотя бы одна заявка, если в среднем в ней находится одна заявка.

Вероятность р мала, а число n велико (np = 100 < 10). Значит случайная величина Х – распределена по Пуассоновскому распределению. Составим закон распределения. Случайная величина X имеет область значений (0,1,2,...,m). Вероятности этих значений можно найти по формуле: Найдем ряд распределения X. Здесь λ = np = 100*1 = 100 P(0) = e^{- λ} = e^-100 = 0 Найдем вероятность того, что событие наступит хотя бы один раз. P(X > 0) = 1 - P(0) = 1 - 0 = 1

12.* Определить отношение двух безусловных вероятностей двух событий, если отношения их взаимных условных вероятностей равно 0,5

1. Интенсивность нагрузки. Интенсивность нагрузки ρ=200 показывает степень согласованности входного и выходного потоков заявок канала обслуживания и определяет устойчивость системы массового обслуживания. 2. Время обслуживания (мин). 3. Вероятность, что канал свободен (доля времени простоя каналов).  =   =   =  Следовательно, 0% в течение часа канал будет не занят, время простоя равно t_пр = 0 мин. Вероятность того, что обслуживанием: занят 1 канал: p₁ = ρ¹/1! p₀ = 200¹/1!*2.5E-5 = 0.00498 4. Вероятность отказа (вероятность того, что канал занят) (доля заявок, получивших отказ). Значит, 100% из числа поступивших заявок не принимаются к обслуживанию. 5. Вероятность отношения. В системах с отказами события отказа и обслуживания составляют полную группу событий, поэтому: p_отк + p_обс = 1 Относительная пропускная способность: Q = p_обс. p_обс = 1 - p_отк = 1 - 0.995 = 0.005 Следовательно, 1% из числа поступивших заявок будут обслужены. Приемлемый уровень обслуживания должен быть выше 90%.

13. Определить вероятность того, что интервал между заявками в пуассоновском потоке с интенсивностью 1 заявка в секунду, не больше одной секунды.

Вероятность р мала, а число n велико (np = 10 < 10). Значит случайная величина Х – распределена по Пуассоновскому распределению. Составим закон распределения. Случайная величина X имеет область значений (0,1,2,...,m). Вероятности этих значений можно найти по формуле: Найдем ряд распределения X. Здесь λ = np = 100*0.1 = 10 P(0) = e^{- λ} = e^-10 = 4.5 Найдем вероятность того, что событие наступит не более раз. P(X ≤ ) = 4.5

14.* Сообщения передаются парами бит. Определить вероятность передачи ошибочной пары, если вероятность ошибки при передаче каждого бита, равна 0,04.

1. Интенсивность нагрузки. Интенсивность нагрузки ρ=100 показывает степень согласованности входного и выходного потоков заявок канала обслуживания и определяет устойчивость системы массового обслуживания. 2. Время обслуживания (мин). 3. Вероятность, что канал свободен (доля времени простоя каналов). Следовательно, 0.99% в течение часа канал будет не занят, время простоя равно t_пр = 0.6 мин. Вероятность того, что обслуживанием: занят 1 канал: p₁ = ρ¹/1! p₀ = 100¹/1!*0.0099 = 0.99 4. Вероятность отказа (вероятность того, что канал занят) (доля заявок, получивших отказ). Значит, 99% из числа поступивших заявок не принимаются к обслуживанию. 5. Вероятность обслуживания поступающих заявок (вероятность того, что клиент будет обслужен). В системах с отказами события отказа и обслуживания составляют полную группу событий, поэтому: p_отк + p_обс = 1 Относительная пропускная способность: Q = p_обс. p_обс = 1 - p_отк = 1 - 0.99 = 0.0099 Следовательно, 1% из числа поступивших заявок будут обслужены. Приемлемый уровень обслуживания должен быть выше 90%. 6. Среднее число каналов, занятых обслуживанием (Среднее число занятых каналов). n_з = ρ*p_обс = 100*0.0099 = 0.99 канала. Среднее число простаивающих каналов. n_пр = n - n_з = 1 - 0.99 = 0 канала. 7. Коэффициент занятости каналов обслуживанием. Следовательно, система на 100% занята обслуживанием. 8. Абсолютная пропускная способность (Интенсивность выходящего потока обслуженных заявок). A = p_обс*λ = 0.0099*100 = 0.99 заявок/мин. 9. Среднее время простоя СМО ( мин.). t_пр = p_отк*t_обс = 0.99*1 = 0.99 10. Среднее время простоя канала ( мин.). t_п.к. = t_обс*(1-p_отк)/p_отк = 1*(1-0.99)/0.99 = 0.01 12. Среднее число обслуживаемых заявок. L_обс = ρ*Q = 100*0.0099 = 0.99 ед. 14. Среднее время пребывания заявки в СМО (формула Литтла). Число заявок, получивших отказ в течение часа: λ*p₁ = 99 заявок в мин. Номинальная производительность СМО: 1 / 1 = 1 заявок в мин. Фактическая производительность СМО: 0.99 / 1 = 99% от номинальной производительности.

15.Определить вероятность нахождения в системе M/M/1/  одной заявки, если загрузка системы равна 0,9

. 1. Интенсивность нагрузки. Интенсивность нагрузки ρ=111.111 показывает степень согласованности входного и выходного потоков заявок канала обслуживания и определяет устойчивость системы массового обслуживания. 2. Время обслуживания (мин). 3. Вероятность, что канал свободен (доля времени простоя каналов). 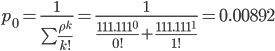Следовательно, 0.89% в течение часа канал будет не занят, время простоя равно t_пр = 0.5 мин. Вероятность того, что обслуживанием: занят 1 канал: p₁ = ρ¹/1! p₀ = 111.111¹/1!*0.00892 = 0.991 4. Вероятность отказа (вероятность того, что канал занят) (доля заявок, получивших отказ). Значит, 99% из числа поступивших заявок не принимаются к обслуживанию. 5. Вероятность обслуживания поступающих заявок (вероятность того, что клиент будет обслужен). В системах с отказами события отказа и обслуживания составляют полную группу событий, поэтому: p_отк + p_обс = 1 Относительная пропускная способность: Q = p_обс. p_обс = 1 - p_отк = 1 - 0.991 = 0.00892 Следовательно, 1% из числа поступивших заявок будут обслужены. Приемлемый уровень обслуживания должен быть выше 90%. 6. Среднее число каналов, занятых обслуживанием (Среднее число занятых каналов). n_з = ρ*p_обс = 111.111*0.00892 = 0.991 канала. Среднее число простаивающих каналов. n_пр = n - n_з = 1 - 0.991 = 0 канала. 7. Коэффициент занятости каналов обслуживанием. Следовательно, система на 100% занята обслуживанием. 8. Абсолютная пропускная способность (Интенсивность выходящего потока обслуженных заявок). A = p_обс*λ = 0.00892*100 = 0.892 заявок/мин. 9. Среднее время простоя СМО ( мин.). t_пр = p_отк*t_обс = 0.991*1.111 = 1.101 10. Среднее время простоя канала ( мин.). t_п.к. = t_обс*(1-p_отк)/p_отк = 1.111*(1-0.991)/0.991 = 0.0081 12. Среднее число обслуживаемых заявок. L_обс = ρ*Q = 111.111*0.00892 = 0.991 ед. 14. Среднее время пребывания заявки в СМО (формула Литтла). Число заявок, получивших отказ в течение часа: λ*p₁ = 99.1 заявок в мин. Номинальная производительность СМО: 1 / 1.111 = 0.9 заявок в мин. Фактическая производительность СМО: 0.892 / 0.9 = 99% от номинальной производительности.

16. Определить вероятность блокировки системы M/M/1/N, если N равно 1, а загрузка системы равна 0,9 .

1. Интенсивность нагрузки. Интенсивность нагрузки ρ=111.111 показывает степень согласованности входного и выходного потоков заявок канала обслуживания и определяет устойчивость системы массового обслуживания. 2. Время обслуживания (мин). 3. Вероятность, что канал свободен (доля времени простоя каналов). Следовательно, 0.89% в течение часа канал будет не занят, время простоя равно t_пр = 0.5 мин. Вероятность того, что обслуживанием: занят 1 канал: p₁ = ρ¹/1! p₀ = 111.111¹/1!*0.00892 = 0.991 4. Вероятность отказа (вероятность того, что канал занят) (доля заявок, получивших отказ). Значит, 99% из числа поступивших заявок не принимаются к обслуживанию.

17. Определить среднее число заявок в системе M/M/1/  , если она простаивает 65% времени.

1. Интенсивность нагрузки. ρ = λ*t_обс = 1*0.65 = 0.65 Интенсивность нагрузки ρ=0.65 показывает степень согласованности входного и выходного потоков заявок канала обслуживания и определяет устойчивость системы массового обслуживания. 3. Вероятность, что канал свободен (доля времени простоя каналов). 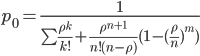 =  = 0.522 Следовательно, 52.2% в течение часа канал будет не занят, время простоя равно t_пр = 31.3 мин. Вероятность того, что обслуживанием: занят 1 канал: p₁ = ρ¹/1! p₀ = 0.65¹/1!*0.522 = 0.339 заняты 2 канала: p₂ = ρ²/2! p₀ = 0.65²/2!*0.522 = 0.11 заняты 3 канала: p₃ = ρ³/3! p₀ = 0.65³/3!*0.522 = 0.0239 заняты 4 канала: p₄ = ρ⁴/4! p₀ = 0.65⁴/4!*0.522 = 0.00388 заняты 5 канала: p₅ = ρ⁵/5! p₀ = 0.65⁵/5!*0.522 = 0.000505 заняты 6 канала: p₆ = ρ⁶/6! p₀ = 0.65⁶/6!*0.522 = 5.5E-5 заняты 7 канала: p₇ = ρ⁷/7! p₀ = 0.65⁷/7!*0.522 = 5.0E-6 4. Вероятность отказа (вероятность того, что канал занят) (доля заявок, получивших отказ). Заявки не получают отказ. Обслуживаются все поступившие заявки. 5. Вероятность обслуживания поступающих заявок (вероятность того, что клиент будет обслужен). В системах с отказами события отказа и обслуживания составляют полную группу событий, поэтому: p_отк + p_обс = 1 Относительная пропускная способность: Q = p_обс. p_обс = 1 - p_отк = 1 - 0 = 1 Следовательно, 100% из числа поступивших заявок будут обслужены. Приемлемый уровень обслуживания должен быть выше 90%. 6. Среднее число каналов, занятых обслуживанием (Среднее число занятых каналов). n_з = ρ*p_обс = 0.65*1 = 0.65 канала. Среднее число простаивающих каналов. n_пр = n - n_з = 20 - 0.65 = 19.4 канала. 7. Коэффициент занятости каналов обслуживанием. Следовательно, система на 0% занята обслуживанием. 8. Абсолютная пропускная способность (Интенсивность выходящего потока обслуженных заявок). A = p_обс*λ = 1*1 = 1 заявок/мин. 9. Среднее время простоя СМО ( мин.). t_пр = p_отк*t_обс = 0*0.65 = 0 10. Среднее время простоя канала ( мин.). t_п.к. = t_обс*(1-p_отк)/p_отк = 0.65*(1-0)/0 = 1.2171726345401E+24 Вероятность образования очереди. Вероятность отсутствия очереди. p = 1 - p_оч = 1 - 0 = 1 10. Среднее число заявок, находящихся в очереди. 11. Среднее время простоя СМО (среднее время ожидания обслуживания заявки в очереди). 12. Среднее число обслуживаемых заявок. L_обс = ρ*Q = 0.65*1 = 0.65 ед. 13. Среднее число заявок в системе (т.е. заявки, которые уже обслуживаются, и те, которые еще стоят в очереди и ждут обслуживания). L_CMO = L_оч + L_обс = 0 + 0.65 = 0.65 ед.

18. Определить среднее число заявок в системе с загрузкой, равной 0,9, если в очереди находится 2 заявки.

Интенсивность потока обслуживания: 1. Интенсивность нагрузки. ρ = λ*t_обс = 2*0.9 = 1.8 Интенсивность нагрузки ρ=1.8 показывает степень согласованности входного и выходного потоков заявок канала обслуживания и определяет устойчивость системы массового обслуживания. 3. Вероятность, что канал свободен (доля времени простоя каналов).  =  = 0.165 Следовательно, 16.5% в течение часа канал будет не занят, время простоя равно t_пр = 9.9 мин. Вероятность того, что обслуживанием: занят 1 канал: p₁ = ρ¹/1! p₀ = 1.8¹/1!*0.165 = 0.298 заняты 2 канала: p₂ = ρ²/2! p₀ = 1.8²/2!*0.165 = 0.268 заняты 3 канала: p₃ = ρ³/3! p₀ = 1.8³/3!*0.165 = 0.161 заняты 4 канала: p₄ = ρ⁴/4! p₀ = 1.8⁴/4!*0.165 = 0.0723 заняты 5 канала: p₅ = ρ⁵/5! p₀ = 1.8⁵/5!*0.165 = 0.026 заняты 6 канала: p₆ = ρ⁶/6! p₀ = 1.8⁶/6!*0.165 = 0.00781 заняты 7 канала: p₇ = ρ⁷/7! p₀ = 1.8⁷/7!*0.165 = 0.00201 заняты 8 канала: p₈ = ρ⁸/8! p₀ = 1.8⁸/8!*0.165 = 0.000452 заняты 9 канала: p₉ = ρ⁹/9! p₀ = 1.8⁹/9!*0.165 = 9.0E-5 заняты 10 канала: p₁₀ = ρ¹⁰/10! p₀ = 1.8¹⁰/10!*0.165 = 1.6E-5 заняты 11 канала: p₁₁ = ρ¹¹/11! p₀ = 1.8¹¹/11!*0.165 = 3.0E-6 4. Вероятность отказа (вероятность того, что канал занят) (доля заявок, получивших отказ). Заявки не получают отказ. Обслуживаются все поступившие заявки. 5. Вероятность обслуживания поступающих заявок (вероятность того, что клиент будет обслужен). В системах с отказами события отказа и обслуживания составляют полную группу событий, поэтому: p_отк + p_обс = 1 Относительная пропускная способность: Q = p_обс. p_обс = 1 - p_отк = 1 - 0 = 1 Следовательно, 100% из числа поступивших заявок будут обслужены. Приемлемый уровень обслуживания должен быть выше 90%. 6. Среднее число каналов, занятых обслуживанием (Среднее число занятых каналов). n_з = ρ*p_обс = 1.8*1 = 1.8 канала. Среднее число простаивающих каналов. n_пр = n - n_з = 20 - 1.8 = 18.2 канала. 7. Коэффициент занятости каналов обслуживанием. Следовательно, система на 10% занята обслуживанием. 8. Абсолютная пропускная способность (Интенсивность выходящего потока обслуженных заявок). A = p_обс*λ = 1*2 = 2 заявок/мин. 9. Среднее время простоя СМО ( мин.). t_пр = p_отк*t_обс = 0*0.9 = 0 10. Среднее время простоя канала ( мин.). t_п.к. = t_обс*(1-p_отк)/p_отк = 0.9*(1-0)/0 = 1.5837150867982E+16 Вероятность образования очереди. Вероятность отсутствия очереди. p = 1 - p_оч = 1 - 0 = 1 10. Среднее число заявок, находящихся в очереди. 11. Среднее время простоя СМО (среднее время ожидания обслуживания заявки в очереди). 12. Среднее число обслуживаемых заявок. L_обс = ρ*Q = 1.8*1 = 1.8 ед. 13. Среднее число заявок в системе (т.е. заявки, которые уже обслуживаются, и те, которые еще стоят в очереди и ждут обслуживания). L_CMO = L_оч + L_обс = 0 + 1.8 = 1.8 ед.

19.* Определить среднее время задержки в системе m/m/2/  , если среднее время обработки одной заявки равно 0,1 секунды, а загрузка системы равна 0,9.

Интенсивность потока обслуживания: 1. Интенсивность нагрузки. ρ = λ*t_обс = 0.9*0.1 = 0.09 Интенсивность нагрузки ρ=0.09 показывает степень согласованности входного и выходного потоков заявок канала обслуживания и определяет устойчивость системы массового обслуживания. 3. Вероятность, что канал свободен (доля времени простоя каналов).  =  = 0.914 Следовательно, 91.4% в течение часа канал будет не занят, время простоя равно t_пр = 54.8 мин. Вероятность того, что обслуживанием: занят 1 канал: p₁ = ρ¹/1! p₀ = 0.09¹/1!*0.914 = 0.0823 заняты 2 канала: p₂ = ρ²/2! p₀ = 0.09²/2!*0.914 = 0.0037 заняты 3 канала: p₃ = ρ³/3! p₀ = 0.09³/3!*0.914 = 0.000111 заняты 4 канала: p₄ = ρ⁴/4! p₀ = 0.09⁴/4!*0.914 = 2.0E-6 4. Вероятность отказа (вероятность того, что канал занят) (доля заявок, получивших отказ). Заявки не получают отказ. Обслуживаются все поступившие заявки. 5. Вероятность обслуживания поступающих заявок (вероятность того, что клиент будет обслужен). В системах с отказами события отказа и обслуживания составляют полную группу событий, поэтому: p_отк + p_обс = 1 Относительная пропускная способность: Q = p_обс. p_обс = 1 - p_отк = 1 - 0 = 1 Следовательно, 100% из числа поступивших заявок будут обслужены. Приемлемый уровень обслуживания должен быть выше 90%. 6. Среднее число каналов, занятых обслуживанием (Среднее число занятых каналов). n_з = ρ*p_обс = 0.09*1 = 0.09 канала. Среднее число простаивающих каналов. n_пр = n - n_з = 20 - 0.09 = 19.9 канала. 7. Коэффициент занятости каналов обслуживанием. Следовательно, система на 0% занята обслуживанием. 8. Среднее врем задержки A = p_обс*λ = 1*0.9 = 0.9 заявок/мин.

19. Определить среднее время задержки в системе m/m/2/  , если среднее время обработки одной заявки равно 0,1 секунды, а загрузка системы равна 0,9.

Интенсивность потока обслуживания: 1. Интенсивность нагрузки. ρ = λ*t_обс = 0.9*0.1 = 0.09 Интенсивность нагрузки ρ=0.09 показывает степень согласованности входного и выходного потоков заявок канала обслуживания и определяет устойчивость системы массового обслуживания. 3. Вероятность, что канал свободен (доля времени простоя каналов). 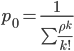 =  = 0.914 Следовательно, 91.4% в течение часа канал будет не занят, время простоя равно t_пр = 54.8 мин. Вероятность того, что обслуживанием: занят 1 канал: p₁ = ρ¹/1! p₀ = 0.09¹/1!*0.914 = 0.0823 заняты 2 канала: p₂ = ρ²/2! p₀ = 0.09²/2!*0.914 = 0.0037 заняты 3 канала: p₃ = ρ³/3! p₀ = 0.09³/3!*0.914 = 0.000111 заняты 4 канала: p₄ = ρ⁴/4! p₀ = 0.09⁴/4!*0.914 = 2.0E-6 Заявки не получают отказ. Обслуживаются все поступившие заявки. Вероятность обслуживания поступающих заявок (вероятность того, что клиент будет обслужен). В системах с отказами события отказа и обслуживания составляют полную группу событий, поэтому: p_отк + p_обс = 1 Относительная пропускная способность: Q = p_обс. p_обс = 1 - p_отк = 1 - 0 = 1 Следовательно, 100% из числа поступивших заявок будут обслужены. Приемлемый уровень обслуживания должен быть выше 90%. Среднее число каналов, занятых обслуживанием (Среднее число занятых каналов). n_з = ρ*p_обс = 0.09*1 = 0.09 канала. Среднее число простаивающих каналов. n_пр = n - n_з = 20 - 0.09 = 19.9 канала. Следовательно, система на 0% занята обслуживанием. Абсолютная пропускная способность (Интенсивность выходящего потока обслуженных заявок). A = p_обс*λ = 1*0.9 = 0.9 заявок/мин. . Среднее время простоя канала ( мин.). t_п.к. = t_обс*(1-p_отк)/p_отк = 0.1*(1-0)/0 = 2.1895805745654E+40 Среднее число обслуживаемых заявок. L_обс = ρ*Q = 0.09*1 = 0.09 ед. 14. Среднее время пребывания заявки в СМО (формула Литтла). Число заявок, получивших отказ в течение часа: λ*p₁ = 0 заявок в мин. Номинальная производительность СМО: 20 / 0.1 = 200 заявок в мин.