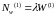ТМС 2 курс 2 семестр / Ответы по ТМС
.docxОтветы к ТМС
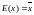 это
математическое ожидание -так обозначается
здесь
это
математическое ожидание -так обозначается
здесь
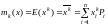 начальный
момент k-го
порядка - так обозначается здесь.
начальный
момент k-го
порядка - так обозначается здесь.
1.Определение вероятности и основные соотношения ВЕРОЯТНОСТЬ – показатель осуществимости тех или иных возможностей при определенных условиях Свойства вероятности:
Вероятность достоверного события равна единице.
Вероятность невозможного события равна нулю. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.
2.Вероятности
событий. Независимые события.
Вероятность события –
это отношение частоты появления
некоторого события к общему числу
событий.
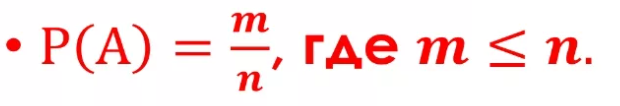
3.Условные вероятности. Условной вероятностью PA(B)=P(B|A) (два обозначения) называют вероятность события ВВ, вычисленную в предположении, что событие АА уже наступило.
Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность второго, вычисленную при условии, что первое событие произошло, т.е.
P(AB)=P(B)⋅P(A|B)=P(A)⋅P(B|A).
В частности, отсюда получаем формулы для условной вероятности:
P(A|B)=P(AB)/P(B), P(B|A)=P(AB)/P(A).
4.Формула
Байса По формуле
Байеса можно
более точно пересчитать вероятность,
беря в расчет как ранее известную
информацию, так и данные новых наблюдений.
Формула Байеса позволяет «переставить
причину и следствие»:
по известному факту события вычислить
вероятность того, что оно было вызвано
данной причиной. События, отражающие
действие «причин», в данном случае
называют гипотезами, так как они
—предполагаемые события, повлекшие
данное.
По формуле
Байеса можно
более точно пересчитать вероятность,
беря в расчет как ранее известную
информацию, так и данные новых наблюдений.
Формула Байеса позволяет «переставить
причину и следствие»:
по известному факту события вычислить
вероятность того, что оно было вызвано
данной причиной. События, отражающие
действие «причин», в данном случае
называют гипотезами, так как они
—предполагаемые события, повлекшие
данное.
5.Случайные величины непрерывные и дискретные Случайные величины обычно делят на дискретные и непрерывные. Дискретный или непрерывный характер случайной величины определяется объективными свойствами исследуемого процесса. Для проведения анализа некоторых СМО целесообразно переходить от непрерывных случайных величин к дискретным или наоборот
6
Интегральная функция распределения
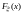 Интегральная функция распределения
позволяет задать как дискретную, так и
непрерывную случайную величину.
Интегральная функция распределения
позволяет задать как дискретную, так и
непрерывную случайную величину.
Интегральная функция распределения
(ИФР)– это функция F(x),
определяющая для каждого возможного
значения x вероятность того,
что случайная
величина X примет значение меньшее x,
т. е.
![]() Свойства
интегральной функции распределения:
Свойства
интегральной функции распределения:
Значения
интегральной функции распределения
принадлежат отрезку [0;1]: ![]() ..
..
Вероятность того, что случайная величина X примет значение, заключенной в интервале (a,b), равна приращению интегральной функции распределения на этом интервале
![]()
Если все возможные значения x случайной величины принадлежат интервалу (a, b), то
![]() ,
если
,
если ![]() ,
,
![]() ,
если
,
если ![]() .
.
7.Распределение
вероятностей дискретной величины Закон
распределения дискретной случайной
величины это соответствие между
возможными значениями и вероятностями,
с которыми эти значения принимает
случайная величина
Закон
распределения дискретной случайной
величины это соответствие между
возможными значениями и вероятностями,
с которыми эти значения принимает
случайная величина
8.Плотность
распределения непрерывной случайной
величины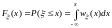
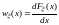
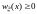 Плотность
вероятности — это производная от функции
F(x), описывающей распределение случайной
величины.
Плотность
распределения обладает следующими
свойствами:
Плотность
вероятности — это производная от функции
F(x), описывающей распределение случайной
величины.
Плотность
распределения обладает следующими
свойствами:
Интеграл от плотности равен единице по всему пространству: ∫∞−∞f(x)dx=1∫−∞∞f(x)dx=1. Выражение f(x)dxf(x)dx называют элементом вероятности.
Плотность распределения выполняется почти всюду, множество, на котором функция не будет выполнена, имеет меру ноль. Отрицательной плотность быть не может.
Вероятность попадания непрерывной случайной величины в промежуток [a,b][a,b] равна определенному интегралу от ее плотности в пределах этого промежутка.
9.Числовые характеристики случайных величин Числовыми характеристиками случайной величины являются ее математическое ожидание, имеющее смысл среднего значения, и дисперсия, характеризующая разброс значений случайной величины относительно ее математического ожидания.
10.Математические
моменты
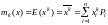 Момент случайной
величины — числовая характеристика
распределения данной случайной
величины
Есть
К момент случайный величины - начальный,
центральный, абсолютно центральный и
факториальный
Момент случайной
величины — числовая характеристика
распределения данной случайной
величины
Есть
К момент случайный величины - начальный,
центральный, абсолютно центральный и
факториальный
11.Математическое
ожидание
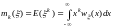 Математическим
ожиданием случайной величины называется
сумма произведений всех возможных
значений случайной величины на вероятности
этих значений
Математическим
ожиданием случайной величины называется
сумма произведений всех возможных
значений случайной величины на вероятности
этих значений
12.Свойства
математического ожидания
Свойство
1. Математическое
ожидание постоянной
величины равно самой постоянной:![]() .
Свойство
2. Постоянный
множитель можно выносить за знак
математического ожидания
.
Свойство
2. Постоянный
множитель можно выносить за знак
математического ожидания
![]() .
Свойство
3. Математическое
ожидание произведения двух независимых
случайных величин равно произведению
их математических ожиданий:
.
Свойство
3. Математическое
ожидание произведения двух независимых
случайных величин равно произведению
их математических ожиданий: ![]() Свойство
4. Математическое
ожидание суммы двух случайных величин
равно сумме математических ожиданий
слагаемых
Свойство
4. Математическое
ожидание суммы двух случайных величин
равно сумме математических ожиданий
слагаемых
![]() .
.
13.Центрированная величина Центрированная случайная величина – это разность между данной случайной величиной и ее математическим ожиданием Центрированной случайной величиной называется случайная величина, математическое ожидание которой находится в начале координат (в центре числовой оси).
14.Второй
начальный момент.
Дисперсия.
Второй начальный момент случайной
величины равен сумме второй и
первой производных производящей
функции
Дисперсия
случайной величины –
 характеризует меру рассеяния случайной
величины. Она рассчитывается как
математическое ожидание квадрата
отклонения случайной величины от своего
среднего значения:
характеризует меру рассеяния случайной
величины. Она рассчитывается как
математическое ожидание квадрата
отклонения случайной величины от своего
среднего значения:

16.Потоки событий. Определения Поток событий — Поток событий [flow of events] последовательность однородных событий, следующих одно за другим в случайные моменты времени (в предельном случае, если события следуют через определенные интервалы, П.с. называется регулярным)
17.Однородный, регулярный, Стационарный, Простейший потоки. Поток однородных событий — случайная последовательность событий, упорядоченных по неубыванию моментов времени. Регулярный поток – события происходят через равный промежуток времени Стационарный поток – это такой поток, в каждой фиксированной точке пространства которого не изменяются во времени параметры, влияющие на движение жидкости (вязкость, температура, давление, скорость и т.д.). Для стационарного потока вероятность поступления k заявок за некий промежуток времени от точки a до точки b зависит только от величины (b-a).
18.Интенсивность
ординарного потока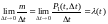 Таким
образом, интенсивность потока –
это вероятность появления одного события
на бесконечно малом промежутке времени.
На практике интенсивность замеряют
на некотором конечном промежутке времени
и она приводится к этому промежутку.
Таким
образом, интенсивность потока –
это вероятность появления одного события
на бесконечно малом промежутке времени.
На практике интенсивность замеряют
на некотором конечном промежутке времени
и она приводится к этому промежутку.
19.Пуассоновский
поток
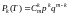 Пуассоновским
потоком называют ординарный поток
заявок с отсутствием последействия, у
которых количество заявок, поступающих
в систему за промежуток времени t распределено
по закону Пуассона:
Пуассоновским
потоком называют ординарный поток
заявок с отсутствием последействия, у
которых количество заявок, поступающих
в систему за промежуток времени t распределено
по закону Пуассона:
 где Р(k,t) -
вероятность того, что за время t в
систему поступит ровно k заявок
где Р(k,t) -
вероятность того, что за время t в
систему поступит ровно k заявок
λ - интенсивность потока
20.Среднее
значение пуассоноаского потока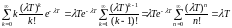
21.Дисперсия
пуассоновского потока
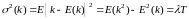 .
.
22.Экспоненциальное
распределение
интервалов
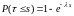
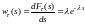 Экспоненциальное (или показательное) распределение —
абсолютно непрерывное распределение,
моделирующее время между двумя
последовательными свершениями одного
и того же события.
Экспоненциальное (или показательное) распределение —
абсолютно непрерывное распределение,
моделирующее время между двумя
последовательными свершениями одного
и того же события.
23.Матиматическое ожидание и дисперсия экспоненциального распределения интервалов

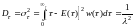
24.Классификация
систем массового обслуживания.
Элементы.
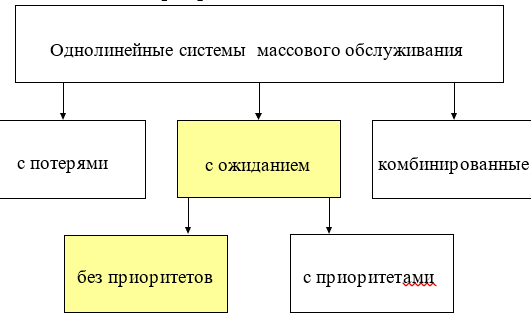 Элементами СМО являются:
входной (входящий) поток требований
(заявок) на обслуживание; приборы
(каналы) обслуживания
Элементами СМО являются:
входной (входящий) поток требований
(заявок) на обслуживание; приборы
(каналы) обслуживания
25.Система
М/М/1/∞ 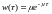 Экспоненциальное
распределение с параметром м
Экспоненциальное
распределение с параметром м
26.Система
М/М/1/∞ Уравнение равновесия.
![]() Это
уравнение равновесия. Левая часть
описывает уходы из состояния n,
правая – приходы в состояние n.
Это
уравнение равновесия. Левая часть
описывает уходы из состояния n,
правая – приходы в состояние n.
27.Система
М/М/1/∞
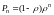

28Среднее
число заявок в системе М/М/1/∞


29.Среднее
число заявок в очереди М/М/1/∞

30.
Формула Литтла
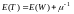

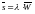 Формула
Литтла
связывает величину
Формула
Литтла
связывает величину
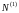 ,
интенсивность пуассоновского потока
заявок
,
интенсивность пуассоновского потока
заявок
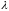 и время их задержки (ожидание плюс
обслуживание) в системе
и время их задержки (ожидание плюс
обслуживание) в системе
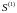
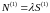 Иногда
формулу Литтла записывают в иной
редакции. Если
Иногда
формулу Литтла записывают в иной
редакции. Если
 и
и
W (1) обозначают средние значения длины очереди и длительности ожидания, то справедливо следующее соотношение: