
Word / Word_Вариант_2
.pdf
ФГБОУ ВПО Уфимский государственный авиационный технический университет
Кафедра Информатики
100 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
90
80
70
60
50
40
30
20
10
Выполнение индивидуального задания
в MS Word
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
к лабораторной работе по информатике
1308.5011ХХ.000ПЗ
(обозначение документа)
|
|
|
|
|
|
|
|
|
Группа |
|
ХХХ |
|
Фамилия, И., О. |
Подпись |
Дата |
Оценка |
|
|
|
|
|
|
|
|
|
|
Студент |
|
|
ХХХХХХХХХ |
|
|
|
||
|
|
|
|
|
|
|
||
Консультант |
|
|
ХХХХХХХХХ |
|
|
|
||
|
|
|
|
|
|
|
||
Принял |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Уфа 2012 г.

|
Содержание |
|
Введение............................................................................................................. |
3 |
|
1 |
Численное интегрирование...................................................................... |
4 |
1.1 |
Интегрирование по методу правых прямоугольников........................ |
4 |
1.2 |
Алгоритм метода правых прямоугольников......................................... |
5 |
Заключение ........................................................................................................ |
7 |
|
Список литературы ........................................................................................... |
8 |
|
|
|
|
|
1308.5011ХХ.000ПЗ |
||||||
|
|
|
|
|||||||
Изм. |
|
№ докум. Подп. |
|
|||||||
Лист |
Дата |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
Разраб. |
ФИО студента |
|
|
Лит. |
|
Лист |
Листов |
|||
|
|
|
|
|
|
|
|
|
|
|
Пров. |
|
|
Выполнение индивидуального задания в |
|
Д |
|
|
|
8 |
|
Рецен. |
|
|
MS Word |
|
|
|
||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
УГАТУ ХХХ 1 |
||
Н контр |
ФИО препод. |
|
|
|
|
|
||||
. . |
|
|
|
|
|
|
|
|
||
Утв. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Стиль Заголовок 1 |
|
|
|
||
|
Введение |
|
|
|
|
|
|
|
|
|
Инженеру часто приходится вычислять значения определенного интеграла: |
||||||||
при анализе инженерных и научных данных, для оценки показателей качества |
|||||||||
работы технических объектов и систем, входные и выходные переменные |
|||||||||
которых изменяются во времени или пространстве и др. |
Стиль Основной_ПЗ |
||||||||
|
Пусть |
дана функция |
f ( x) , которая непрерывна на интервале |
[a, b] и |
|||||
определена ее первообразная F ( x) , тогда определенный интеграл |
можно |
||||||||
вычислить по формуле Ньютона-Лейбница |
|
|
|
|
|||||
|
|
|
b |
|
|
|
|
Название |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ f ( x)dx = F (b) − F (a) , |
|
|
(1) |
|||
|
|
|
a |
|
|
|
|
|
|
где |
′ |
|
|
|
|
|
|
|
|
F ( x) = f ( x) . |
|
|
|
|
|
|
|
||
Пример. Рассчитать |
нагрев |
медного проводника |
за |
указанный промежуток |
|||||
времени при изменяющейся силе тока. |
|
|
|
|
|||||
|
При протекании электрического тока по проводнику, в нем выделяется |
||||||||
энергия. За время с момента t0 до tk |
в проводнике выделится энергия: |
|
|||||||
|
|
|
|
t k |
I 2 (t )R(t )dt , |
|
|
|
|
|
|
|
|
W = ∫ |
|
|
(2) |
||
|
|
|
|
t0 |
|
|
|
|
|
где I(t) – закон изменения силы тока в цепи. Если считать, что сопротивление R(t) |
|||||||||
не зависит от времени, его можно вынести за знак интеграла: |
|
||||||||
|
|
|
|
|
t k |
|
|
|
|
|
|
|
|
W = R ∫ I 2 (t ) |
dt |
|
|
(3) |
|
|
|
|
|
|
t 0 |
|
|
|
|
Изм. |
№ докум. |
Подп. |
Дата |
|
|
|
|
|
3 |
|
|
|
|
|
|
||||
1 Численное интегрирование 

Стиль Заголовок 1
На практике чаще встречаются интегралы, которые невозможно вычислить по формуле (1). В этом случае приходится прибегать к приближенному
вычислению интегралов численными методами [1]. |
|
|
|
Перекрестная ссылка |
|||
|
|
|
|||||
|
Интегрирование численными методами предполагает, что интервал |
||||||
интегрирования [a, b] делится точками x0 , x1,K, xn |
на n равных частей, причем |
||||||
x |
= a, x |
|
= b , длина каждой части составляет |
h = |
b − a |
. Из каждой точки |
|
n |
|
|
|||||
0 |
|
|
|
n |
|||
|
|
|
|
|
|||
xi |
= x0 + i h, i = 1,K, n − 1 проводится перпендикуляр до пересечения с кривой |
||||||
y = f ( x) , получается, что большая криволинейная трапеция разбивается на n
маленьких. |
Стиль Заголовок 2 |
|
1.1 Интегрирование по методу правых прямоугольников
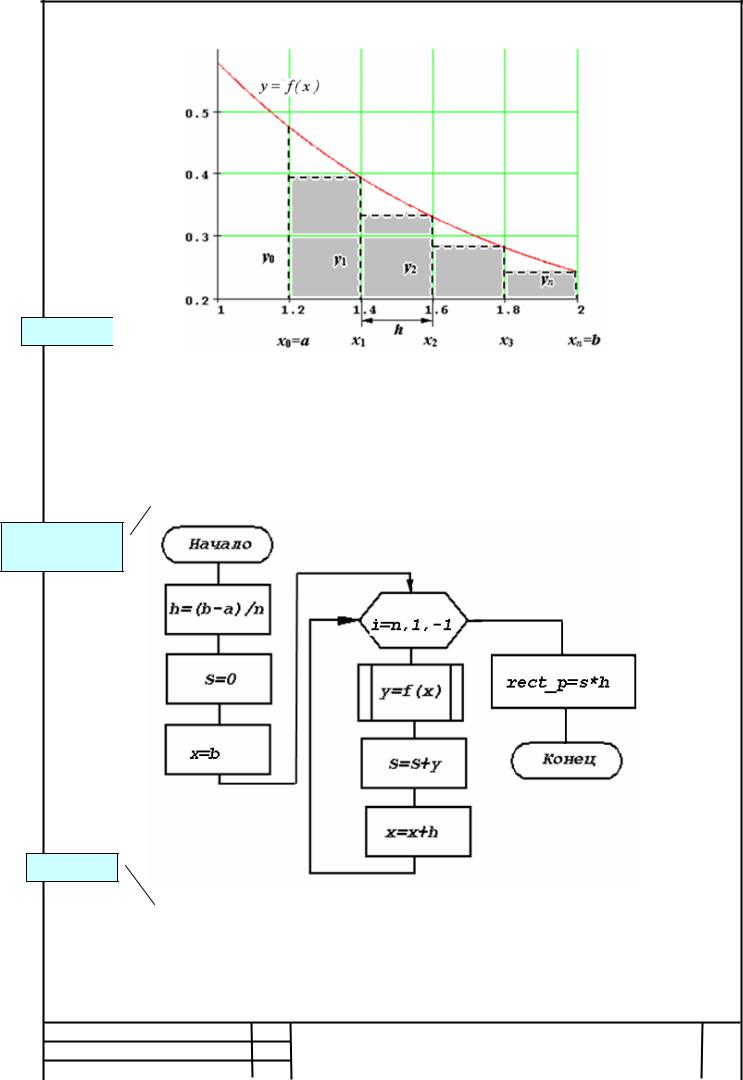
Идея численного интегрирования методом прямоугольников заключается в том, что для каждой маленькой трапеции отрезок кривой подинтегральной функции заменяется прямой параллельной оси абсцисс, т.е. маленькая криволинейная трапеция заменяется прямоугольником. Площадь полученной фигуры можно найти как сумму площадей прямоугольников, стороны которых равны h и yi.. Площадь отдельного прямоугольника составит Si = yi h .
Для метода правых прямоугольников построение начинается с права на лево
(рисунок 1.1), т.е. от точки xn до точки x1 тогда
|
b |
Перекрестная |
S = ∫ f ( x)dx = y1h + L + y n h = h ( f ( x1 ) + L + f ( xn )) . |
ссылка |
a |
|
Формулу численного вычисления определенного интеграла можно записать в виде
b |
n |
|
I = ∫ f ( x)dx ≈ h ∑ f ( xi ) . |
(1.1) |
|
a |
i=1 |
|
|
|
|
|
|
|
|
Изм. |
|
№ докум. |
Подп. |
Дата |
4 |
|
|
|
|
Название 

Рисунок 1.1 – Графическая интерпретация метода правых прямоугольников
1.2 Алгоритм метода правых прямоугольников
Алгоритм метода правых прямоугольников представлен блок-схемой
(рисунок 1.2).
Перекрестная
ссылка
Название
Рисунок 1.2 – Блок-схема алгоритма метода правых прямоугольников
|
|
|
|
|
|
|
Изм. |
|
№ докум. |
Подп. |
Дата |
5 |
|
|
|
|
|
|
|
|
|
Перекрестная |
|
|
|
|
|
|
|
ссылка |
|
|
|
Ниже |
(таблица |
1.1) |
приведены |
результаты |
численного |
вычисления |
|
4 |
|
|
|
|
|
|
интеграла ∫ ln 2 x dx методом правых прямоугольников (при шаге разбиения 10) |
|||||||
|
1 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
и, для сравнения, – значение интеграла, вычисленного по формуле (1). |
|
||||||
Название |
Таблица 1.1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Метод |
Результат |
Сноска |
||
|
|
Ньютон-Лейбниц |
0.888065738637151 |
|
|||
|
|
Правых прямоугольников |
0.924191164970398 |
|
|||
1 Результат получен в пакете MathCAD |
|
|
|
|
|||
Изм. |
№ докум. |
Подп. |
Дата |
|
|
|
6 |
|
|
|
|
||||
|
|
|
Стиль Заголовок 1 |
|
|
Заключение |
|
|
|
|
|
|
4 |
2 x dx дает |
|
Метод правых прямоугольников для вычисления интеграла ∫ ln |
|||
|
|
|
1 |
x |
|
|
|
|
|
результат с избытком (таблица 1.1). Очевидно, что при уменьшении шага |
||||
разбиения отрезка интегрирования точность вычисления по методу возрастет. |
||||
|
|
|
Перекрестная |
|
|
|
|
ссылка |
|
Изм. |
№ докум. |
Подп. |
Дата |
7 |
|
||||
Стиль Заголовок 1
Список литературы
1.Копченова Н.В., Марон И.А. Вычислительная математика в примерах и задачах. М.: Наука, 1972. 366 с.
2.Алексеев Е.Р., Чеснокова О.В. Решение задач вычислительной математики в пакетах MathCad 12, MatLab 7, Maple 9. М.: НТ Пресс, 2006. 496 с.
Нумерованный список
|
|
|
|
|
|
|
Изм. |
|
№ докум. |
Подп. |
Дата |
8 |
|
|
|
|
