Аналитические методы расчета
Аналитическими называются методы решения, базирующиеся на аналитическом интегрировании дифференциальных уравнений, описывающих состояние нелинейной цепи с использованием аналитических выражений характеристик нелинейных элементов.
Основными аналитическими методами, используемыми при решении широкого круга задач электротехники, являются:
– метод условной линеаризации;
– метод аналитической аппроксимации;
– метод кусочно-линейной аппроксимации.
Метод условной линеаризации
Метод условной линеаризации применяется
в случаях, когда в нелинейном уравнении
одно из слагаемых в левой части мало по
сравнению с другими, вследствие чего,
без внесения существенной погрешности,
его можно соответствующим образом
линеаризовать. Благодаря этому все
уравнение становится линейным для одной
из переменных, определяющих характеристику
нелинейного
элемента, например
.
С использованием этой характеристики
находится затем временная зависимость
для
второй определяющей ее переменной по
алгоритму:
.
Метод отличается простотой, однако получаемое с его использованием решение является достаточно приближенным, вследствие чего он в основном применяется для ориентировочных расчетов.
В качестве примера использования
метода определим максимальное значение
тока в цепи на рис. 1, если
, где 
;
;
;
.
Вебер–амперная характеристика нелинейной катушки индуктивности приведена на
рис. 2.
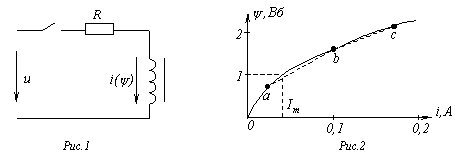
1. Запишем уравнение состояния цепи после коммутации
|
(1) |
.2. Используя метод условной линеаризации, определим второе слагаемое в левой части (1) как
|
(2) |
,
где
;
и 
- амплитуды потокосцепления и тока в установившемся послекоммутационном
режиме;
.
3. Подставив (2) в (1), получим линейное дифференциальное уравнение
,
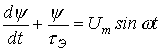решением которого на основании классического метода расчета переходных процессов является
.
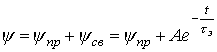4. Принужденная составляющая 
определяется соотношением
,
где 
.
Для определения
и 
предположим (с последующей проверкой), что 
. При этом условии 
и 
. По зависимости
для полученного значения
найдем
.Тогда 
и 
, т.е. сделанное выше предположение корректно.
Следует отметить, что в общем случае значения и могут быть определены, например, итерационным методом.
Определив 
, запишем
.
Поскольку по условию 
, то 
.
Таким образом,
|
(3) |
.
6. Не
решая трансцендентное уравнение, будем считать, что максимальное значение потокосцепления
имеет место примерно через полпериода своего изменения, т.е. при 
. Подставив это время в (3), получим:
По кривой 
для
найдем максимальное значение тока 
, которое в 
раз превышает амплитуду тока в установившемся послекоммутационном режиме. Напомним,
что для линейной цепи 
Примечания:
1. Обычно при использовании метода условной линеаризации для расчета переходного
процесса при подключении нелинейной катушки индуктивности к источнику синусоидального
напряжения эквивалентная линейная индуктивность 
определяется исходя из амплитудных значений тока и потокосцепления в установившемся
послекоммутационном режиме, как это и было сделано в рассмотренном выше примере.
Однако если необходимо оценить максимально возможное значение тока, то величину
индуктивности следует определять по начальному участку вебер–амперной характеристики,
где
максимальна.
2. Если сопротивление резистора в ветви с нелинейной катушкой
достаточно велико, так что 
, то следует пренебречь нелинейностью слагаемого 
, положив 
. В этом случае нелинейное уравнение (1) сводится к линейному вида
,
и соответственно кривая определяется по кривым и .