электроника / shemotech_an_i_civ_ustroystv_poln / 8. Методика синтеза комбинационных схем

8. Методика синтеза комбинационных схем

8.1. Элементы комбинационных схем. Математическим аппаратом описания комбинационных схем, отражающим логику их функционирования, является алгебра логики (булева алгебра).

В булевой алгебре переменные принимают только два значения: 0 и 1. Такие переменные называются двоичными. Над ними могут производиться три основных логических действия: сложение (операция «ИЛИ»), умножение (операция «И») и отрицание (операция «НЕ»), правила выполнения которых для двух переменных приведены в таблице 8.1.

Таблица 8.1

Аргументы		Логические операции
		ИЛИ	И	НЕ	НЕ
0 0 1 1	0 1 0 1	0 1 1 1	0 0 0 1	1 1 0 0	1 0 1 0

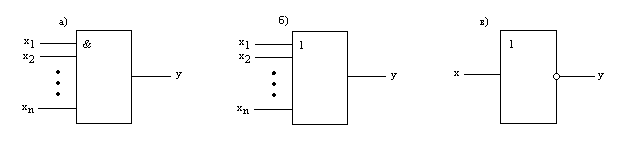
При проектировании схем на дискретных компонентах в качестве базовых элементов являлись логические схемы И, ИЛИ, НЕ на различное число входов (рис. 8.1).

И ИЛИ НЕ

Рис. 8.1. Условные обозначения логических элементов И (а); ИЛИ (б); НЕ (в)

Функциональной полнотой обладают и другие наборы логических функций. Например, - функция И-НЕ, носящая название функции Шеффера, или - функция ИЛИ-НЕ, называемая также функцией Пирса (рис. 8.2).

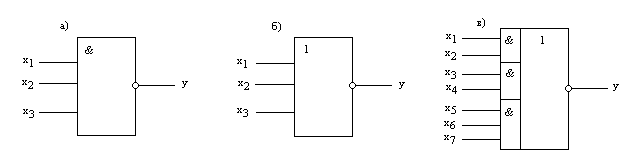
Для удобства построения сложных логических схем имеются базовые элементы, выполняющие и более сложные логические функции.

И–НЕ ИЛИ–НЕ И–ИЛИ–НЕ

Рис. 8.2. Условные обозначения логических элементов И-НЕ (а);

ИЛИ-НЕ (б); И-ИЛИ-НЕ (в)

Например, логические схемы расширенной логики реализуют функцию типа

8.2. Общие принципы синтеза комбинационных схем. Синтез логической схемы начинают с описания алгоритма ее работы исходя из функционального ее назначения. Алгоритм работы можно записать в виде таблицы истинности или логической функции, которая устанавливает функциональную взаимосвязь между входными и выходными величинами. Полученную логическую функцию требуется минимизировать. Минимизация необходима для упрощения структуры схемы.

Известно несколько способов минимизации логических функций, например, метод диаграмм Вейча.

Проиллюстрируем метод диаграмм Вейча (рисунок 8.3) на примере функции:

(8.1)

Преобразованная функция принимает один из следующих видов:

(см. рис. 8.3, а)

(см. рис. 8.3, б)

(см. рис. 8.3, в)

Рис. 8.3. Диаграммы Вейча с различными контурами

Наличие задержек в реальных логических схемах приводит к нарушению законов булевой алгебры в момент переходных процессов. Задержки порождают так называемые состязания (опасные и неопасные) сигналов, вследствие которых возможна неустойчивая работа устройств. Для устранения возможности неустойчивой работы устройств при проектировании последних необходимо либо устранить, либо скорректировать влияние опасных состязаний.

По месту возникновения состязания сигналов делят на состязания на входах устройства и состязания на входах составляющих его логических элементов.

Состязания на входах i-го логического элемента схемы возникают вследствие различных суммарных задержек распространения сигналов, поступающих на его входы. Если разница этих задержек превышает время переключения логического элемента, то на его выходе, а возможно и на выходе всего устройства, будет отрабатываться ложный сигнал.

Можно синтезировать функционально надежную схему без учета состязаний. Пусть логическая функция имеет вид:

(8.2)

Построим диаграмму Вейча так, чтобы контуры покрывали все подозрительные соседние состояния (рис. 8.4). Такой выбор контуров позволяет получить логическую функцию, при реализации которой на логических элементах, обладающих задержками переключения, будут отсутствовать статические состязания. Преобразованная таким образом логическая функция имеет вид:

(8.3)

Рис. 8.4. Синтез функционально надежной схемы: покрытие единичных (а) и нулевых (б) наборов

В логическом базисе И–НЕ ее можно записать следующим образом:

(8.4)

Для реализации этой функции требуются четыре логических элемента

И–НЕ и один инвертор.

Структурная (функциональная) схема представляет собой графическое изображение требуемых логических элементов и необходимых соединений между их входами и выходами.

Рассмотрим методику решения задачи минимизации в логических базисах И-НЕ либо ИЛИ-НЕ, широко используемых в интегральной схемотехнике. Основой для получения минимальных форм логических функций в базисах функций Пирса (ИЛИ-НЕ) либо Шеффера (И-НЕ) может служить минимальная дизъюнктивная нормальная форма, полученная в результате решения канонической задачи минимизации:

где - символ импликант, - их количество. Тогда двухкратное инвертирование функции и применение затем правила инверсии позволяют найти минимальную (по количеству букв) форму в логическом базисе И-НЕ:

Для перехода в логический базис ИЛИ-НЕ необходимо прежде осуществить двухкратное инвертирование как всей функции , так и составляющих ее импликант , , а затем воспользоваться правилом инверсии для перехода от логического произведения к логической сумме:

,

где .

Последовательность этапов синтеза комбинационных схем (КС).

1. Записать условия функционирования КС. Эти условия могут быть заданы с помощью либо таблицы истинности, либо логической функции, либо некоторой функциональной схемы. В последнем случае необходимо проверить, действительно ли эта схема имеет минимальную сложность, а также является ли она функционально надежной.

2. С использованием карты Карно определить минимальную дизъюнктивную нормальную форму (МДНФ) алгебраического выражения реализуемой функции, то есть минимизировать логическую функцию по методике синтеза функционально надежной схемы.

3. Перейти в заданный логический базис И-НЕ либо ИЛИ-НЕ (возможно, и в базис И-ИЛИ-НЕ), то есть преобразовать полученную МДНФ таким образом, чтобы при ее схемной реализации использовались бы только универсальные логические элементы.

4. Составить структурную схему в заданном элементном базисе. Каждой логической операции преобразованной логической функции ставится в соответствие определенный логический элемент заданного базиса. Связи между элементами определяются логической функцией.

8.3. Синтез комбинационных схем в заданных базисах. Положим, что функционирование комбинационной схемы описывается таблицей 8.2, которой соответствует карта Карно, представленная таблицей 8.3.

Таблица 8.2

X1	X2	X3	Y
0	0	0	1
0	0	1	0
0	1	0	0
0	1	1	0
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	1

Таблица 8.3

X3	X1X2
	00	10	11	01
0	1	0	1	0
1	0	1	1	0

С использованием карты Карно получим МДНФ в следующем виде:

Если функциональную схему необходимо реализовать на логических элементах И-НЕ, то полученная МДНФ переводится в инверсно-конъюнктивную форму путем применения операции двойной инверсии, а затем в соответствии с теоремой де Моргана, инверсия суммы переменных преобразуется в произведение инверсий переменных. В данном случае

.

Структурная схема, реализующая данную функциональную зависимость, представлена на рис. 8.5.

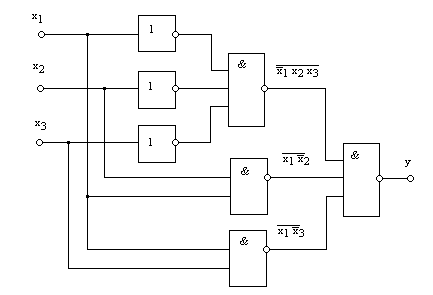
Рис. 8.5. Структурная схема на элементах И-НЕ

При реализации комбинационного узла на элементах ИЛИ-НЕ используется выражение для инверсии функции Y. МДНФ для инверсии функции представляется совокупностью клеток, заполненных нулями. Поэтому в соответствии с таблицей 8.3 получим

.

Далее, осуществляя над полученным выражением математические операции согласно вышеуказанным правилам, будем иметь

.

В результате получается логическое выражение, содержащее операции ИЛИ-НЕ. Структурная схема, реализующая данную функцию на элементах ИЛИ-НЕ, изображена на рис. 8.6.

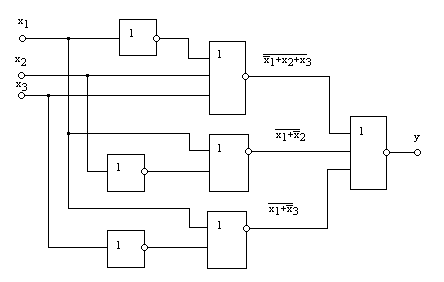
Рис. 8.6. Структурная схема на элементах ИЛИ-НЕ

8.4. Синтез схемы RS–триггера. Для синтеза изобразим таблицу истинности для RS–триггера в зависимости от комбинации входных сигналов R, S с учетом текущего состояния Qⁿ , то есть для 3-х входных величин R, S и Qⁿ (таблица 8.4).

Таблица 8.4

R	S	Qn	Qn+1
0	0	0	0
0	0	1	1
0	1	0	1
0	1	1	1
1	0	0	0
1	0	1	0
1	1	0	1/0
1	1	1	1/0

Используя таблицу истинности, запишем логическую функцию по единицам, при этом неопределенное состояние примем за единичное.

(8.5)

Изобразим карту Карно для 3-х переменных:

	1	1	1
	1	1

Рис. 8.7. Карта Карно для 3-х переменных

Сравнивая произведения логической функции (8.5) с произведениями в карте Карно, ставим единицы в тех квадратах, где содержатся такие произведения. Затем обводим контуром соседние единицы, считая соседними верхний и нижний, правый и левый квадраты. Используя законы алгебры логики (поглощения и склеивания), для каждого контура записываем упрощённые значения произведений:

(8.6)

Суммирование произведений и их упрощение позволяют записать следующее:

(8.7)

На основании полученной логической функции строим разрабатываемое устройство - в данном случае RS-триггер на элементах ИЛИ-НЕ.

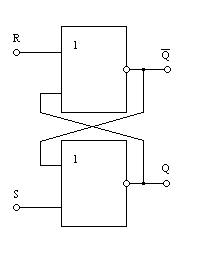
Рис. 8.8. Структурная схема RS–триггера на элементах ИЛИ-НЕ