март / Мат аппарат Часть1 / Глава1_5_прод

Радемахера не может быть базисной, так как она содержит только нечетные по отношению к середине промежутка [0, 1] функции. Для функций Уолша используют несколько способов упорядочения (нумерации). Для рассматриваемого способа обычно используют обозначение pal(p, t) и система называется упорядоченной по Пэли. Алгоритм построения системы Уолша–Пэли состоит в следующем. Сперва записывается двоичное представление номера функции

,

,

после чего pal(p, t) =. Например, pal(7, t) =, так как 7 = 2² + 2¹ + 2⁰.

Наиболее универсальным способом построения ортогональных базисных систем является использование собственных функций линейных операторов. Этот подход мы обсудим после знакомства с элементами теории линейных операторов.

Контрольные вопросы

1. Сформулируйте аксиомы скалярного произведения.

2. Запишите неравенство Коши–Буняковского и приведите пример его использования в задачах оптимизации.

3. Какие векторы называют ортогональными?

4. Как в евклидовых пространствах норму и метрику согласовывают со скалярным произведением?

5. Дайте определение гильбертова пространства Н.

6. Что такое ортогональная система векторов?

7. Докажите, что, если (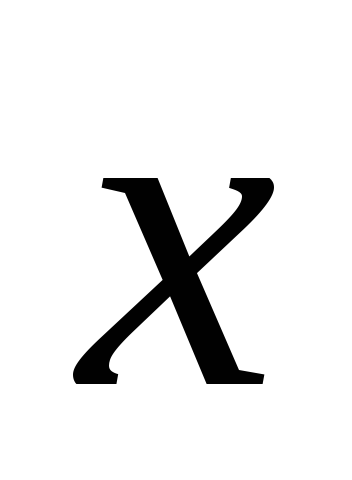, ) = 0 при любом ненулевом векторе , то = .

8. Докажите, что любая ортогональная система ненулевых векторов является линейно независимой.

9. Запишите определитель Грама для системы векторов , k = 1, 2, 3. Какой геометрический смысл он имеет?

10. Вычислите определитель Грама для системы функций , , , t > 0. Какой вывод можно сделать из полученного результата?

11. Проверьте линейную независимость векторов = (0, –1, 3), = = (1, 1, 0), = (–1, –1, 1) и с помощью процедуры Грама–Шмидта постройте ортогональную систему.

12. Дайте определение взаимного базиса.

13. Сформулируйте условия полноты и замкнутости ортонормальной системы.

14. Как вычисляются коэффициенты Фурье функции f(t) для ортонормальной системы ?

15. Сформулируйте экстремальное свойство коэффициентов Фурье для ортонормальной системы .

16. Запишите неравенство Бесселя. Дайте ему геометрическую и физическую трактовку.

17. Дайте определение классических ортогональных многочленов.

18. Постройте первые три полинома Лагерра (L₀(t), L₁(t), L₂(t)). Интервал ортогональности (0, ), весовая функция p(t) = .

19. Докажите эквивалентность систем функций , k = и .

20. Докажите ортогональность системы , на отрезке [–, ]. Превратите ее в ортонормальную систему.

21. Запишите систему функций Котельникова. Как выбираются параметры F и t базисной функции?

22. Как строится система функций Хаара?

23. Запишите представление R₁(t) и R₂(t) с помощью тригонометрической системы , .

24. Постройте функцию Уолша pal(9, t).

Глава 5. ЛИНЕЙНЫЕ ОПЕРАТОРЫ И ФУНКЦИОНАЛЫ

Оператором называют отображение элементов одного метрического пространства Х в элементы другого метрического пространства Y, что кратко записывается в форме y = Ax. Множество элементов, на котором определен оператор, называют областью определения , а соответствующее множество элементов в Y – областью значений. Если Y – числовое множество, то оператор превращается в функционал. Если X – также числовое множество, то речь идет о функции y = f(x). Если уравнение y = Ax разрешимо относительно х при любом у из области значений оператора А, т. е. х = А^–1у, то говорят, что оператор А обратим, и А^–1 – его обратный оператор.

Оператор А непрерывен, если для любой сходящейся последовательности векторов из области определения следует , где _х и _у – метрики ЛП Х и Y соответственно.

Оператор А называется ограниченным, если существует такая постоянная С, что для всякого выполняется неравенство . Наименьшее из чисел С называется нормой оператора и обозначается . Для любого ограниченного оператора А, действующего из нормированного пространства в нормированное, норму можно определить следующим образом:

=.

Понятие оператора, описывающее связь между входом и выходом системы, широко используется в современной теории систем. В информационных системах последовательное действие операторов (произведение) представляет преобразования, осуществляемые над входными данными в процессе передачи и извлечения полезной информации.

Среди операторов, действующих в линейных нормированных пространствах, наиболее общие результаты можно получить, рассматривая линейные операторы.

Определение. Пусть Х и Y – линейные нормированные пространства. Оператор А, действующий из Х в Y (), называется линейным, если выполняется принцип суперпозиции: для любых и , где – область определения оператора А, а F – поле, над которым задано ЛП Х, справедливо равенство:

.

Это означает, что линейный оператор аддитивен, , и однороден, .

Примеры линейных операторов.

1. Линейный оператор в конечномерных пространствах R_n и С_п. Рассмотрим для определенности R_n с базисом , k = 1, 2, …, n. Для произвольного вектора из R_n можно записать , и в силу линейности оператора А: . Таким образом, линейный оператор полностью определен, если известно, как он действует на базисные вектора.

Рассмотрим ЛП – область значений оператора А и выберем в нем базис , l = 1, 2, …, m, m  n. Тогда можно записать , где a_ik – координаты преобразованного базисного вектора относительно базиса , и .

Таким образом, результат действия любого линейного оператора А на вектор в конечномерном пространстве сводится к умножению вектора на матрицу оператора , i = 1, 2, …, m; k = 1, 2, …, n. Ранг этой матрицы (наивысший порядок отличных от нуля миноров) определяет размерность подпространства (область значений оператора А). Если = Х и = Y (оператор А отображает Х на Х), то базисные системы и совпадают и координаты a_ik (элементы матрицы оператора) вычисляются относительно исходного базиса .

2. Оператор поворота вектора на плоскости на угол . Ортонормальным базисом в R₂ будет система векторов = (1, 0), = (0, 1). Преобразованные (повернутые на угол ) базисные векторы можно записать в исходном базисе как и . Таким образом, матрица поворота любого вектора на плоскости имеет вид

.

Вектор = (–3, 2) после поворота на угол  будет иметь вид

А = (–3cos  – 2sin , –3sin  + 2 cos ).

3. Тождественный, или единичный, оператор Е. Он превращает любой вектор из Х в самого себя, т. е. E=. Для R_n этот оператор определяется единичной матрицей Е.

Рассмотрим наиболее употребительные линейные операторы в функциональных пространствах C [a, b] и L₂ [a, b]. Простейшим оператором в C [a, b] и L₂ [a, b] является умножение произвольной функции f(t)  C [a, b] или L₂ [a, b] на фиксированную функцию , также принадлежащую рассматриваемым ЛП, т. е. А f(t) = f(t).

Весьма важным является оператор дифференцирования. Областью его определения в С [a, b] и L₂ [a, b] является множество дифференцируемых функций. Более общим является дифференциальный оператор n-го порядка D_n, определяемый как , где _k(t) – фиксированные функции. Областью определения оператора D_n является множество n раз дифференцируемых функций.

Так, например, оператор определяет собственные колебания тока f(t) = i(t) в последовательном колебательном контуре.

Большую роль в приложениях играют интегральные операторы Фредгольма и Вольтерра . Здесь функция двух переменных K(s, t) называется ядром оператора. Обычно для С[a, b] предполагается непрерывность K(s, t) по обоим аргументам, а для L₂ [a, b] – интегрируемость квадрата ядра, т. е. . Для оператора Вольтерра обычно предполагается, что функция K(s, t) непрерывна при s < t и K(s, t) = 0 при s > t.

Сумма и произведение линейных операторов. Суммой линейных операторов А и В называют линейный оператор С, для которого . Область определения оператора С является пересечением областей определения операторов А и В.

Если операторы А и В ограничены, то .

Произведением операторов А и В называют результат их последовательного действия, т. е. . Область определения С состоит из тех , для которых , где D_B и D_A – области определения операторов В и А соответственно. Для нормы оператора С справедливо неравенство . На основании введенных определений ясно, как определять степень оператора A^k и функцию от оператора , представленную с помощью степенного ряда. По определению полагают .

Спектр оператора. Мы уже отмечали, что наличие у оператора А обратного А^–1 позволяет утверждать, что уравнение разрешимо относительно при любом . Часто вместо этого уравнения рассматривают уравнение , где  – числовой параметр. Это уравнение можно переписать в форме

, (5.1)

где Е – тождественный (единичный) оператор. Одновременно с уравнением (5.1) рассматривают уравнение

, (5.2)

которое называют однородным для уравнения (5.1). Если для данного значения  оператор А – Е имеет обратный (А – Е)^–1 = R_, называемый разрешающим оператором или резольвентой, то уравнение (5.1) имеет при любом решение, и при том только одно. Тогда однородное уравнение (5.2) при данном  имеет лишь нулевое решение. Такие значения  называются регулярными значениями оператора А. Все значения параметра , не являющиеся регулярными, образуют спектр оператора А.

Среди значений параметра , образующих спектр, могут быть такие значения ₀, ₁, …, _n, … , при которых однородное уравнение (5.2) имеет ненулевые решения . Такие значения параметра называются собственными значениями или характеристическими числами, а соответствующие им вектора – собственными векторами оператора А. Совокупность собственных значений называется дискретным (точечным) спектром оператора А.

Мы уже отмечали, что в конечномерных пространствах действие любого линейного оператора сводится к умножению вектора на матрицу оператора А = {a_ij}. Уравнение (5.1) в этом случае превратится в систему линейных уравнений вида

. (5.3)

Мы считаем в данном случае, что Х = Х ' = Y = Y ', т. е. оператор А действует из Х в Х и матрица оператора квадратная. Если определитель этой системы отличен от нуля, то есть  не является корнем уравнения D() = 0, называемого характеристическим, то записанная система уравнений имеет единственное решение при любых (правых частях) и все такие значения параметра  регулярны. Корни уравнения D() (их не более n) образуют спектр. Так как при этих значениях  однородная система, соответствующая (5.3), имеет нетривиальное решение (отличное от нуля), то любая точка спектра является собственным значением.

Таким образом, характеристические числа, или собственные значения линейного оператора в конечномерном пространстве, являются корнями характеристического уравнения D() = 0, а решения однородной системы для каждого собственного значения дают собственные векторы оператора.

Для дифференциального оператора D₂ y(t) = y''(t)+ y(t), описывающего колебательный контур без потерь, собственные значения равны а соответствующие им собственные векторы (в данном случае функции) равны exp (jt) и exp (–jt) соответственно.

Линейные функционалы и операторы в Гильбертовом пространстве. Определим на ЛП L числовую функцию , отображающую векторы из L в скаляры из поля F, над которым задано L. Выражение называется линейным функционалом, если справедлив принцип суперпозиции, состоящий в том, что для любых ,  L и , включающий в себя аддитивность и однородность .

Приведем примеры линейных функционалов.

В R_n любой линейный функционал имеет вид , где = (х₁, х₂, …, х_п) – аргумент функционала, = (а₁, а₂, …, а_п) – фиксированный вектор из R_n. Линейность данного функционала вытекает из аксиом ЛП.

В С [a, b] примером линейного функционала может служить интеграл вида , называемый в задачах обработки сигналов корреляционным интегралом, где x(t) является аргументом, а s(t) – фиксированной функцией, т. е., как уже отмечалось, скалярное произведение при фиксированном втором сомножителе по отношению к первому является линейным функционалом.

Очень важным является линейный функционал, для которого , где – функция, равная нулю всюду, кроме точки t = t₀, t  (a, b), и принимающая в t₀ бесконечно большое значение. При этом . Функция называется дельта-функцией Дирака и более подробно будет рассмотрена далее.

Рассмотрим геометрический смысл линейного функционала. Выберем для наглядности в качестве ЛП R₃ – трехмерное арифметическое пространство. Линейный функционал в R₃ задает плоскость, определяемую уравнением , где = (а₁, а₂, а₃) – фиксированный вектор. Каждому вектору соответствует точка на этой плоскости. Для произвольного ЛП линейный функционал задает гиперплоскость.

Выпуклые множества и выпуклые функционалы. Понятие выпуклости лежит в основе многих разделов теории ЛП. Оно является ключевым при решении многих задач оптимизации (выпуклое программирование)^*.

Пусть L – некоторое ЛП. Подпространство M  L называется выпуклым, если для все векторы вида , где , также принадлежат М. Геометрический смысл этого определения ясен из рис. 5.1, на котором приведены выпуклое (а) и невыпуклое (б) подпространства в R₂ (на плоскости).

Для С [a, b] множество функций, удовлетворяющих условию | f(t)|  1, выпукло, так как если | f(t)|  1 и | g(t)|  1, то

.

Для произвольного множества A  L существует наименьшее выпуклое множество, которое содержит А. Оно называется выпуклой оболочкой множества А. На рис. 5.2 штрихами показана оболочка множества А.

Важным примером выпуклой оболочки является п-мерный симплекс, который определяется следующим образом. Симплекс с вершинами ₁, ₂, …, _{п + 1} есть совокупность всех точек, представимых в виде

.

При этом векторы должны быть линейно независимы. В R_n нуль-мерный симплекс – это точка, одномерный – отрезок, двумерный – треугольник, трехмерный – тетраэдр.

С понятием выпуклости множества тесно связано понятие выпуклого функционала.

Определение. Неотрицательный функционал p()  0 для   L называется выпуклым, если выполняются следующие условия:

1. для  ,  L;

2. p() = p() для всех  > 0.

Примером выпуклого функционала может служить норма, так как сформулированные условия включаются в систему аксиом, определяющих норму.

Напомним, что гильбертовым называется бесконечномерное полное евклидово пространство H. В зависимости от того, над каким полем построено исходное ЛП (R или С), различают вещественное и комплексное H-пространства.

Для линейных функционалов в Н ключевой является теорема, утверждающая, что любой линейный функционал в Н имеет вид , где вектор однозначно определяет функционал . При этом .

Для линейных функционалов . Опираясь на неравенство Коши–Буняковского и сформулированную выше теорему, можно доказать предыдущее утверждение.

Пусть А – линейный оператор в гильбертовом пространстве Н. Рассмотрим функционал , где – фиксированный вектор из Н. Очевидно, что – линейный функционал и в соответствии со сформулированной выше теоремой . Выражая через с помощью оператора А^* получим окончательно . Оператор А^* называется сопряженным к А. Его норма равна норме исходного оператора, т. е. .

Понятие сопряженного оператора может быть введено в любом евклидовом пространстве. Так в R_n, где любой линейный оператор определяется матрицей А, сопряженным будет оператор, задаваемый сопряженной матрицей А^*. Напомним, что элементы сопряженной матрицы равны элементам a_ji исходной матрицы. В вещественном гильбертовом пространстве L₂[a, b] для интегрального оператора Фредгольма сопряженным будет оператор .