
схема все материалы / Лекционные материалы 2012 / 40 Простейшие частотно-селектирующие цепи на ОУ
.pdf
Простейшие частотно-селектирующие цепи на ОУ
В общем случае операционный усилитель в инвертирующем включении охвачен частотно-зависимой обратной связью, реализуемой 2-полюсниками
Z1( jω) и ZF ( jω) (рис. 1).
Рис. 1
Тогда комплексный коэффициент передачи зависит от частоты по зако-
ну
KF ( jω) = − ZF(( jω)) .
Z1 jω
Рассмотрим случаи, когда частотная зависимость 2-полюсников Z1( jω) и ZF ( jω) реализуется простейшими цепями, содержащими емкость.
Пусть ZF ( jω) представляет собой параллельное соединение резистора и конденсатора (рис. 2).
Рис. 2
В этом случае импеданс 2-полюсника в цепи обратной связи выражается
соотношением
1

|
RF |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ZF ( jω) = |
jωC |
|
|
|
|
|
|
R |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
= |
|
|
|
|
F |
|
, |
|
|
|
|
|||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
RF + |
|
|
|
|
1 |
+ jωCRF |
|
|
|
|
||||||||||
|
|
jωC |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
а коэффициент передачи |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
KF ( jω) = - RF |
|
|
|
|
1 |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
R1 1+ jωCRF |
|
|
|
|
|
|
||||||||||||||
Модуль коэффициента передачи K |
F |
(ω) = - |
RF |
|
|
1 |
|
, τ |
F |
= R C |
|||||||||||
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
R1 |
1+ (ωτF )2 |
|
|
F |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
– постоянная времени.
Вводя понятие частоты среза fср = 2πτ1 F и пользуясь соотношением ω = 2πf , получаем
KF ( f ) = - RF |
|
|
|
1 |
|
|
= - |
|
KF (0) |
|
|
. |
||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
ö2 |
|
|
|
|
ö2 |
||||||
R1 |
æ |
f |
|
|
æ |
f |
|
|
|
|||||
1 |
+ ç |
f |
÷ |
|
|
1+ ç |
f |
|
÷ |
|
|
|||
|
|
|
è |
|
ср ø |
|
|
è |
|
ср ø |
||||
Эта зависимость качественно изображена на рис. 3а, а соответствующая ей переходная характеристика, как реакция схемы на единичный скачок на- пряжения – на рис. 3б.
Рис. 3
Амплитудно-частотные характеристики в теории цепей и систем авто-
матического регулирования часто строятся в логарифмическом масштабе и называются логарифмическими АЧХ (ЛАЧХ). По горизонтали откладывается логарифм частоты, а по вертикали – модуль коэффициента передачи в деци- белах (рис. 4).
2
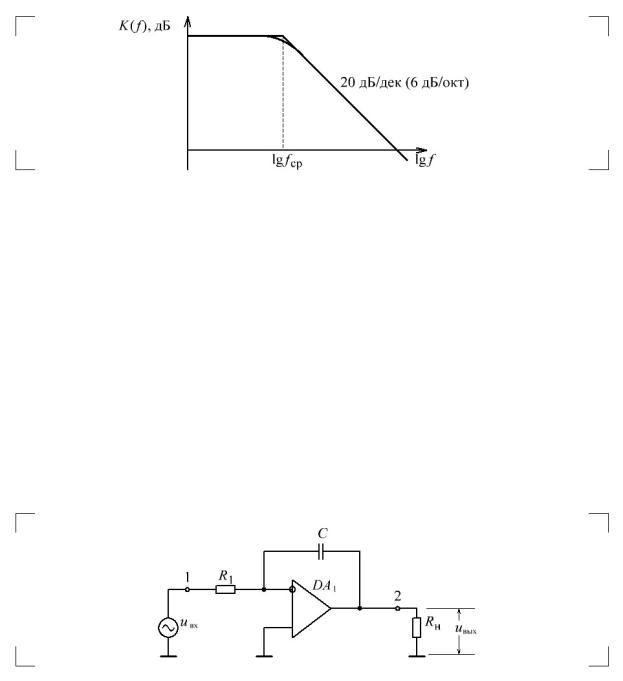
Рис. 4
В этом случае для рассматриваемой цепи график состоит из 2 прямых асимптот, пересекающихся в области lg fср . В этой области происходит
плавный переход с одной прямой на другую. Прямая ниже lg fср расположе-
на горизонтально, а выше lg fср – имеет наклон 20 дБ/декада или 6 дБ/октава.
Декада соответствует десятикратному изменению частоты, октава – двукрат- ному.
Как видно, схема представляет собой фильтр нижних частот с верхней граничной частотой, равной частоте среза.
Для этой схемы интересен частный случай, когда сопротивление в цепи обратной связи отсутствует RF → ∞ (рис. 5).
|
|
|
|
|
|
Рис. 5 |
|
|
|
|
|||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||
Тогда ZF ( jω) = |
1 |
|
, а KF ( jω) = − |
|
jωC |
|
= − |
1 |
. Модуль коэффици- |
||||||
jωC |
|
|
|
|
jωR1C |
||||||||||
|
|
|
|
|
|
|
R1 |
|
|
|
|||||
ента передачи KF (ω) = − |
1 |
= − |
1 |
. В результате KF ( f ) = − |
fср |
|
|||||||||
ωR1C |
ωτ1 |
f |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||
ЛАЧХ такой цепи имеет только одну асимптоту (рис. 6а), а переходная
характеристика во временной области выполняет интегрирование входного
3

|
1 |
t |
|
скачка напряжения uвых (t) = − |
ò2 uвх (t)dt (рис. 6б). Поэтому такая схема |
||
R C |
|||
1 |
t |
||
|
|
1 |
|
называется интегратором. |
|
||
|
|
|
|
|
|
|
|
|
Рис. 6 |
|
|
|
Включая несколько входных сигналов по схеме сумматора (рис. 7), |
||||||||||
можно |
|
|
получить |
взвешенное |
интегрирование |
сигналов |
|||||
u |
вых ( |
t |
) |
= − |
N |
1 |
t2 u |
вхi ( |
t dt . |
|
|
å R C |
|
|
|||||||||
|
|
|
ò |
) |
|
|
|||||
|
|
|
|
|
i=1 |
i |
t |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
Рис. 7
В другом случае конденсатор устанавливается последовательно с рези- стором R1 (рис. 8).
Рис. 8
Коэффициент передачи такой цепи выражается соотношением
4

|
|
KF ( jω) = - |
ZF |
( jω) |
|
= - |
|
RF |
|
|
|
= - |
RF |
|
|
|
|
|
1 |
|
|
. |
|
|
|
|
||||||||||||||
|
|
|
Z1( jω) |
|
|
|
|
|
R1 1+ |
|
|
|
|
1 |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
R + |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
jωC |
|
|
|
|
|
|
|
|
jωR1C |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Модуль |
коэффициента |
|
усиления |
|
|
|
KF |
(ω) = - |
RF |
|
|
|
|
1 |
|
|
, где |
||||||||||||||||||||||
|
|
|
|
R1 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
1+ |
|
1 |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
ωτ |
)2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
τ |
= R C . Или K |
F |
( f ) = - |
RF |
|
|
|
|
|
|
1 |
|
|
|
|
|
, где |
f |
ср |
= |
1 |
|
|
|
– частота среза. |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
1 |
1 |
|
|
|
R1 |
|
|
|
1+ |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
2πτ1 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ fср |
ö2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
f |
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Качественно эта зависимость приведена на рис. 9а, а временная реакция на скачок входного напряжения – на рис. 9б.
Рис. 9 ЛАЧХ, соответствующая данной частотной зависимости приведена на
рис. 10.
Рис. 10.
Наклоны асимптот также, как и в случае фильтра нижних частот, со- ставляют 0 и 20 дБ на декаду или 6 дБ на октаву изменения частоты.
5

Как видно, данная схема представляет собой фильтр верхних частот с нижней граничной частотой, равной частоте среза.
Если в данной схеме R = 0, то Z = |
1 |
и K |
F |
( jω) = − |
RF |
= − jωR C |
||
jωC |
1 |
|||||||
1 |
1 |
|
|
F |
||||
jωC
(рис. 11).
Рис. 11
Модуль коэффициента усиления K |
F |
(ω) = −ωR C и K |
F |
( f ) = − |
f |
, где |
||||
|
||||||||||
|
|
|
|
|
F |
|
fср |
|
||
|
|
|
|
|
|
|
|
|
|
|
fср = |
1 |
= |
1 |
. |
|
|
|
|
|
|
2πτF |
2πRFC |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
ЛАЧХ такой схемы и временная зависимость выходного напряжения, как реакция на скачок имеют вид, приведенный на рис. 12.
Рис. 12
Временная зависимость выходного напряжения имеет вид
uвых (t) = −R1C duвх (t) . dt
Поэтому схема называется дифференциатором. Если подключить не- сколько источников по схеме сумматора напряжений, то можно организовать суммирующий дифференциатор (рис. 13).
6

|
|
|
Рис. 13 |
Выходное |
напряжение этой схемы определяется формулой |
||
N |
|
duвхi (t) |
|
uвых (t) = −å R1Ci |
|
. |
|
|
dt |
||
i=1 |
|
|
|
|
|
|
|
Как видно, глубокая обратная связь совместно с большим собственным
коэффициентом усиления операционного усилителя позволяет получить свойства, не достижимые пассивными RC-цепями.
Практические аспекты применения интеграторов и дифференциаторов имеют ряд особенностей. В частности интегрирование постоянного напряже- ния дает нарастающее выходное напряжение, которое рано или поздно дос- тигнет напряжения питания и выходной каскад войдет в режим ограничения. Потребуется принудительный разряд конденсатора обратной связи.
Возрастание коэффициента передачи дифференциатора с повышением частоты входит в противоречие с уменьшением собственного коэффициента усиления операционного усилителя с частотой, что необходимо учитывать при расчете схемы.
7
