8.7. Логика с непосредственными связями

Для упрощения логической схемы с многими входами тран­зисторы иногда включают непосредственным образом (рис. 8.7, а). Такую логику называют непосредственно-связанной диодно-транзисторной логики (ДТЛ).

Обратите внимание на параллельное включение транзисто­ров. Схема с такой параллельной конфигурацией выполняет функцию ИЛИ-НЕ (рис. 8.7,6). Сигнал на входе одной или не­скольких баз транзисторов левой группы отпирает соответствую­щие транзисторы, поскольку импульс положительной полярности создает прямое смещение n — р — n-транзистора. Когда один (или несколько) из этих транзисторов отпирается и входит в насыщенное состояние, на выходе образуется практически ко­роткое замыкание вследствие очень малого полного сопротив­ления насыщенного транзистора. В этом случае падение напря­жения на резисторе R₁ равно напряжению источника, а коллек­торы оказываются под потенциалом земли. Поэтому к базам последующих транзисторов двух раздельных схем ИЛИ при­кладывается нулевое напряжение, вследствие чего эти транзи­сторы не отпираются. При отсутствии положительных сигналов на базах всех остальных транзисторов эти транзисторы оказы­ваются запертыми. В этом случае падения напряжений на ре­зисторах R₂ и Rз практически равны нулю и напряжения сигна­лов на выходах 1 и 2 равны напряжениям источников питания, причем их полярность совпадает с полярностью входного сиг­нала. Это объясняется инвертированием сигналов схемами ИЛИ, поскольку здесь используются транзисторы, включенные по схеме с общим эмиттером. Поэтому, как показано на рис. 8.7,6, выходной импульс первой схемы ИЛИ имеет отри­цательную полярность (точнее, его величина почти равна ну­лю). Когда этот сигнал поступает на входы последующих схем ИЛИ, он вновь инвертируется, так что полярность и форма сигналов на выходе соответствуют полярности и форме исход­ного сигнала.

Рис. 8.7. Логическая схема с непосредственными связями.

Если хотя бы на один из других входов схем ИЛИ, располо­женных справа на рисунке, подать сигналы положительной по­лярности, то на выходах этих схем сигналы будут иметь обрат­ную полярность (точнее, выходные сигналы будут практически равны нулю), поскольку они повторно не инвертируются.

6.8. Схема исключающее или

Для вентилей И, И-НЕ и др. удобно использовать символы, поскольку они позволяют более наглядно представлять входные и выходные логические сигналы и рабочие характеристики та­ких вентилей. Поэтому, хотя и известны различные способы реализации схемы ИЛИ (на диодах, резисторах и диодах, на транзисторах), для их обозначения используется один символ.

Иногда используемую комбинацию логических схем можно представить одним символом, определяющим все свойства ком­бинированной сложной схемы, что делает ненужным изображе­ние четырех, пяти или даже большего числа символических обо­значений отдельных схем, применяемых для реализации неко­торой операции. Примером может служить полусумматор, схе­ма которого показана на рис. 8.8. По существу полусумматор состоит из схемы ИЛИ и двух схем И, одна из которых имеет инвертированный вход. Последняя схема является схемой ИС­КЛЮЧАЮЩЕЕ ИЛИ-НЕ (ЗАПРЕТ). Эти три логические схе­мы связаны между собой, как показано на рис. 8.8, а, хотя для индикации комбинации схем И и ИСКЛЮЧАЮЩЕЕ ИЛИ-НЕ, но без выхода для цифры переноса часто используют один сим­вол, изображенный на рис. 8.8, б. Этот символ соответствует схеме ИСКЛЮЧАЮЩЕЕ ИЛИ [Эта логическая схема известна под названием схемы неравнозначности или двухвходовой суммы суммирования по модулю 2. — Прим. ред.]. Если после схемы, показан­ной на рис. 8.8,6, следует инвертор (рис. 8.8, в), то получаем схему ИСКЛЮЧАЮЩЕЕ ИЛИ-НЕ (схема эквивалентности или равнозначности), символ которой изображен на рис.8.8,г.

Полные сумматоры (последовательного типа) могут быть получены путем использования двух полусумматоров, показан­ных на рис. 8.8, а. Полусумматоры применяются также для це­лей переключений и для преобразования кодов.

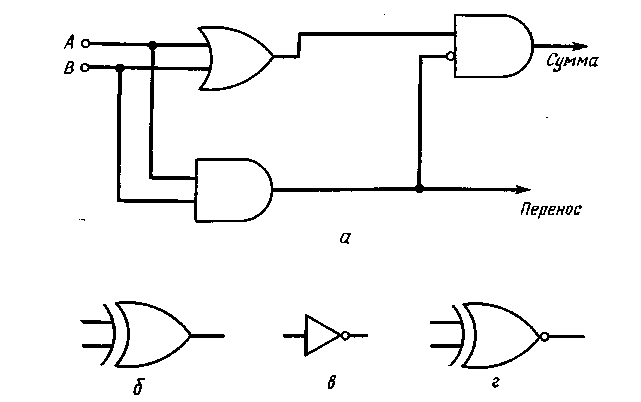
Рис. 8.8. Полусумматор (а) и условные обозначения схем ИСКЛЮЧАЮЩЕЕ ИЛИ (б), НЕ (в) и ИСКЛЮЧАЮЩЕЕ ИЛИ-НЕ (г).

Если на .входы схемы ИЛИ поступают два импульса, то они одновременно появятся и на схеме И. Тогда на выходе этой схемы И возникает импульс, который поступает на вход схемы ЗАПРЕТ и закрывает эту схему, препятствуя вводу сигналов от схемы ИЛИ. Следовательно, логика работы данной схемы такова: когда на обоих входах схемы ИЛИ действуют 1, то на выходе «Сумма» появляется 0, а на выходе «Перенос» — 1.

Таблица 8.5

А	в	Сумма	Перенос
0	0	0	0
1	0	1	0
0	1	1	0
1	1	0	1

При подаче импульса только на один какой-нибудь вход схемы ИЛИ импульс запрета не формируется. В этом случае импульс, соответствующий 1, образуется только на выходе «Сумма». Выполняемая логическая операция соответствует правилу двоичного сложения 1 + 1 = 10 (двоичное число два). Поэтому, если на входах А и В действуют единичные сигналы, то выходной сигнал на выходе «Сумма» соответствует 0 (им­пульс отсутствует), но возникает импульс переноса на выходе «Перенос» представляемый 1 старшего разряда в двоичном числе 10.

Рис. 8.9. Преобразователь кода Грея в двоичный код.

На основе описания данной логической схемы может быть составлена таблица истинности (табл. 8.5), иллюстрирующая операции, выполняемые схемой (полусумматором).

Комбинацию схем ИСКЛЮЧАЮЩЕЕ ИЛИ можно исполь­зовать для преобразования кода Грея в двоичный код (рис. 8.9). Код Грея называют также циклическим кодом или кодом с ми­нимальными ошибками. Код Грея широко применяется в вы­числительных и управляющих системах, поскольку при этом уменьшаются случайные ошибки в дроцессе работы. Это объ­ясняется тем, что по мере возрастания чисел в коде Грея в не­который момент времени изменяется только одна цифра. В дво­ичном коде это не так (табл. 8.6).

В преобразователе, показанном на рис. 8.9, количество логи­ческих схем ИСКЛЮЧАЮЩЕЕ ИЛИ равно количеству разря­дов преобразуемых чисел. Предположим, что слева в схему вво­дится число в коде Грея 1010 (01010). [Заметим, что на выхо­дах схем сигнала переноса не образуется (1 + 1=0).] Нуль, цо-ступающий на верхний вход схемы А, передается и на выход, поскольку вход непосредственно соединен с выходом. При по­даче 1 на нижний вход схемы А на выходе этой схемы также формируется 1. Но выход этой схемы связан с входом схе­мы В. Поскольку на нижний вход схемы В сигнал не поступа­ет (подается сигнал, соответствующий нулю), на выходе фор­мируется 1. Эта 1 подается на верхний вход схемы С и так как на нижний вход этой схемы также поступает 1, то на ее выхо­де получаем 0. Аналогично этому, поскольку на входы схемы D сигналы не поступают (подаются нули) , то на выходе также получается 0. Таким образом, число 1010 в коде Грея преобра­зуется в двоичное число 1100 (табл. 8.6).

Таблица 8.6

Десятичное число	Двоичный код	Код Грея
0	0000	0000
1	0001	0001
2	0010	0011
3	0011	0010
4	0100	0110
5	0101	0111
6	0110	0101
7	0111	0100
8	1000	1100
9	1001	1101
10	1010	1111
11	1011	1110
12	1100	1010

Рис. 8.10. Схема считывания двоичного числа в прямом и обратном кодах.