Типовой расчет Кибернетика (ИИИ) 4 вар
.doc
Московский государственный технический университет радиотехники, электроники и автоматики
МАТЕМАТИЧЕСКИЙ АНАЛИЗ
III семестр
Контрольные задания для студентов факультета Кибернетики
Контрольные задания по теме: «РЯДЫ»
https://www.zachet.ru/reshebnik-kontrolnogo-zadaniya-po-matematicheskomu-analizu-iii-semestr-kibernetika-mgtu-mirea/
Наша группа вКонтакте
https://vk.com/zachet_ru
URL в Google+
https://plus.google.com/+ZachetRu_channel
https://twitter.com/zachet_ru
С Уважением,
https://www.zachet.ru/
Московский государственный технический университет радиотехники, электроники и автоматики
МАТЕМАТИЧЕСКИЙ АНАЛИЗ
III семестр
Контрольные задания для студентов факультета Кибернетики
Контрольные задания по теме: «РЯДЫ»
Вариант 4
Задача 1. Исследовать на сходимость числовые ряды:
а)
; б)
.
Решение.
а) Это знакочередующийся ряд. По признаку
Лейбница, он сходится, если абсолютные
величины его членов монотонно убывают,
а общий член стремится к нулю. Первое
условие выполняется, так как
.
Второе условие тоже выполняется, т.к.
.
Значит, ряд
сходится.
б) Для этого ряда необходимое условие
сходимости не выполняется:
,
значит, ряд
расходится.
Задача 2. Исследовать знакочередующийся
ряд
на абсолютную и условную сходимость.
Решение.
Рассмотрим ряд, состоящий из абсолютных
величин данного ряда
.
Для этого ряда необходимое условие
сходимости выполняется:
.
Известно, что ряд
–
расходится. Так как
,
,
то по второму признаку сравнения рядов,
ряд
расходится.
Рассмотрим знакочередующийся ряд
.
По признаку Лейбница, он сходится, если
абсолютные величины его членов монотонно
убывают, а общий член стремится к нулю.
Первое условие выполняется, так как
.
Второе условие тоже выполняется, т.к.
.
Значит, ряд
сходится.
Таким образом, ряд является условно сходящимся.
Задача 3. Найти интервал сходимости
степенного ряда. Исследовать поведение
ряда на концах интервала сходимости.
.
Решение.
По признаку Даламбера получим
,
т.е. радиус сходимости
.
Интервал сходимости найдем из неравенства
.
Отсюда,
.
При
получим:
.
Для этого ряда необходимое условие
сходимости не выполняется:
,
значит, ряд
расходится.
При
получим:
.
Это знакопеременный ряд. По признаку
Лейбница, он сходится, если абсолютные
величины его членов монотонно убывают,
а общий член стремится к нулю. Второе
условие не выполняется, т.к.
.
Значит, ряд
расходится.
Таким образом, ряд сходится при .
Задача 4. Разложить функцию
в ряд Тейлора по степеням
.
Указать область сходимости полученного
ряда. Найти
.
а)
,
; б)
,
.
Решение.
а)
.
.
,
.
,
.
,
.
,
.
…
,
.
Таким образом,
.
.
б) .
.
,
.
,
.
,
.
,
.
…
.
Таким образом,
.
.
Задача 5. Используя признак Вейерштрасса, доказать равномерную сходимость функционального ряда на указанном промежутке.
,
.
Решение.
Рассмотрим ряд
,
причем
при
.
Так как ряд
сходится, то данный функциональный ряд
сходится равномерно и абсолютно.
Задача 6.
а) Разложить функцию
,
заданную на полупериоде
,
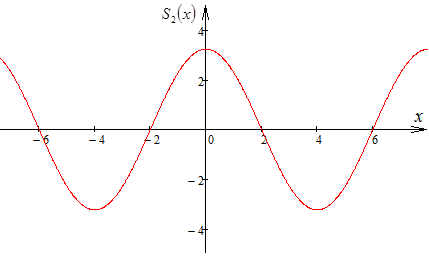
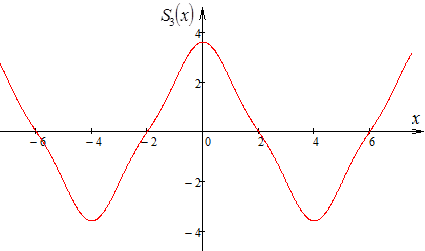
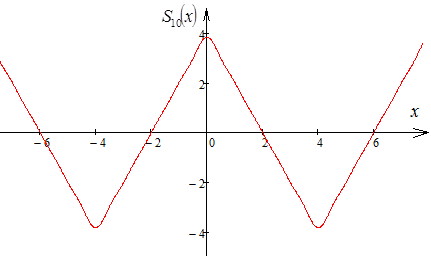
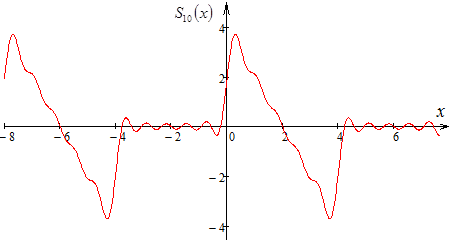
в ряд Фурье по косинусам. построить
график второй, третьей, десятой частичных
сумм. Написать равенство Парсеваля для
полученного ряда. Сумму какого числового
ряда можно отыскать с помощью полученного
равенства?
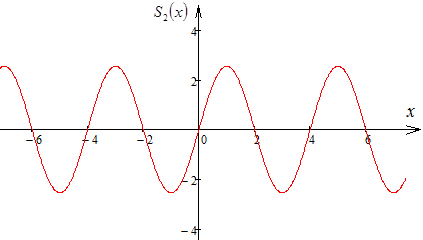
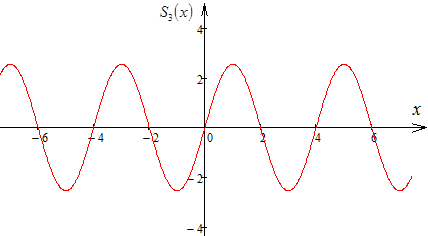
б) Разложить функцию , заданную на полупериоде , в ряд Фурье по синусам. Построить графики второй, третьей, десятой частичных сумм. Указать тип сходимости полученного ряда.
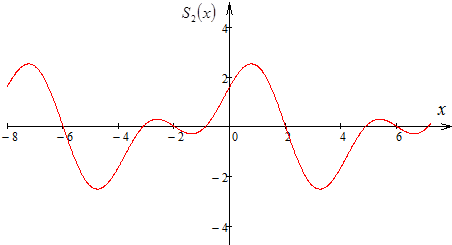
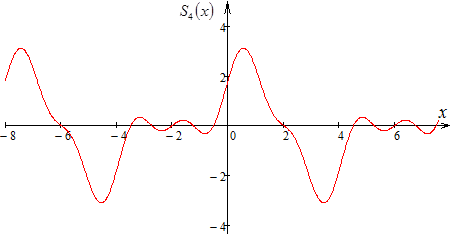
в) Разложить функцию
в ряд Фурье, продолжая ее на полупериод
функцией, равной 0. Построить графики
второй, четвертой, десятой частичных
сумм. Указать тип сходимости полученного
ряда.
,
.
Решение.
а) Ряд Фурье по косинусам имеет вид
,
где
.
Найдем эти коэффициенты:
.
.
Получаем,
.
Равенство Парсеваля:
.
б) Ряд Фурье по синусам имеет вид
,
.
Найдем эти коэффициенты:
.
Получаем,
.
в) Ряд Фурье имеет вид
,
,
.
Найдем эти коэффициенты:
;
;
.
Получаем,
.
Задача 7. Методом Фурье найти решение
уравнения колебаний струны
длины
,
закрепленной на концах:
и удовлетворяющей следующим начальным
условиям:
,
.
;
,
.
Решение.
По методу Фурье уравнение
имеет следующее решение:
.
Постоянные
и
можно найти, используя краевые условия:
,
;
,
,
,
где
.
При найденных значениях
получаем
,
или
,
т.к. каждому значению
отвечают свои постоянные
и
,
а постоянную
включаем в
и
.
Таким образом,
.
Решение должно удовлетворять начальным условиям:
,
.
,
,
.
,
откуда
.
Таким образом,
.
Задача 8. Найти приближенное решение
задачи Коши
,
,
.
Решение задачи Коши ищется в виде
степенного ряда
,
коэффициенты которого вычисляются
последовательно. Ограничиваясь суммой
,
содержащей
член ряда, получаем приближенное решение.
Оценка погрешности этого решения в
работе облегчается тем, что получающиеся
степенные ряды – знакочередующиеся.
Требуется, чтобы эта погрешность не
превосходила
при
.
,
.
Решение.
Будем искать решение этого уравнения
в виде ряда
.
Тогда
,
.
Подставляя
,
и
в исходное уравнение, получим
.
Сгруппируем члены с одинаковыми степенями
:
.
Приравнивая коэффициенты при
,
а также приравнивая нулю все остальные
коэффициенты полученного ряда, находим:
,
,
,
… ,
,
где
.
Последнее соотношение позволяет найти
последовательно все коэффициенты
искомого разложения.
Т.к.
,
то
,
т.е.
.
Т.к.
,
то
,
т.е.
.
Найдем коэффициенты:
,
,
,
,
.
Тогда
.
.
При
член ряда равен
;
—
.
Таким образом, с погрешностью
.
Задача 9. Приближенно вычислить
определенный интеграл. Для вычисления
интеграла функцию
разлагают на отрезке интегрирования в
степенной ряд, который интегрируют
почленно. Ограничившись несколькими
первыми слагаемыми полученного таким
образом числового ряда, имеем приближенное
значение интеграла. В работе погрешность
приближения не должна превышать
,
и оценка этой погрешности упрощается
по тем же причинам, что и в задаче 8.
.
Решение.
Т.к. разложение
в ряд имеет вид
,
то получим
.
Найдем такой член ряда, модуль которого не превосходит :
:
,
:
,
:
,
:
,
:
, 
:
.
Тогда
.
Задача 10. а) Найти преобразование
Фурье (спектральную плотность
)
следующей функции (сигнала)
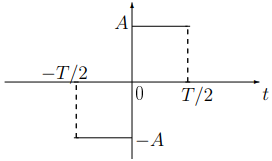
б) Продолжить периодическую функцию
(сигнал) с интервала
на всю числовую прямую, разложить в ряд
Фурье. Построить графики второй и третьей
частичных сумм.
Решение.
а)
.
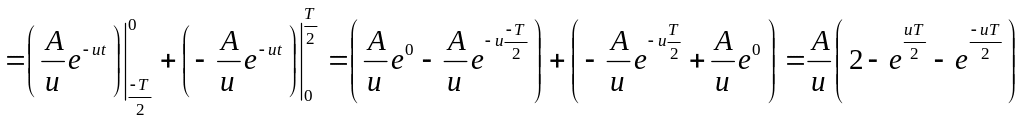б) Ряд Фурье имеет вид , где , .
Найдем эти коэффициенты:
;
;
.
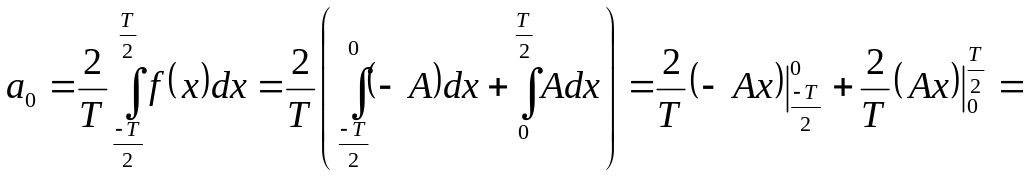
Получаем,
.
,
.
