otchet_po_laboratornoy_rabote_1
.docx
 ПЕРВОЕ
ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ
РОССИИ
ПЕРВОЕ
ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ
РОССИИ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«Санкт-Петербургский Горный университет»
Кафедра общей и технической физики
ОТЧЁТ
По лабораторной работе №1
«Оценка точности прямых и косвенных измерений»
Выполнил студент группы ПЭ-18-2 Смирнов В.А,
Проверил: Преподаватель Скалецкая И.Е.
Санкт-Петербург
2018
Содержание отчета
Цель работы: обработать данные прямых и косвенных измерений физических величин.
Возникновение погрешностей в ходе измерений: при измерении физических величин с помощью даже самых точных и совершенных средств и методов их результат всегда отличается от истинного значения измеряемой физической величины, т.е. определяется с некоторой погрешностью.
Погрешность средств измерения - это разность между результатом измерения величины и настоящим (действительным) значением этой величины. Для рабочего средства измерения настоящим (действительным) значением измеряемой величины считается показание рабочего эталона более низкого разряда.
Причины возникновения погрешностей:
- несовершенство измерительных приборов (инструментальные погрешности),
- несовершенство выбранного метода измерений или влияния лабораторных приборов на измеряемую величину (методологические погрешности),
- влияние внешних условий на одну или несколько величин, влияющих на результат, например, температуры, влажности воздуха, внешних электрических и магнитных полей и т.п. (внешние погрешности),
- неправильный отсчет показаний приборов, невнимательность и небрежность исследователя (субъективные погрешности).
Прямое измерение - измерение, проводимое прямым методом, при котором искомое значение физической величины получают путем сравнения этой величины с ее единицей.
Косвенное измерение - вычисление измеряемой величины по некоторой расчетной формуле, куда входят константы и результаты прямых измерений.
Класс точности - основная метрологическая характеристика прибора, определяющая допустимые значения основных и дополнительных погрешностей, влияющих на точность измерения.
Закон Ома для участка цепи: сила тока I, текущего по металлическому проводнику (при отсутствии сторонних сил), пропорциональна падению напряжения U на проводнике:
I = U/R,
где I - сила тока в цепи, [I] = A (Ампер); U - напряжение в цепи, [U] = В (вольт); R - сопротивление проводника, [R] = Ом.
R = рl/S,
Где - p удельное сопротивление, [p]= Ом·м ; l - длина проводника, [l] = м (метр); S - площадь поперечного сечения, [S] = м2
Удельное сопротивление характеризует способность вещества проводить электрический ток и зависит от химической природы вещества и условий в которых находится проводник.
p = RS/l
Площадь поперечного сечения S рассчитывается по измеренному значению диаметра d:
S = πd2/4
Сопротивление R вычисляется по измеренным значениям напряжения U и тока I в цепи согласно закону Ома:
R = U/I
Исходя из выше указанных формул, получается выражение для нахождения удельного сопротивления:
p = Uπd2/4Il
Величины l, d, U и I измеряются соответствующими приборами с определенной точностью. В общем случае результат любого измерения величины х представляют в виде
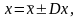
где
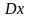 - погрешность или ошибка в измерениях
х.
- погрешность или ошибка в измерениях
х.
Измерения величины тока I и напряжения U проводят с помощью электроизмерительных приборов (амперметра и вольтметра). Точность этих приборов характеризуют приведенной погрешностью

где хпр - наибольшее значение величины, которое может быть измерено по шкале прибора.
Приведенная погрешность, измеренная в процентах, определяет класс точности прибора (указан на шкале).
Абсолютная погрешность прибора в любом месте шкалы
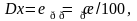
где К - класс точности прибора.
Основные расчётные формулы:


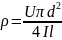
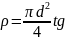
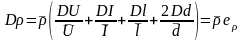
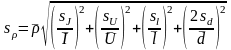
Формулы погрешности косвенных измерений:
d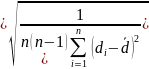
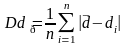
ΔR
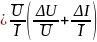
R


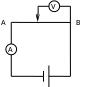 Схема
установки:
Схема
установки:
АB-исследуемый участок
Таблица 1
Прибор |
d1 |
d2 |
d3 |
d4 |
d5 |
d6 |
d7 |
d8 |
d9 |
d10 |
|
|
|
Размерность |
М 10-3 |
М 10-3 |
М 10-3 |
М 10-3 |
М 10-3 |
М 10-33 |
М 10-3 |
М 10-3 |
М 10-3 |
М 10-3 |
М 10-3 |
М 10-3 |
М 10-3 |
Штангенциркуль |
0,50 |
0,55 |
0,60 |
0,55 |
0,50 |
0,50 |
0,55 |
0,50 |
0,60 |
0,50 |
0,535 |
0,01 |
0,0055 |
Микрометр |
0,50 |
0,56 |
0,58 |
0,55 |
0,52 |
0,51 |
0,57 |
0,48 |
0,56 |
0,52 |
0,535 |
0,016 |
0,0046 |
Прибор |
|
|
Размерность |
10-2 |
10-2 |
Штангенциркуль |
0,0186 |
0,01 |
Микрометр |
0,0299 |
0,0086 |
Таблица 2:
№ опыта Размерность |
l м 10-2 |
Δl м 10-2 |
I А 10-3 |
ΔI А 10-3 |
U В
|
ΔU , B
|
R ОМ
|
ΔR ОМ 10-2 |
R ОМ 10-2 |
1 |
5 |
0,05 |
3,75 |
200 |
0,10 |
0,0225 |
0,5 |
14,2 |
11,767 |
2 |
10 |
0,05 |
3,75 |
200 |
0,15 |
0,0225 |
0,75 |
14,2 |
11,767 |
3 |
15 |
0,05 |
3,75 |
200 |
0,18 |
0,0225 |
0,9 |
14,2 |
11,767 |
4 |
20 |
0,05 |
3,75 |
200 |
0,23 |
0,0225 |
1,15 |
14,2 |
11,767 |
5 |
25 |
0,05 |
3,75 |
200 |
0,26 |
0,0225 |
1,3 |
14,2 |
11,767 |
6 |
30 |
0,05 |
3,75 |
200 |
0,30 |
0,0225 |
1,5 |
14,2 |
11,767 |
7 |
35 |
0,05 |
3,75 |
200 |
0,34 |
0,0225 |
1,7 |
14,2 |
11,767 |
8 |
40 |
0,05 |
3,75 |
200 |
0,40 |
0,0225 |
2 |
14,2 |
11,767 |
9 |
45 |
0,05 |
3,75 |
200 |
0,44 |
0,0225 |
2,2 |
14,2 |
11,767 |
10 |
50 |
0,05 |
3,75 |
200 |
0,47 |
0,0225 |
2,35 |
14,2 |
11,767 |
Пример вычислений:
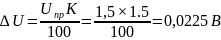
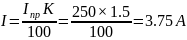
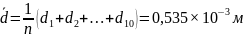
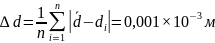
d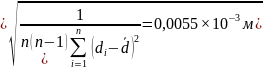
ΔR
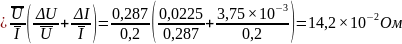
R
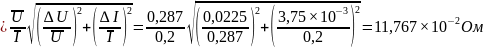
ГРАФИК
Таблица данных для графика:
l, м |
R, Ом |
0,05 |
0,5 |
0,1 |
0,75 |
0,15 |
0,9 |
0,2 |
1,15 |
0,25 |
1,3 |
0,3 |
1,5 |
0,35 |
1,7 |
0,4 |
2 |
0,45 |
2,2 |
0,5 |
2,35 |
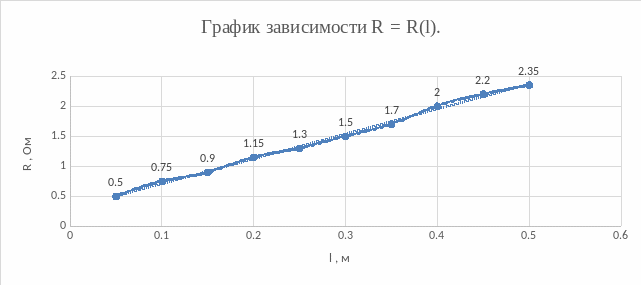
Расчёты:
1)
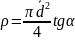 где
где


2)
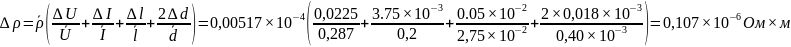
3)
=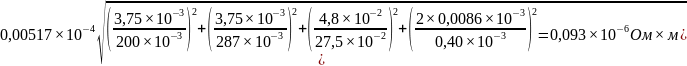
Вывод:
В данной лабораторной работе мною были произведены измерения и вычисления для определения удельного сопротивления предложенного проводника. В процессе измерений мною были использованы два прибора: штангенциркуль и микрометр, но для уменьшения погрешности, при вычислении были использованы значения микрометра. Результаты получились следующие:
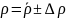
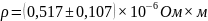
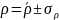
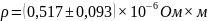
Полученная погрешность имеет небольшое значение, что даёт право говорить об отсутствии грубых ошибок при измерениях и вычислениях. Следуя из всего вышесказанного можно сделать вывод, что данный метод вычисления, при данных приборах можно использовать для определения удельного сопротивления.

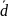
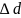
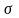 d
d