Laboratornaya_rabota_7
.docxПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ
|
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ОБРАЗОВАНИЯ
САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ
Кафедра общей и технической физики
ОТЧЕТ
По лабораторной работе № 7
По дисциплине: Физика
(наименование учебной дисциплины согласно учебному плану)
Тема: Определение момента инерции твердых тел с помощью маятника Максвелла
Выполнила: студент гр. СПС-18 ________ Гурина Э.Э.
(шифр группы) (подпись) (Ф. И. О.)
Проверил: доцент каф. ОТФ ________ Фицак В. В.
(должность) (подпись) (Ф. И. О.)
Санкт-Петербург
2019
Цель работы: изучение маятника Максвелла и определение с его помощью момента инерции твердых тел.
Краткие теоретические сведения:
а) Явление, изучаемые в работе:
Инерция твердых тел
б) Определения (основных физических понятий, объектов, процессов и величин):
Момент инерции – мера инертности тела при вращательном движении. Момент инерции тела зависит от размеров и формы тел и от распределения массы тела относительно оси вращения.
Вычисляется по формуле:

Или (в случае непрерывного распределения масс):
 ,
,
где mi - масса элемента, кг;
ri - расстояние от элемента до оси вращения, м;
-
плотность вещества в элементе объема
dV,
находящегося
на расстоянии r
от оси вращения, кг/ .
.
 Маятник
Максвелла представляет собой однородный
диск С, через центр которого проходит
металлический стержень D
(рис.1). К концам этого стержня прикреплены
две нити. Они тщательно, виток к витку,
наматываются на стержень в направлении
от его конца к диску. При освобождении
маятника возникает поступательное
движение вниз и вращательное вокруг
оси симметрии. Вращение, продолжаясь
по инерции в низшей точке движения
(когда нити уже размотаны), приводит
вновь к наматыванию нити на стержень,
диск поднимается и движение снова
повторяется, т.е. возникают колебания.
Маятник
Максвелла представляет собой однородный
диск С, через центр которого проходит
металлический стержень D
(рис.1). К концам этого стержня прикреплены
две нити. Они тщательно, виток к витку,
наматываются на стержень в направлении
от его конца к диску. При освобождении
маятника возникает поступательное
движение вниз и вращательное вокруг
оси симметрии. Вращение, продолжаясь
по инерции в низшей точке движения
(когда нити уже размотаны), приводит
вновь к наматыванию нити на стержень,
диск поднимается и движение снова
повторяется, т.е. возникают колебания.
в) Законы и соотношения (использованные при выводе расчетной формулы):
Закон сохранения энергии – полная механическая энергия в замкнутых системах отсчета есть величина постоянная.
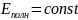
Теорема Штейнера – момент инерции тела относительно произвольной неподвижной оси равен сумме момента инерции этого тела относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями.

 – момент
инерции относительно оси, проходящей
через центр масс тела; кг*м2
– момент
инерции относительно оси, проходящей
через центр масс тела; кг*м2
m – масса тела; кг
d – расстояние между осями, м.
Схема экспериментальной установки:
 1
– основание;
1
– основание;
2 – колонка;
3 – фотоэлектронный датчик;
4 – нити;
5 – диск;
6 – ось;
7 – подвижный нижний кронштейн;
8 – основа;
9 – неподвижный верхний кронштейн;
10 – электромагнит;
11 – фотоэлектрический датчик;
12 – сменные кольца.
Основные расчетные формулы:
1. Среднее значение времени падения маятника:
 ,с
,с
n – количество измерений;
 – экспериментальное
значение времени, с.
– экспериментальное
значение времени, с.
2. Общая масса маятника:
 ,
кг
,
кг
 – масса
оси маятника, кг;
– масса
оси маятника, кг;
 – масса
диска, кг;
– масса
диска, кг;
 – масса
кольца, кг.
– масса
кольца, кг.
3. Экспериментальное значение момент инерции маятника:
 ,
кг*м2
,
кг*м2
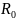 – радиус
оси маятника, м;
– радиус
оси маятника, м;
g
– ускорение свободного падения,
 ;
;
h – длина маятника, м.
4. Теоретическое значение момента инерции маятника:
 ,
кг*м2
,
кг*м2
 – момент
инерции оси маятника,
– момент
инерции оси маятника,
 ;
;
 -
момент инерции диска,
;
-
момент инерции диска,
;
 – момент
инерции кольца, надетого на диск,
– момент
инерции кольца, надетого на диск,

5. Момент инерции оси маятника:
 ,
кг*м2
,
кг*м2
 -
радиус оси маятника, м;
-
радиус оси маятника, м;
6. Момент инерции диска:
 ,
кг*м2
,
кг*м2
 -
радиус диска, м;
-
радиус диска, м;
7. Момент инерции кольца, надетого на диск:
 ,
кг*м2
,
кг*м2
Формула для расчета средней квадратичной погрешности:

 -
момент инерции маятника;
-
момент инерции маятника;
 – средняя
квадратичная погрешность массы маятника;
– средняя
квадратичная погрешность массы маятника;
m – общая масса маятника;
 -
средняя квадратичная погрешность
радиуса оси маятника;
-
средняя квадратичная погрешность
радиуса оси маятника;
- радиус оси маятника;
g – ускорение свободного падения;
t – среднее значение времени падения маятника;
 -
средняя квадратичная погрешность
среднего времени падения маятника;
-
средняя квадратичная погрешность
среднего времени падения маятника;
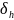 -
средняя квадратичная погрешность длины
маятника;
-
средняя квадратичная погрешность длины
маятника;
h – длина маятника.
Таблица 1. Измерение времени падения маятника по прибору.
|
t |
|
|
|
|
|
|
|
№\ед.изм |
с |
с |
кг |
кг*м2 |
кг*м2 |
кг*м2 |
кг*м2 |
кг*м2 |
1 |
2,172 2,161 2,141 2,169 2,153 2,164 2,191 2,139 2,168 2,142 |
2,159 |
0,264 |
0,161* 10-5 |
11,6* 10-5 |
122,9* 10-5 |
134,661* 10-5 |
58,665* 10-5 |
2 |
2,374 2,225 2,200 2,208 2,198 2,193 2,203 2,199 2,189 |
2,218 |
0,394 |
183,4* 10-5 |
195,161* 10-5 |
81,146* 10-5 |
||
3 |
2,278 2,291 2,339 2,250 2,254 2,234 2,257 2,222 2,243 2,210 |
2,256 |
0,523 |
243,5* 10-5 |
255,261* 10-5 |
103,693* 10-5 |
Пример вычислений:
а) Исходные данные:
 =
0,264 кг
=
0,264 кг
 =
0,394 кг
=
0,394 кг
 =
0.523 кг
=
0.523 кг
= 0,124 кг
= 0,0322 кг
h
= 41
 м
м
 =
52,95
=
52,95
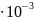 м
м
= 43,05 м
= 4,05 м
б) Погрешности прямых измерений:
 =
=
 с
с
 =
5
=
5
 м
м
 =
1
=
1
 м
м
 =
кг
=
кг
 =
кг
=
кг
 =
=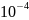 кг
кг
в) Вычисления:

 кг
кг
 58,665*10-5
58,665*10-5
 0,161*10-5
0,161*10-5

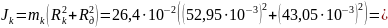 122,9*
122,9*
10-5

г) Вычисление погрешностей:
=
Графический материал
График 1. Зависимость момента инерции тела от его массы.

Результат:
=


Сравнение справочных и экспериментальных значений в процентах:
 =
58,38%
=
58,38%
 на
58,38 %
на
58,38 %
Вывод: в ходе изучения маятника Максвелла и определения с его помощью момента инерции твердых тел было установлено, что, чем больше масса тела, тем больше его момент инерции (т. е. момент инерции твердого тела прямо пропорционален его массе), а также то, что теоретическое значение момента инерции твердого тела больше экспериментального значения на 58,38 %.