12.4.3. Связь принципа максимума с уравнением Эйлера

Принцип максимума относится к числу вариационных методов и дает одинаковые с

вариационным исчислением результаты, если на экстремали не наложены никакие ограничения.

Покажем эту связь в более общей форме.

Допустим, что объект управления описывается уравнением .

Допустим, что функционал задан определенным интегралом .

Вводим дополнительную переменную , так, что.

Записываем систему уравнений: .

Составляем функцию и систему уравнений для функций:

Определим значение доставляющее максимум:

Из уравнения следует, чтоconst. Примем и подставляем в уравнение для. С другой стороны, подставляяво второе уравнение

и интегрируя, находим .

Приравнивая правые части, получаем уравнение Эйлера в интегральной форме:

.

Продифференцируем обе части полученного уравнения по времени, принимая во внимание, что ,:

Используя введенные ранее обозначения:

- получимто-есть, уравнение Эйлера.

12.4.4. Пример применения метода Понтрягина.

Определить оптимальную диаграмму тока якоря двигателя постоянного тока при отработке максимального угла поворота вала за заданное время при ограничениях на потери и тока

Решение.

Уравнения, описывающие объект управления:

Критерий оптимальности:

Les limitations :

1. Добавляем новую переменную так что . (берем в качестве добавочной переменной величину ограничения так как функционал не зависит от управления, в качестве которого принят ).

2. Составляем функцию

3. Определяем значение тока, при котором имеет место : откуда

4. Составляем уравнения для определения :

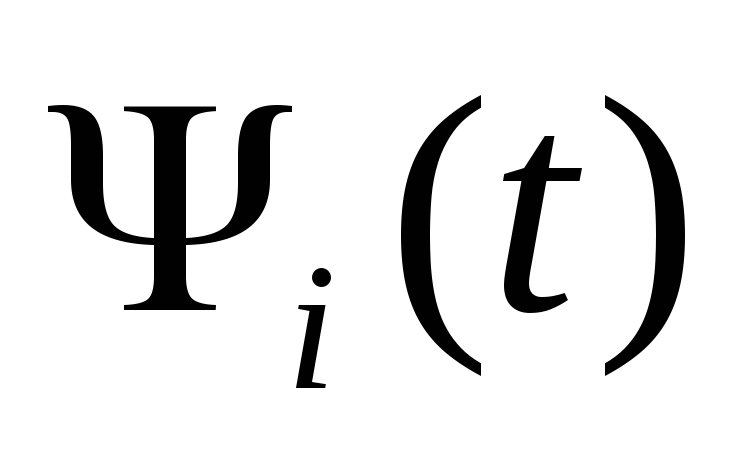5. В результате, мы имеем три уравнения : 1)

Решение этих уравнений следующее:

Согласно принципа максимума (); примем Подставляя значения в уравнение тока, получаем Это уравнение прямой, однако поэтому можно написать:

То-есть, если ток превышает значение тока ограничения, он равен этому значению. График тока показан на рис. 12.2.

Коэффициенты могут быть определены из совместного решения уравнений системы и уравнений ограничений. Используем в нашем случае уравнения тока и скорости вращения двигателя: и уравнение ограничения. Используя значения начальных условий, получаем:

d’où .

Интегрируя имеем

Откуда И для имеем:

Окончательно, уравнение тока:

Уравнение скорости вращения

12.5. Динамическое программирование - метод решения задач оптимального управления

12.5.1 Общие сведения

Метод динамического программирования был предложен американским ученым Беллманом почти одновременно с публикацией принципа максимума. Более полное изложение метода было дано в книге Р. Беллмана «Динамическое программирование», вышедшей в свет в 1960 году.

Метод динамического программирования (МДП) предназначался для решения широкого класса задач оптимального управления. Этот метод применим также к обширной сфере технических и экономических проблем.

При обосновании метода МДП предполагается, что функционал, выражающий критерий оптимальности, является дифференцируемой функцией переменных состояния. В ряде случаев, решаемых МДП, это условие не выполнялось, что дало основание утверждать, что МДП скорее хороший эвристический прием, чем математическое решение задачи.

После того, как предположение о дифференцируемости функционала сделано, метод приводит к уравнениям в частных производных, что делает его неосуществимым. Но сила метода заключается в том, что он позволяет избежать аналитического решения и дает алгоритмы приближенного решения задачи путем расчленения её на этапы, на которых вычисляются участки оптимальных траекторий.

Однако в сложных случаях объем вычислительной работы при реализации такой процедуры часто оказывался непосильным даже для мощных компьютеров. Были найдены пути усовершенствования вычислительной процедуры для некоторых частных задач. Когда критерий оптимальности представляет собой квадратичный функционал относительно ошибки управления, задача сводится к обыкновенным нелинейным уравнениям типа Риккатти, методы решения которых известны. В других случаях уравнения решаются численными методами с числом операций, меньшим, чем в процедуре Беллмана.