10.4.Уравнения и передаточные функции дискретных систем
10.4.1.Уравнение и передаточная функция разомкнутой дискретной системы
Структурная схема разомкнутой дискретной системы с одним импульсным элементом выглядит следующим образом (рис.10.28):
Здесь
-
последовательность мгновенных импульсов
типа-функций,
модулированных непрерывным сигналом
;
-
передаточная функция приведенной
непрерывной части системы.
Проблема 1. необходимо найти уравнение, связывающее временные функции
на входе и на выходе разомкнутой дискретной системы, то-есть, найти уравнение разомкнутой дискретной системы во временной области.
Будем последовательно рассматривать реакцию приведенной непрерывной части
на последовательность мгновенных импульсов, приложенных к её входу.
1. Пусть на вход подан один импульс единичной площади (рис.10.29).
Рис. 10.29
2. На входе приведенной непрерывной части действует мгновенный импульс единичной площади, но сдвинутый на n периодов дискретизации (рис.10.30).
3. Теперь посмотрим реакцию ПНЧ на мгновенный импульс, смещенный на n
периодов и модулированный непрерывным сигналом ( рис.10.31).
Рис. 10.31
4.Наконец, посмотрим реакцию приведенной непрерывной части системы на последовательность мгновенных импульсов, модулированных непрерывным сигналом, (рис.10.32).
Рис. 10.32
По полученному
уравнению считают выходную переменную
для 
Тогда
уравнение
разомкнутой системы 
2. Вторая проблема – получить уравнение в -изображениях для разомкнутой системы.
Подвергнем
последнее уравнение -преобразованию:
Согласно теореме об изображении свертки
имеем
Обозначая 
,
имеем окончательно
Таким
образом получено уравнение в -изображениях
для разомкнутой дискретной системы.
-изображение
называется передаточной функцией
разомкнутой системы. Так как через
передаточную функцию можно найти
только ряд дискретных значений выходной величины, такую передаточную функцию называют дискретной передаточной функцией. Её находят двумя способами:
1.Используя обратное
преобразование Лапласа 
=
и затем подвергая -преобразованию:
;
2.Определяют
непосредственно
по
,
разлагая последнюю передаточную функцию
на ряд простых слагаемых.
Два
замечания по определению 
:
дискретная передаточная функция нескольких последовательно соединенных
непрерывных звеньев не равна произведению их передаточных функций (рис.10.33);
для схемы
рис. 10.33 справедливо 
дискретная передаточная функция параллельно соединенных элементов равна сумме передаточных функций отдельных элементов (рис.10.34).
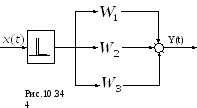
Для
схемы рис.10.34 имеем: 
где
10.4.2. Уравнение и передаточные функции замкнутой дискретной системы
Необходимо найти уравнение и передаточную функцию замкнутой дискретной системы с одним импульсным элементом (рис.10.35).
Запишем
уравнение разомкнутой системы: 
В этом уравнении
входной
сигнал 
есть
ошибка – разность между задающим
воздействием
и выход
ной величиной
:
Подвергнем ошибку преобразованию
Лапласа: 
Подставляем -преобразование ошибки в уравнение разомкнутой системы.
.
После
несложных преобразований получаем 
Из последнего выражения нетрудно получить формулу для передаточной функции замкнутой системы:
Отметим, что полученное выражение по форме полностью аналогично выражению передаточной функции замкнутой непрерывной системы.
Получим теперь выражение передаточной функции замкнутой системы по ошибке, то-есть, отношение изображений ошибки к изображению задающего воздействия.
Опять
подвергнем уравнение ошибки -
преобразованию:
Заменим в
этом уравнении
выражением:
=
.
Отсюда нетрудно получить выражение
передаточной функции по ошибке для замкнутой дискретной системы:
.
Видим, что полученное выражение передаточной функции полностью по форме
повторяет соответствующее выражение для непрерывной замкнутой системы.
10.4.3. Уравнения и передаточные функции дискретных систем произвольной структуры.
Дискретные системы управления, что мы рассматривали ранее, содержали один дискретный элемент, стоящий в прямом канале системы после узла сравнения. Однако, существует множество дискретных систем, где дискретный элемент расположен или в цепи обратной связи, или в середине прямой цепи, или сразу во многих точках замкнутых контуров.
Чтобы записывать уравнения в - изображениях в дискретных автоматических системах управления произвольной структуры, следует пользоваться тремя следующими правилами.
1. Если дискретный сигнал действует на группу непрерывных звеньев (рис. 10.36), то - изображение выходного сигнала
где
есть
символическое обозначение
2.
Если непрерывный сигнал действует на
входе одного или нескольких непрерывных
звеньев, то 
-изображение выходного сигнала (рис.10.37) будет равно:
где
есть
преобразование произведения непрерывных
изображений 
.
3. Третье правило устанавливает порядок записи уравнений в -изображениях, когда дискретный сигнал действует на группу непрерывных звеньев, разделенных
дискретными элементами, действующими синхронно (рис.10.38).
Изображение
выходного сигнала 
Используя выше сформулированные правила для записи уравнений в -изображениях, рассмотрим несколько конкретных примеров.
Система с импульсным датчиком (рис.10.39,а).
Чтобы написать уравнения, предварительно трансформируем исходную схему,
выполнив искусственный разрыв контура перед первым импульсным элементом (рис.10.39,б).
Рис.10.39
И окончательно,
можем написать 
Однако по этому выражению нельзя
написать передаточную функцию замкнутой
системы, так как нет свободного
-изображения
входного сигнала
.
2. Система с дискретизацией сигнала обратной связи (многоточечное регулирование) (рис.10.40,а).
В этом
случае, в преобразованной схеме (рис.
10.40,б) вводится промежуточная величина
,
для которой и записывается
- изображение:
-изображение
выходной величины
3. Система с дискретным элементом в середине прямого канала системы (рис.10.41,а).
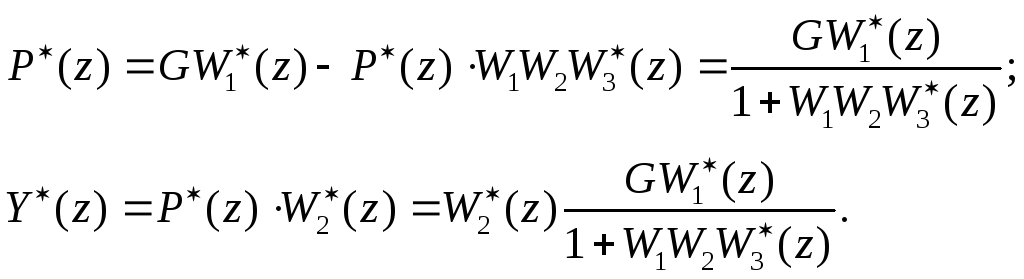
4. Система с цифровым контроллером в прямом канале системы (рис. 10.42,а).
В этой схеме: Е1- дискретный элемент, соответствующий преобразователю АД системы; Е2 – дискретный элемент, соответствующий преобразователю ДА системы.
Согласно
схеме, рис.10.42,б, напишем уравнения в
-изображениях,
сначала, для промежуточной величины
,
потом для выходной величины
.