10.3.3. Общие свойства z-преобразования
10.3.3.1. Правило линейности z-преобразования.
Определение: Z-преобразование линейной комбинации непрерывных функций
равно линейной комбинации их изображений
.
10.3.3.2. Правило смещения во временной области (теорема смещения).
Обычно различают два случая: смещение вправо (запаздывание) и смещение влево (опережение).
Правило смещения временной функции вправо (запаздывание): смещению функции-оригинала вправо на m интервалов дискретности соответствует умножение на
Z-преобразования
несмещенной временной функции
.
Приведенное
правило позволяет представить дискретный
фильтр или канал цифрового регулятора
в виде структурной схемы, где сдвиг на
один период дискретности соответствует
умножению сигнала на
(рис. 10.24)
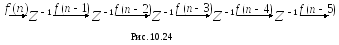
Правило смещения временной функции влево (опережение): смещению функции-оригинала влево на m интервалов дискретности соответствует умножение на
Z-преобразования
несмещенной временной функции, если m
значений временной
функции равны нулю:
10.3.3.3.
Правило умножения функции-оригинала
на
(теорема
демпфирования):
если некоторая функция
умножается на экспоненциальную функцию
.то
Z-преобразование
произведения вычисляется согласно
теореме демпфирования следующим образом
Пример использования теоремы
демпфирования для определенияZ-изображения
одной временной функции.
Определить
изображение функции
.
=
10.3.3.4. Правило умножения функции-оригинала на
Необходимо
определить изображение функции, имеющей
изображение
,
умноженной на
Правило умножения дает следующий
результат:
Правило
можно сформулировать с точностью до
множителя
следующим
образом:
умножению функции-оригинала на
соответствует взятие
производной
от изображения самой функции.
Пример применения правила.
Определить
изображение
.
10. 3.3.5. Правило определения изображения конечной разности К-порядка
Взятию
конечной разности К-порядка
от дискретной функции соответствует
умножение изображения функции на
.
10.3.3. 6. Правило определения изображения конечной суммы
Если
Значит, можно сформулировать правило
следующим образом: суммированию в
области временных дискретных функций
соответствует умножение изображения
исходной дискретной функции на
.
10.3.3.7. Теорема дискретной свертки
Определение свертки двух дискретных функций: сверткой двух дискретных
функций
называется дискретная функция
,
значения которой определяются следующим
выражением
=
Согласно теореме о дискретной свертке, изображение свертки двух дискретных
функций равно произведению изображений свертываемых функций.
Если
то
Теорема свертки чрезвычайно важна для вывода выражения передаточной функции дискретной системы.
10. 3.3.8. Связь между спектрами непрерывного и дискретного сигналов
Для установления связи между непрерывным и дискретным преобразованием
весьма полезным, оказывается знать связь между спектрами непрерывного и дискретного сигналов.
Как известно,
спектр непрерывного сигнала
определяется преобразованием Фурье
Следует заметить, что преобразование Фурье не может быть применено непосредственно к дискретной функции времени. Поэтому следует представить дискретный сигнал как сумму модулированных δ-функций:
-
последовательность единичных мгновенных
импульсов. Как показывает рис.10.25, эта
последовательность
периодическая с периодом, равным периоду дискретизации Т.
Каждая периодическая функция может быть разложена в ряд Фурье
-
коэффициент ряда Фурье
где
круговая частота квантования. Рассмотрим
функцию под знаком интеграла. Как видно
из рис.10.26, в пределах интегрирования
существует только одна δ-функция.
Поэтому для коэффициента ряда Фурье получим следующее выражение
Следовательно,
все коэффициенты ряда Фурье равны,
независимо от номера гармоники. Поэтому
для всей последовательности мгновенных
единичных импульсов справедливо
выражение
Для последовательности мгновенных импульсов, модулированных непрерывным сигналом, получим
К такому представлению дискретного сигнала преобразование Фурье допустимо:
где
смещенный спектр непрерывного сигнала.
Следовательно, спектр дискретного сигнала равен бесконечной сумме смещенных спектров непрерывного сигнала.