10.2.2. Эквивалентная схема дискретного элемента. Математическое его описание

Заметим, что решение и использование разностных уравнений высоких порядков

является трудным. Однако, прямое использование преобразования Лапласа, значительно упрощающего решение дифференциальных уравнений непрерывных систем, не может быть применено к дискретным функциям, не удовлетворяющим исходным требованиям преобразования Лапласа.

Поэтому во временной области используют представление дискретных функций с

помощью - функций, являющихся непрерывными функциями времени.

С этой целью вводится понятие об абстрактном дискретном элементе, заменяющего реальный дискретный элемент последовательным соединением идеального импульсного элемента (ИИЭ) и формирующего звена (ФИ), восстанавливающем реальную форму импульсов (рис. 10.17).

На рис.10.17:

- последовательность выходных импульсов идеального импульсного элемента;

- последовательность выходных импульсов реального импульсного элемента.

Идеальным импульсным элементом называется абстрактный элемент, который под действием непрерывного сигнала на его входе генерирует мгновенные импульсы типа -функций, которые следуют с периодом, равным периоду реального дискретного элемента, и по площади равны значениям непрерывного сигнала в моменты времени, непосредственно предшествующие моментам появления импульсов.

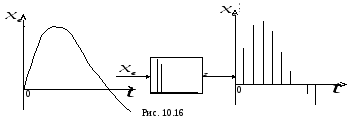
Рис. 10.16 отражает процесс преобразования непрерывного сигнала в последовательность модулированных по площади -функций.

Идеальный импульсный элемент позволяет также представить преобразование

непрерывного сигнала в последовательность цифровых значений. При этом, площадь дельта функций равна цифровым значениям в соответствующие моменты квантования.

Это преобразование показано графически на рис.10.17.

-функцией называется функция , удовлетворяющая следующим условиям:

1. 2. .

Согласно этим условиям импульс типа -функции должен иметь амплитуду,

равную бесконечности. На рисунках принято представлять мгновенные импульсы с конечной амплитудой, равной площади -функции. На рис.10.18 показана последовательность-функций единичной площади.

-функция в момент времени обозначается- функции, появляющиеся

в моменты времени , записываются как

Вся последовательность -функций единичной площади будет представляться так:

Последовательность мгновенных импульсов на выходе идеального импульсного

элемента может рассматриваться как результат модуляции последовательности

непрерывным сигналом (рис. 10.19)

Исходя из рис.10.19 следует, что

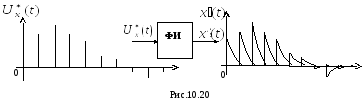
Переходим к описанию формирующего элемента. Напомним, что формирующий

элемент формирует реальные импульсы под влиянием мгновенных импульсов типа

-функций на его входе (рис.10.20).

Вспомним, что реакция любого элемента на - функцию называется его весовой функцией или импульсной переходной характеристикой. Это значит, что можно определить описание формирующего элемента как его импульсную переходную характеристику. Известно также, что преобразование Лапласа импульсной переходной характеристики есть передаточная функция элемента, на выходе которого появляется

импульсная переходная характеристика.

Следовательно, можно определить математическое описание формирующего элемента, подвергая преобразованию Лапласа функцию, описывающую реальный импульс дискретного элемента.

В качестве примера определим передаточную функцию фиксатора нулевого

порядка.

Сначала определим преобразование Лапласа функции, описывающей прямоугольный импульс длительностью , где -период дискретизации и  - относительное значение длительности импульса по отношению к периоду (рис.21).

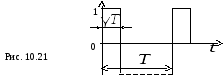
Для импульсной переходной характеристики элемента имеем

Преобразуем эту функцию по Лапласу:

Первый интеграл равен Определяем второй интеграл

И окончательно имеем

Рассмотрим два частных случая: 1) =1; 2) «1.

В первом случае мы имеем импульс на выходе экстраполятора 0-го порядка. В этом случае

Во втором случае имеем дискретный элемент без запоминания

Можно доказать это выражение разлагая в ряд Маклорена по возрастающим степеням :

Достаточно оставить два первых члена разложения в ряд: Подставляя

это выражение в общее выражение передаточной функции прямоугольного импульса,

получаем

Возможность определить передаточную функцию формирующего элемента позволяет отнести её к непрерывной части системы (рис. 10. 22).

Непрерывная часть системы при этом будет называться приведенной (ПНЧ).