10.1.4. Классификация дискретных элементов

Принято делить все дискретные элементы в соответствии с длительностью процесса квантования и в соответствии с наличием или отсутствуем запоминания сигнала на часть или на весь период квантования.

В соответствии с длительностью процесса квантования делят дискретные элементы на две группы: - элементы 1-го рода; - элементы 2-го рода. Для элемента 1-го

рода длительность квантования чрезвычайно мала по сравнению с периодом квантования, как показывает рис. 10.7.

Часто дискретный элемент 1-го рода называют идеальным дискретным элементом. Особенно, если речь идет о преобразовании непрерывного сигнала в последовательность цифровых значений, как показывает рис. 10.8.

Отметим, что графическое обозначение идеального дискретного элемента это нормально открытый контакт реле, снабженный стрелкой.

У дискретного элемента 2-го рода длительность каждого импульса лишь немного

меньше периода дискретизации, как показано на рис. 10.9.

Элемент 2-го рода часто называют реальным дискретным элементом. В моделях элемент 2-го рода обозначают контактом реле без стрелки, как свидетельствует рис.10.11.

Элементы с запоминанием запоминают последнее значение непрерывного сигнала при каждом акте квантования или на часть периода, или на весь период дискретизации. Рис. 10.12 и 10.13 иллюстрируют эффект запоминания для элемента 1-го рода (рис.10.12) и для элемента 2-го рода (рис. 10.13).

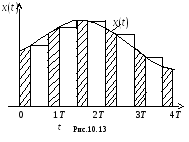
Для элемента 1-го рода с запоминанием на весь период дискретизации в дальнейшем используем название «экстраполятор нулевого порядка». Его графическое

обозначение показано на рис. 10.14.

10.2. Описание дискретных сигналов во временной области

10.2.1. Дискретные функции времени и уравнения в конечных разностях

В общем случае, дискретная функция это функция дискретного аргумента. Если аргументом является время, то речь идет о дискретной функции времени. Обозначение

дискретной функции времени таково:

где - число периодов дискретизации, прошедших с начала отсчета. Графическое представление дискретной функции времени показано на рис. 10.15.

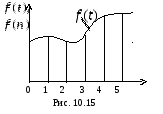
Отметим, что имеющейся непрерывной функции при фиксированномсоответствует одна дискретная функция тогда как для данной дискретной функции времени можно сопоставить множество непрерывных функций, имеющих одинаковые дискретные значения. Это положение иллюстрирует

рис. 10.16.

Локальные свойства дискретных функций времени характеризуют с помощью конечных разностей. Дискретной разностью 1-го порядка называют дискретную функцию, определяемую следующим образом:

Дискретной разностью го порядка называется дискретная функция

На рис 10.16 показаны разности первого порядка:

для

,

для

Чтобы характеризовать интегральные свойства дискретных функций используют понятие конечной суммы:

.

Необходимо отметить, что между интегралом и конечной суммой имеется существенная разница, а именно: конечная сумма не зависит от перемены пределов суммирования, тогда как интеграл непрерывной функции меняет свой знак с переменой пределов интегрирования.

Уравнение, связывающее дискретные функции и их конечные разности разных порядков, называется разностным уравнением:

Разностные уравнения широко используются для записи алгоритмов управления

цифровых управляющих устройств (контроллеров).