10.8. Анализ дискретных систем в установившихся режимах

10.8.1.Анализ точности дискретных систем в установившихся режимах

Точность работы дискретной системы в установившемся режиме может быть оценена ошибкой, вызванной изменением управляющего воздействия.

Возможно, определить ошибку в установившемся режиме с помощью зависимости, связывающей дискретную временную функцию во временной области и изображение ошибки

,

при условии, что все особые точки (полюса) находятся внутри круга единичного радиуса.

Известно, что значение ошибки в установившемся режиме, зависит от типа сигнала, приложенного к входу системы, а также параметров системы. Эта зависимость выражается коэффициентами ошибок, аналогичными соответствующим коэффициентам непрерывных систем.

Возьмем в качестве примера базовую структурную схему дискретной системы с одним дискретным элементом (рис. 10.58.)

z-изображение ошибки для этой системы

Рассмотрим три частных случая:

1. где - управляющий сигнал - ступенька положения

2. управляющийсигнал– ступенькаскорости

3. управляющийсигнал–ступеньускорения

1. Сигнал управления – ступенчатый скачок положения Подставим выражение сигнала управления в формулу ошибки

Ошибкавустановившемсярежиме

Пусть общий коэффициент передачи разомкнутой системы. Имеем тогда

коэффициент ошибки по положению.

Из ошибки по положению вытекает, что будет при условии, что это означает, что передаточная функция должна иметь, по меньшей мере, один полюс z=1, то-есть, передаточную функцию дискретного интегратора

2. Управляющий сигнал - скачок скорости

Определим ошибку в установившемся режиме, вызванную скачком скорости, приложенным к входу системы. Ошибку в установившемся режиме, вызванную скачком скорости на входе системы, определим, подставив - преобразование скачка скорости в общее выражение  - преобразования ошибки:

изображения ошибки

Для ошибки во временной области получим:

Определим коэффициент ошибки отработки скачка скорости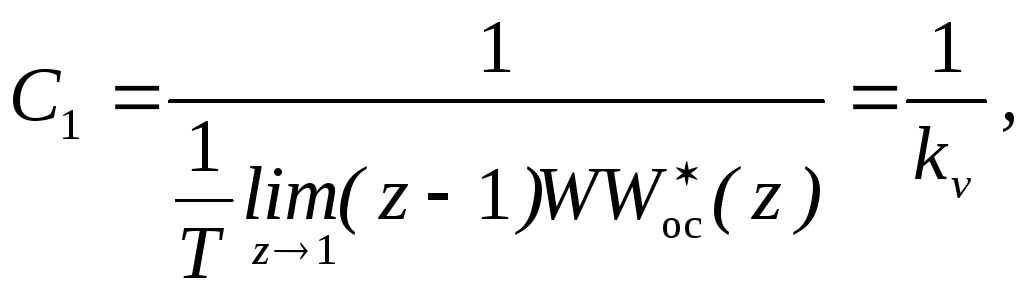

где постоянная величина режима скорости (фактор качества отработки скачка скорости дискретной системой). Окончательно, имеем для ошибки в временной области

Следует отметить, что выражение ошибки, полученной выше, справедливо

только, если управляющий сигнал есть скачок скорости.

Из этого следует, что будет равен бесконечности, если передаточная функция

имеет два полюса z=1.

3. Управляющий сигнал – скачок ускорения

-преобразование скачка ускорения таково:

и -изображение ошибки, вызванной скачком ускорения

Для ошибки в установившемся режиме временной области имеем:

Окончательно, запишем: где a – ускорение управляющего сигнала,

C₂ – коэффициент ошибки ускорения.

- коэффициент ошибки по

ускорению.

Так же, как в предыдущих случаях выражение C₂ справедливо только при

условии, что сигнал на входе системы это скачок ускорения.

В заключение, надо подчеркнуть, что, если управляющий сигнал равен сумме трех составляющих: скачка положения, скачка скорости и скачка ускорения –

ошибка в установившемся режиме есть функция коэффициентов самой дискретной системы:

положения;

скорости,

-ускорения.