10.7.2.Построение логарифмических характеристик интегрирующего звена

Структурная схема элемента представлена на рис. 10.51.

Схема содержит идеальный импульсный элемент, экстраполятор 0-го порядка и непрерывный интегратор. Два непрерывных элемента объединены в приведенную непрерывную часть (ПНЧ).

Передаточная функция приведенной непрерывной части

Дискретная передаточная функция ПНЧ:

Делаем подстановку

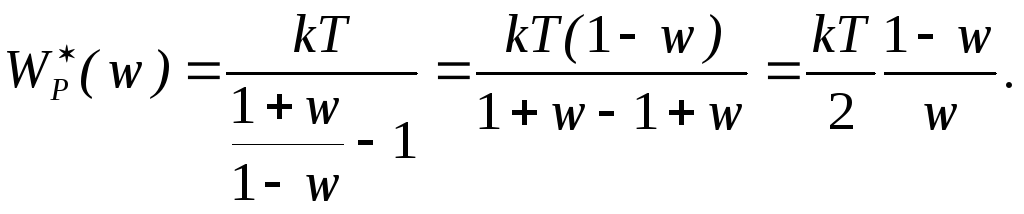
Подставим вместо . Имеем тогда

Выражение логарифмической АЧХ:

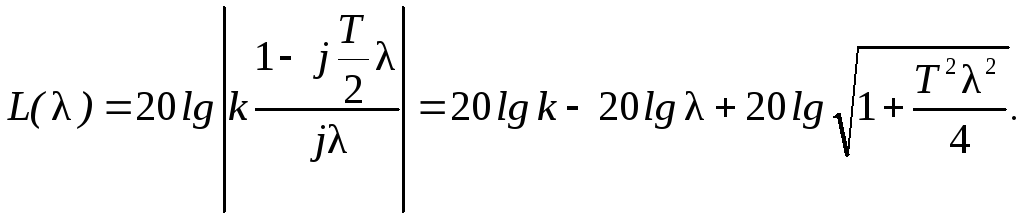
Выражение логарифмической ФЧХ: ()=-arctg .

Построение характеристик выполнено на рис. 10.52.

Следует отметить, что характеристики et () совпадают полностью с характеристиками непрерывного интегратора в области низких частот. Разница появляется лишь на высоких частотах.. ФЧХ стремится к -180^о , что означает снижение запаса устойчивости по сравнению с непрерывными системами.

Важно также отметить, что совпадение характеристик на низких частотах позволяет перенести на дискретные системы оценки, сделанные для непрерывных систем в установившихся режимах.

10.7.3. Построение логарифмических характеристик апериодического элемента с реальным дискретным элементом.

Начальная структурная схема показана на рис.10.53,а.

Можно заменить структурную начальную схему, схемой, состоящей из идеального импульсного элемента, экстраполятора 0-го порядка и непрерывного периодического элемента (рис.10.53,b).

Приходим к окончательной приведенной структурной схеме, показанной на рис. 10.54.

Построение логарифмических характеристик содержит следующие операции:

1. определение дискретной передаточной функции;

2. w- преобразование передаточной функции, полученной на первой операции;

3. вывод выражений логарифмических характеристик дискретной системы;

4. построение кривых АЧХ и ФЧХ в логарифмическом масштабе для конкретных значений параметров системы: k, T ₁et T (период дискретизации).

Первая операция.

Дискретная передаточная функция получается -преобразованием непрерывной передаточной функции с учетом экстраполятора 0-го порядка:

Чтобы найти  - преобразование выражения используют разложение на простые дроби :

Z- преобразование

Подставляя это преобразование в общее выражение , получаем

Вторая операция.

Подставляем в выражение передаточной функции и ,после нескольких преобразований, приходим к передаточной функции от w.

где .

Третья операция.

Подставляя в выражение , получаем

Нетрудно доказать, что

Таким образом, можно написать, окончательно

Четвертая операция.

Переходя к логарифмическим характеристикам, имеем

Графики ЛАЧХ и ЛФЧХ представлены на рис.10.55.

10.7.4. Построение логарифмических характеристик инерционного интегратора с реальным дискретным элементом

На рис.10.56,а показана схема изучаемого элемента. Заменяя реальный элемент комбинацией идеального импульсного элемента, экстраполятора 0-го порядка и собственно непрерывного элемента, приходим к эквивалентной схеме (рис.10.56,б).

Дискретная передаточная функция

Делаем, как и раньше, разложение на простые дроби:

Имеем , следовательно,

Переходя к -преобразованиям, находим

Для общей передаточной функции получим:

Вводим W-преобразование, заменяя z на z=(1+w)/(1-w).

Приводим выражение в скобках к общему знаменателю

Приводим теперь выражение в квадратных скобках к форме

Получаем окончательно выражение передаточной функции:

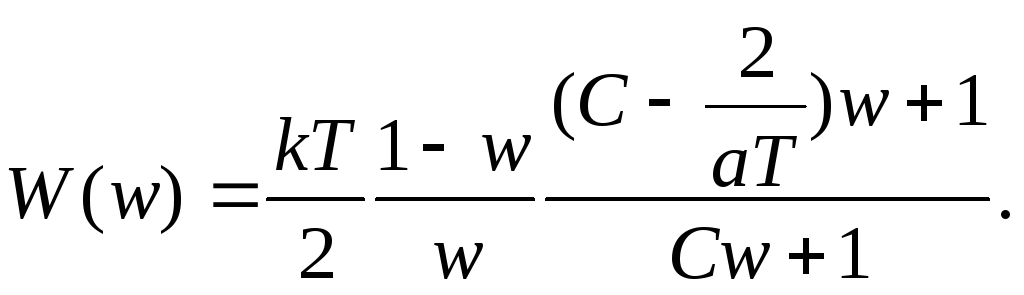
Подставляя в приходим к выражению в функции абсолютной псевдочастоты λ:

Запишем окончательно выражения логарифмических характеристик ЛАФЧХ :

Можно видеть, что стремится кT ₁ , когда t идет к нулю, но не становится точно равно T _1. Приравняем ≈ T ₁ в знаменателе, тогда как в числителе необходимо рассчитать разность , которой нельзя пренебречь. Построение характеристикпоказано на рис. 10.57.