
- •10. Дискретные системы управления
- •10.1. Терминология и классификация элементов дискретных систем
- •10.1.1 Общая терминология дискретных систем
- •10.1.2. Типы квантования в дискретных системах
- •10.1.3. Виды модуляции в дискретных системах
- •10.1.4. Классификация дискретных элементов
- •10.2. Описание дискретных сигналов во временной области
- •10.2.1. Дискретные функции времени и уравнения в конечных разностях
- •10.2.2. Эквивалентная схема дискретного элемента. Математическое его описание
- •10.3. Дискретное преобразование Лапласа. Z-преобразование и его свойства
- •10.3.1. Дискретное преобразование Лапласа
- •10.3.3. Общие свойства z-преобразования
- •10.3.3.1. Правило линейности z-преобразования.
- •10.3.3.2. Правило смещения во временной области (теорема смещения).
- •10.3.3.4. Правило умножения функции-оригинала на
- •10.3.3.9. Связь между z- преобразованием и непрерывным преобразованием Лапласа
- •10.3.3.10. Обратное z-преобразование
- •10.4.Уравнения и передаточные функции дискретных систем
- •10.4.1.Уравнение и передаточная функция разомкнутой дискретной системы
- •10.4.2. Уравнение и передаточные функции замкнутой дискретной системы
- •10.5. Частотные характеристики дискретных систем
- •10. 6. Исследование устойчивости дискретных систем
- •10.6.1.Общий критерий устойчивости дискретных систем
- •10.6.2.Алгебраические критерии устойчивости дискретных систем
- •10.6.2.1. Аналог критерия Гурвица
- •10.6.2.2. Алгебраический критерий Джури
- •10.6.2.3.Критерий устойчивости Шура - Кона
- •10.6.3. Амплитудно-фазовый критерий устойчивости замкнутых дискретных систем (критерий Найквиста)
- •10.6.4. Критерий характеристического полинома устойчивости замкнутых дискретных систем.
- •10.7. Построение логарифмических амплитудно-частотных (лачх) и фазочастотных характеристик(фчх) разомкнутых дискретных систем
- •10.7.1. Связь между круговой частотой ω и аргументом w-преобразования
- •10.7.2.Построение логарифмических характеристик интегрирующего звена
- •10.7.3. Построение логарифмических характеристик апериодического элемента с реальным дискретным элементом.
- •10.7.4. Построение логарифмических характеристик инерционного интегратора с реальным дискретным элементом
- •10.8. Анализ дискретных систем в установившихся режимах
- •10.8.1.Анализ точности дискретных систем в установившихся режимах
- •1. Сигнал управления – ступенчатый скачок положения Подставим выражение сигнала управления в формулу ошибки
- •10.8.2. Влияние порядка астатизма и периода дискретизации на ошибки в установившемся режиме
- •10.8.4. Выбор частоты дискретизации
10. Дискретные системы управления
10.1. Терминология и классификация элементов дискретных систем
10.1.1 Общая терминология дискретных систем
Дискретной системой называют любую систему, имеющую дискретный характер передачи сигналов в прямом или в обратном канале системы. Дискретность сигналов может быть обусловлена использованием цифровых приборов управления,
коммутацией сигнала при многоканальном или многомерном управлении. Часто такие системы управления называют цифровыми системами.
С другой стороны, получают дискретный характер передачи, используя преобразование непрерывных сигналов с помощью контактов реле или электронных
устройств. Такие системы называют импульсными АСУ.
10.1.2. Типы квантования в дискретных системах
В дискретных системах, независимо от их физической природы, осуществляют
преобразование непрерывных сигналов в последовательность импульсов или цифровых значений. Преобразование непрерывного сигнала в дискретный называют квантованием
или дискретизацией непрерывного сигнала.
Различают три типа квантования:
- квантование по времени;
- квантование по уровню;
- смешанное квантование по времени и по уровню.
При квантовании по времени непрерывный сигнал заменяется последовательностью импульсов или цифровых значений, параметры которых (амплитуда, длительность импульса или их фазовый сдвиг) равны значениям непрерывного сигнала в моменты преобразования, следующие через равные промежутки времени. Называют время между двумя соседними моментами квантования
периодом квантования и обозначают заглавной буквой Т (рис. 10.1).

При квантовании по уровню из непрерывного сигнала извлекаются значения, совпадающие с тем или иным уровнем квантования. Этот процесс показан на рис. 10.2.

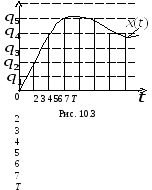
Наконец, смешанное квантование, когда используют квантование по времени, но
в качестве дискретных значений берут значения, близкие тому или иному уровню квантования, как это показано на рис. 10.3.
10.1.3. Виды модуляции в дискретных системах
Различают в дискретных системах следующие виды модуляции непрерывным сигналом последовательности импульсов или цифровых значений:
- амплитудно-импульсная модуляция;
- широтно-импульсная модуляция;
- фазоимпульсная модуляция;
- частотно-импульсная модуляция.
Амплитудно-импульсная модуляция это такой вид преобразования непрерывного сигнала в дискретный сигнал, амплитуда или цифровое значение которого соответствует значению непрерывного сигнала в момент квантования. Графическое представление такой модуляции показано на рис. 10.4.
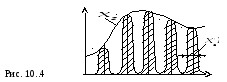
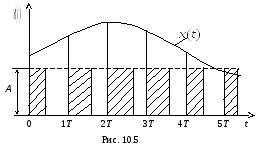
Широтно-импульсная модуляция заключается в том, что длительность импульсов
в моменты квантования определяется значениями непрерывного сигнала, как это показано на рис. 10.5.
Фазоимпульсной модуляцией называется такой вид преобразования непрерывного сигнала в дискретный сигнал, при котором сдвиг по фазе между двумя последовательностями импульсов или цифровых значений является функцией непрерывного сигнала в моменты квантования. Механизм такого преобразования показан на рис. 10.6.

На рис.10.6 А- амплитуда импульсов опорной последовательности; А1- амплитуда
рабочей последовательности импульсов; φ-сдвиг по фазе между импульсами двух последовательностей.
Частотно-импульсная модуляция состоит в том, что при постоянных амплитуде
и широте импульсов частота дискретизации есть функция непрерывного сигнала в моменты дискретизации. Механизм такого преобразования показан на рис. 10.7.
