
- •Построение и анализ
- •1. Графы. Основные определения
- •Графы. Основные определения
- •Графы. Основные определения
- •Графы. Основные определения
- •Графы. Основные определения
- •Графы. Основные определения
- •Отличие соответствия от функции
- •Графы. Основные определения
- •Графы. Основные определения
- •Графы. Основные определения
- •Графы. Основные определения
- •Графы. Основные определения
- •2. Представления графов
- •Представления графов
- •Представления графов
- •Представления графов
- •Списки смежности
- •Представления графов
- •Представления графов
- •Представления графов
- •Различные изображения графа. Пример 1.
- •Различные изображения графа. Пример 2.
- •Пример 2.
- •Множества вершин и ребер
- •Множества смежности
- •Списки смежности
- •Конец вводной части
- •3. Минимальное остовное дерево
- •Остовные деревья (леса)
- •Пример: решетчатый граф
- •Рассмотрим простой вариант задачи связности
- •Пример
- •Алгоритм
- •Пример работы алгоритма
- •Тот же граф
- •Реализация:
- •Вход:
- •Пример
- •Пример (конец)
- •Вход:
- •Реализация:
- •Реализация:
- •Пример
- •Вход:
- •Вход:
- •Минимальное остовное дерево
- •Продолжение задачи «Построение МОД» на следующей лекции
- •КОНЕЦ ЛЕКЦИИ

Пример: решетчатый граф
Картинка из «Седжвик, ч.1-4»
17.03.2014 |
Алгоритмы на графах |
31 |
|
Начало |
|

Рассмотрим простой вариант задачи связности
Предъявляется последовательность ребер графа: i1 – j1, i2 – j2, i3 – j3,…, im – jm
•Если для очередного ребра i – j оказывается, что в графе нет пути из i в j,
то ребро добавляется в результат.
•Если же уже есть путь из i в j, то ребро игнорируется.
Ясно, что так будет сформировано множество ребер
остовного дерева графа (или остовного леса).
17.03.2014 |
Алгоритмы на графах |
32 |
|
Начало |
|
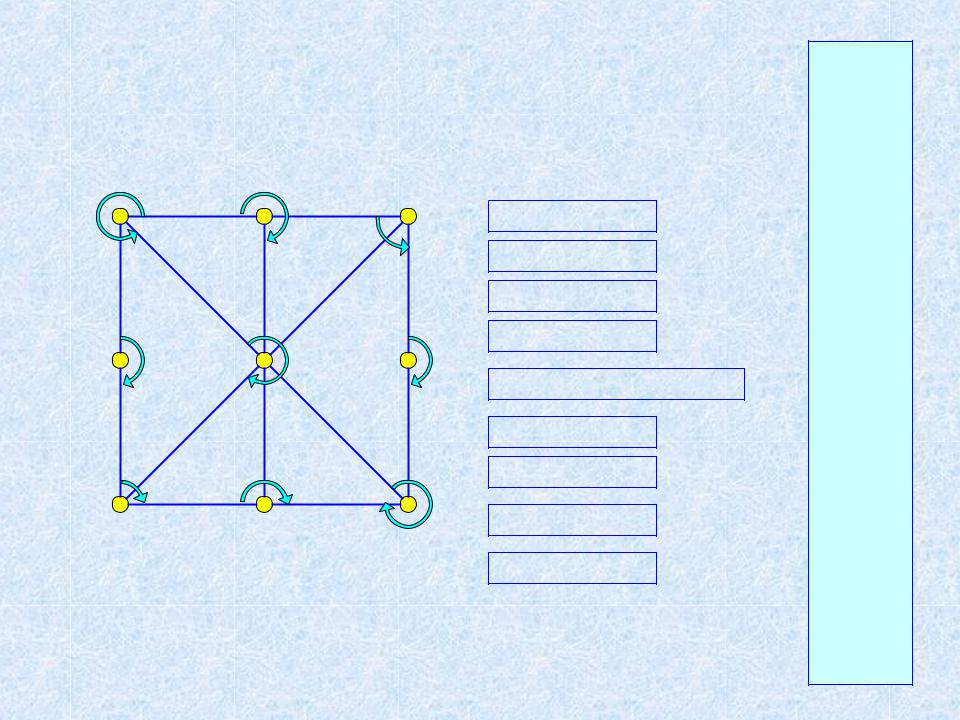
|
|
|
Пример графа |
|
|
|
|
(n = 9; m = 14) |
|
1 |
2 |
|
3 |
Adj[1]: 2, 4, 5 |
|
|
|
|
|
|
|
|
|
Adj[2]: 1, 3, 5 |
|
|
|
|
Adj[3]: 2, 5, 6 |
4 |
5 |
|
6 |
Adj[4]: 1, 7 |
|
Adj[5]: 1, 2, 3, 9, 8, 7 |
|||
|
|
|
|
|
|
|
|
|
Adj[6]: 3, 9 |
|
|
|
|
Adj[7]: 4, 5, 8 |
7 |
|
8 |
9 |
Adj[8]: 7, 5, 9 |
|
|
|||
|
|
|
||
Adj[9]: 5, 6, 8
17.03.2014 |
Алгоритмы на графах |
|
Начало |
Ребра: {1, 2} {1, 4} {1, 5} {2, 3} {2, 5} {3, 5} {3, 6} {4, 7} {5, 7} {5, 8} {5, 9} {6, 9} {7, 8} {8, 9}

Пример
Идея: пусть на некотором шаге сформирован остовный лес (выделены подмножества вершин – деревья остовного леса – W1, W2, …, WL).
Тогда при добавлении ребра:
•либо ребро соединяет вершины одного дерева (тогда образуется цикл) и такое ребро отбрасываем,
•либо ребро соединяет вершины разных деревьев Ws и Wt и тогда следует объединить Ws и Wt в одно множество.
17.03.2014 |
Алгоритмы на графах |
34 |
|
Начало |
|

Алгоритм
for (i = 1; i <= n ; i++) Wi = i;
// Все деревья – изолированные вершины while (cin >> p>> q)
{
Найти такие i и j , что p Wi и q Wj ; if (i == j) ничего
else {
cout << p <<‘ ‘<< q<< endl;
Объединить Wi и Wj
}
}
Операции НАЙТИ (Wi такое, что p Wi) и ОБЪЕДИНИТЬ (Wi и Wj )
17.03.2014 |
Алгоритмы на графах |
35 |
|
Начало |
|
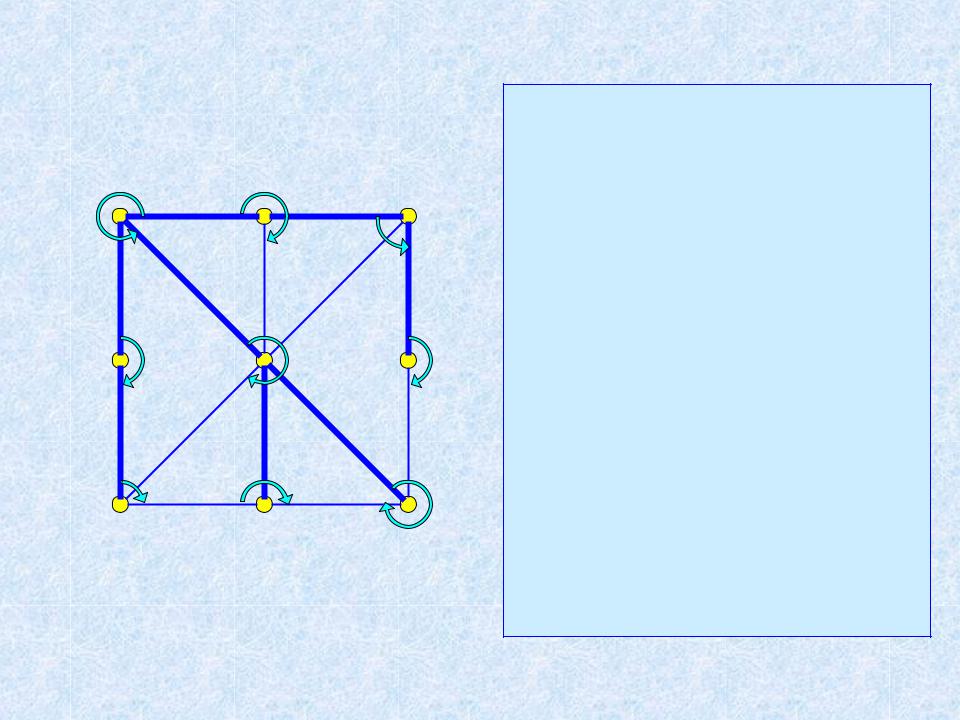
Пример работы алгоритма
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Лес: {1} {2} {3} {4} {5} {6} {7} {8} {9}
{1, 2} {1,2} {3} {4} {5} {6} {7} {8} {9} {1, 4} {1,2,4} {3} {5} {6} {7} {8} {9} {1, 5} {1,2,4,5} {3} {6} {7} {8} {9} {2, 3} {1,2,4,5,3} {6} {7} {8} {9} {2, 5} {3, 5}
{3, 6} {1,2,4,5,3,6} {7} {8} {9} {4, 7} {1,2,4,5,3,6,7} {8} {9} {5, 7} {5, 8} {1,2,4,5,3,6,7,8} {9}
{5, 9} {1,2,4,5,3,6,7,8,9} {6, 9} {7, 8} {8, 9}
17.03.2014 |
Алгоритмы на графах |
36 |
|
Начало |
|
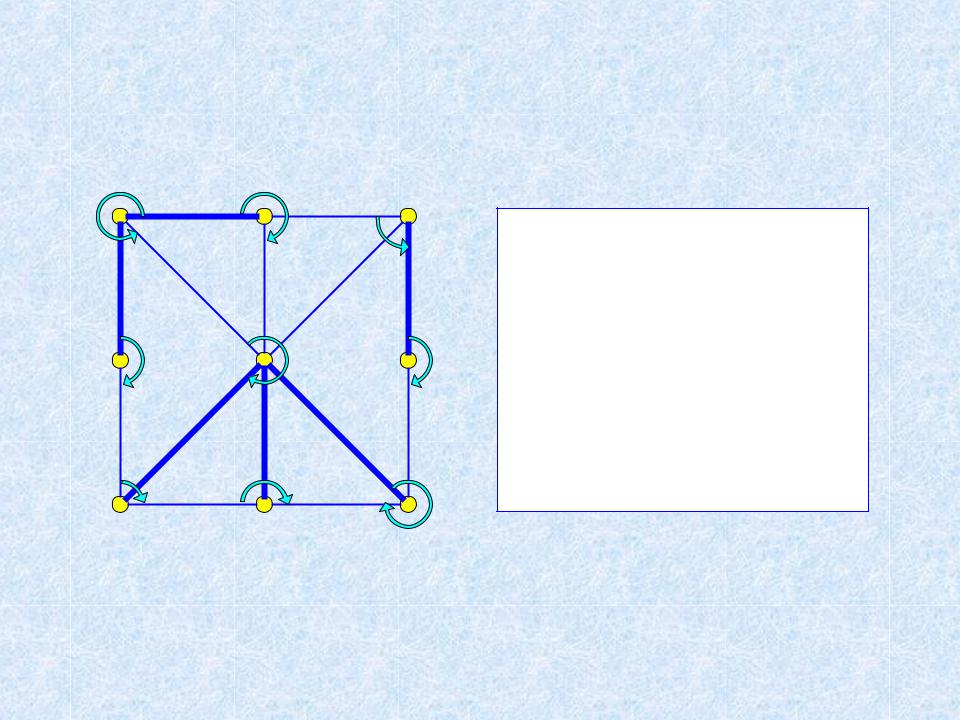
Тот же граф
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
При другом порядке предъявления ребер:
{1,2,4} {3,6} {5,7,8,9}
17.03.2014 |
Алгоритмы на графах |
37 |
|
Начало |
|

Реализация:
быстрый поиск – медленное объединение
int i, j, k, p, q, w[N];
for (i = 0; i < N; i++) w[i] = i; // w[i] – метка дерева
while
cout << "+ребро: " << p << " " << q << endl;
}
17.03.2014 |
Алгоритмы на графах |
39 |
|
Начало |
|

Вход: |
|
Выход: |
Пример |
|
|
|
12
14
3 6
5 8
5 7
5 9
7 8
8 9
2 5
2 3
15
3 5
4 7
6 9
Реализация:
быстрый поиск – медленное объединение
См. далее
17.03.2014 |
Алгоритмы на графах |
40 |
|
Начало |
|
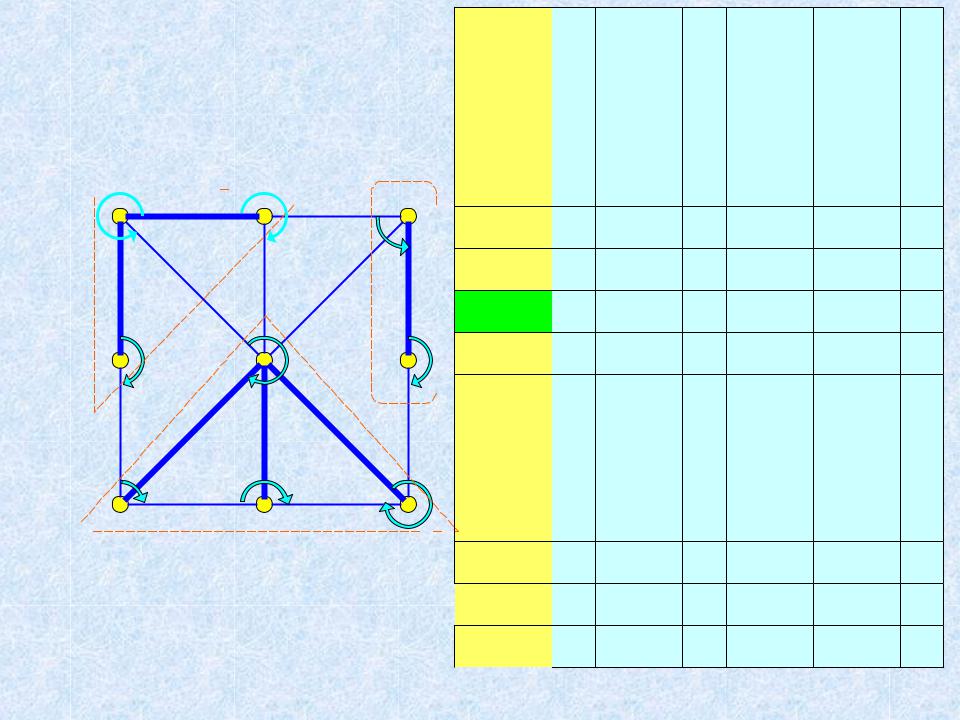
Пример
1










 2
2






4 |
5 |
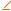
 7 8
7 8
|
|
|
|
|
Иниц. |
|
|
|
|
|
W[*]: |
|
|
|
|
|
1-2 |
|
|
|
|
|
1-4 |
3 |
|
3-6 |
|||
|
|
|
|
|
5-8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5-7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5-9 (!) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
7-8 |
|
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|||||
|
|||||
|
|
|
|
|
8-9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2-5 |
|
|
|
|
|
2-3 |
|
9 |
|
1-5 |
||
|
|
||||
|
|
|
|
|
3-5 |
 4-7 6-9
4-7 6-9
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
2 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
4 |
4 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
4 |
4 |
6 |
4 |
5 |
6 |
7 |
8 |
9 |
4 |
4 |
6 |
4 |
8 |
6 |
7 |
8 |
9 |
4 |
4 |
6 |
4 |
7 |
6 |
7 |
7 |
9 |
4 |
4 |
6 |
4 |
9 |
6 |
9 |
9 |
9 |
9 |
9 |
6 |
9 |
9 |
6 |
9 |
9 |
9 |
6 |
6 |
6 |
6 |
6 |
6 |
6 |
6 |
6 |
17.03.2014 |
Алгоритмы на графах |
41 |
|
Начало |
|
