
- •Построение и анализ
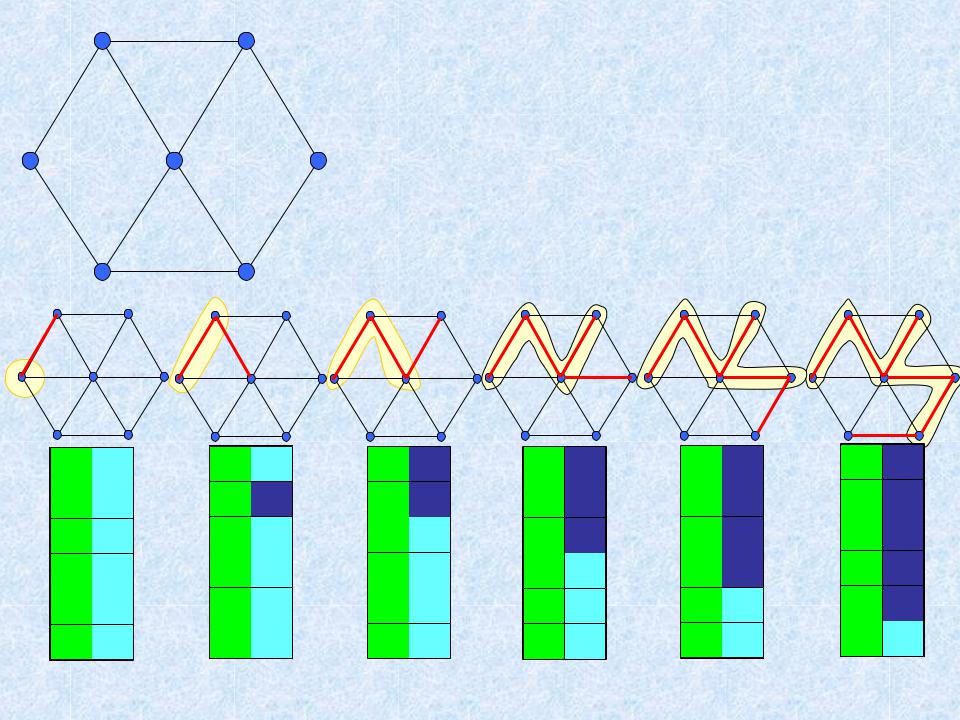
- •Остовное дерево
- •Остовное дерево
- •Минимальное остовное дерево (МОД)
- •1. Теорема о минимальном ребре. Версия
- •1. Теорема о минимальном ребре. Версия
- •1. Теорема о минимальном ребре. Версия
- •1. Теорема о минимальном ребре. Версия
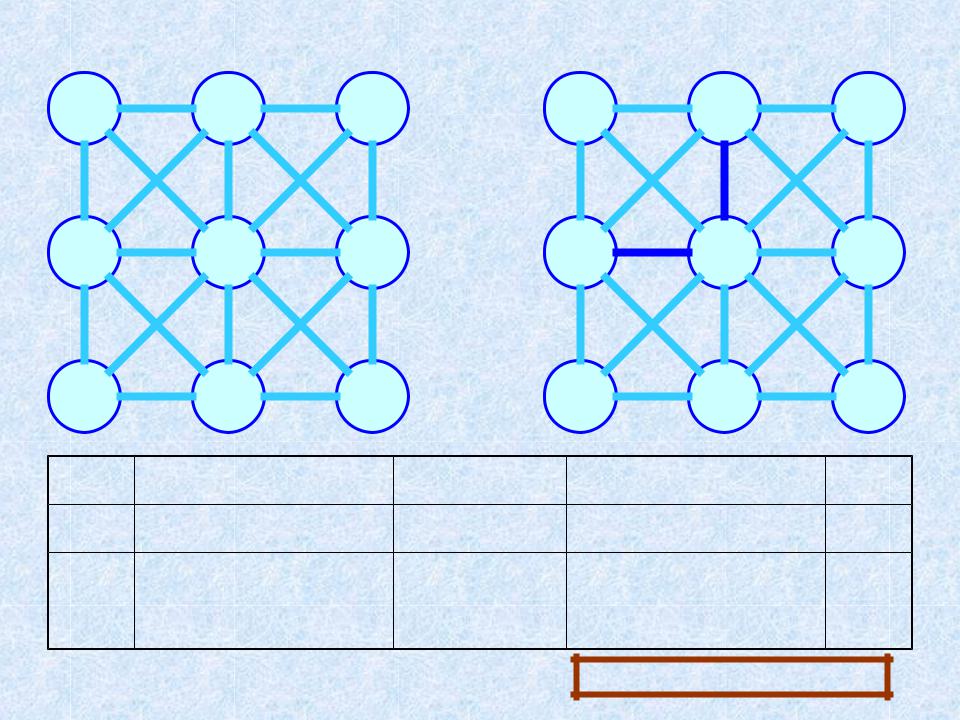
- •Теорема о минимальном ребре
- •Теорема о минимальном ребре
- •Алгоритмы построения МОД
- •«Краскал – Крускал»
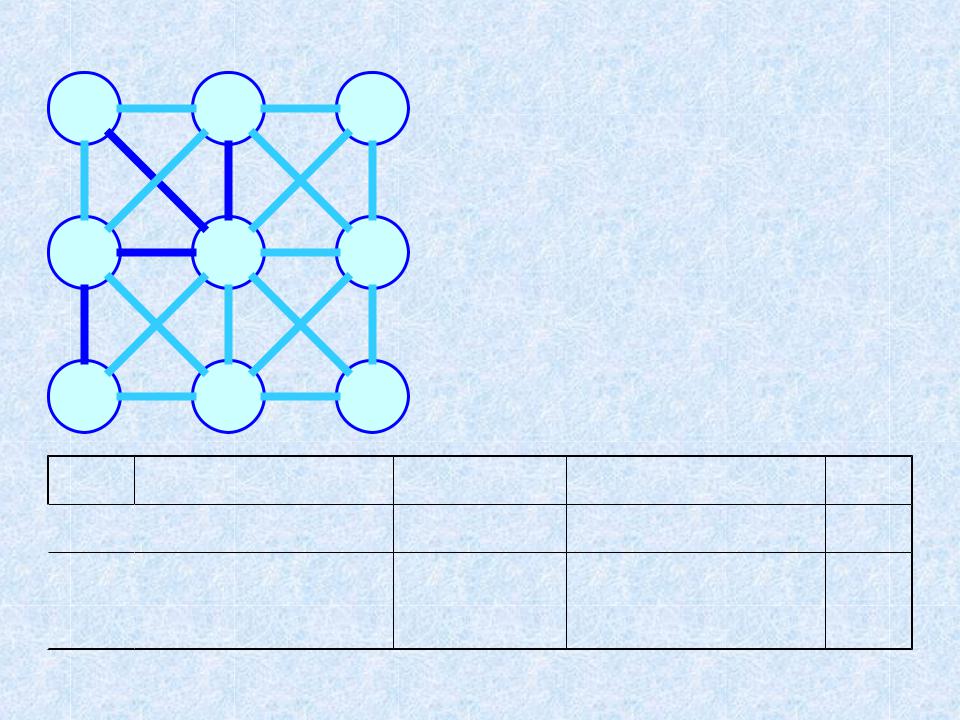
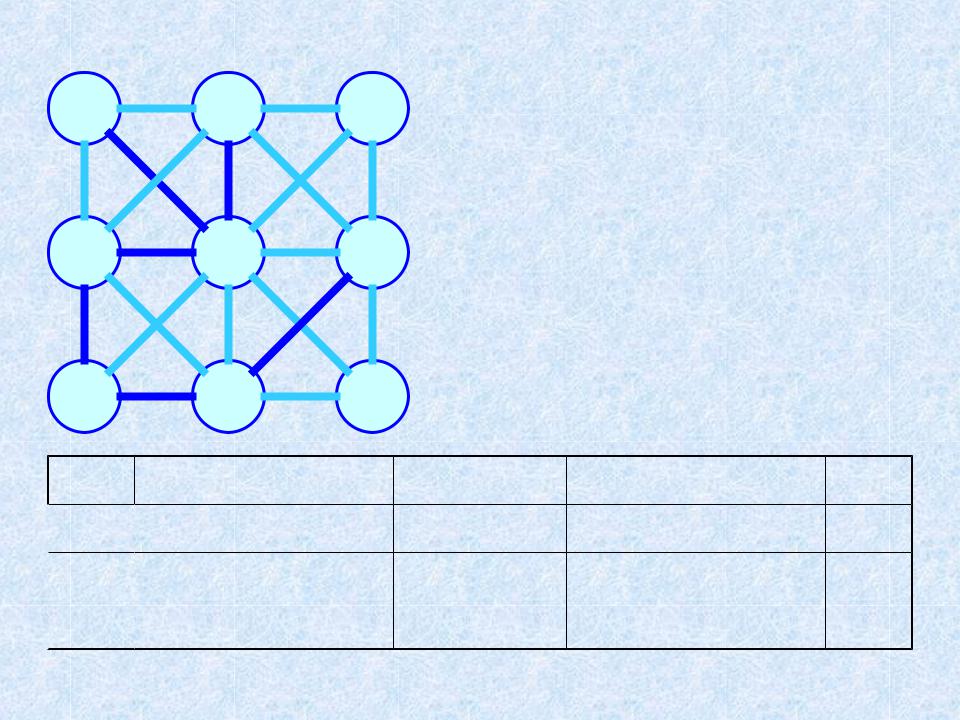
- •2. Жадный алгоритм построения МОД (Kruskal,
- •Жадный алгоритм построения МОД (Kruskal,
- •Жадный алгоритм построения МОД (Kruskal,
- •3. Алгоритм Ярника-Прима-Дейкстры построения
- •Алгоритм Ярника-Прима-Дейкстры
- •Алгоритм Ярника-Прима-Дейкстры
- •Алгоритм Ярника-Прима-Дейкстры
- •Алгоритм Ярника-Прима-Дейкстры
- •4. Нижняя граница задачи нахождения МОД
- •Реализация алгоритма Ярника-Прима-Дейкстры для разреженных графов
- •Алгоритм Ярника-Прима-Дейкстры построения МОД
- •Пример 1. МОД.
- •Пример выполнения алгоритма Ярника-Прима-Дейкстры
- •КОНЕЦ ЛЕКЦИИ

Алгоритм Ярника-Прима-Дейкстры
{Детализация фрагмента ф1:} min := + ;
for x (V \ Vt) do
if D [x,Near[x]] < min then begin
min := D [x,Near[x]] ; v := x
end;
{Можно наряду с Near[*] использовать рабочий массив расстояний Dist[x] = D [x,Near[x]] }
24.03.2014 |
Алгоритмы на графах: |
21 |
|
построение МОД |
|
b |
20 |
c |
Алгоритм Ярника-Прима-Дейкстры |
|
|
|
23 |
1 |
4 |
15 |
|
Начальная вершина – g |
|
g |
|
36 |
a 9 |
|
d |
|
|
|
|||||
26 |
25 |
16 |
3 |
|
W(T) = 23+1+4+9+3+17 = 57 |
|
|
|
|
|
|||
f e
17
a |
g |
a |
b |
a |
|
a |
|
a |
|
a |
b |
g |
b |
|
b |
|
b |
|
b |
|
b |
c |
|
c |
b |
c |
a |
c |
|
c |
|
c |
d |
|
d |
|
d |
a |
d |
a |
d |
|
d |
e |
e |
e |
a |
e |
a |
e |
d |
e |
||
f |
g |
f |
g |
f |
a |
f |
a |
f |
a |
f e |
24.03.2014 |
Алгоритмы на графах: |
22 |
|
построение МОД |
|

4. Нижняя граница задачи нахождения МОД
Худший случай: полный граф m = n(n 1)/2. Алгоритм ЯПД – асимптотически оптимальный.
Действительно, симметричная матрица весов содержит n(n1)/2 элементов. В том числе и вес минимального ребра.
Сопоставим задачу МОД с задачей нахождения минимума из n(n 1)/2 элементов, которая решается за n(n 1)/2 шагов и не менее.
Пусть для заданной матрицы решили задачу МОД.
Из остовного дерева, содержащего (n 1) ребро, за (n 1) шаг извлекаем минимальный элемент матрицы.
Если задача МОД решается за менее, чем n(n 1)/2 (n 1) шагов, то и задачу нахождения минимума из n(n 1)/2 элементов можно решить за менее, чем n(n 1)/2 шагов, что неверно.
Итак, нижняя граница задачи МОД: O(n2).
24.03.2014 |
Алгоритмы на графах: |
23 |
|
построение МОД |
|

Реализация алгоритма Ярника-Прима-Дейкстры для разреженных графов
Пусть наряду с Near[*] используется рабочий массив расстояний Dist[x] = D [x,Near[x]]. Реализуем из данных (x, Near[x], Dist[x]) очередь с приоритетами по ключу Dist[x].
Минимальный элемент извлекается (с восстановлением пирамиды) за O (log n) действий.
При помещении вершины v в остовное дерево производим коррекцию данных о вершинах, смежных с v и находящихся в очереди. Коррекция каждой такой вершины x (ребра {v, x}) требует O (log n) действий, но при этом такое ребро «возникает» и «исчезает» лишь один раз за все время. Т.о. суммарно требуется O ((n+m) log n) операций, или, что то же O (m log n).
Ср. с O (n2) (например, при m =O (n))
24.03.2014 |
Алгоритмы на графах: |
25 |
|
построение МОД |
|

Алгоритм Ярника-Прима-Дейкстры построения МОД
Примеры выполнения. Варианты:
•Стандартный - для «плотных» графов (m
=O(n))
•Для разреженных графов (m = O(n))
24.03.2014 |
Алгоритмы на графах: |
26 |
|
построение МОД |
|
Пример 1. МОД. Алгоритм ЯПД (n = 9; m = 20)
b17
16 |
3 |
|
|
|
4 |
i1
8
11 9
h7
* |
a |
0 шаг |
- |
1 шаг |
- |
2 шаг |
- |
24.03.2014 |
|
c
2
a
10
g
|
14 d |
b |
17 |
c |
14 d |
20 |
15 |
|
3 |
20 |
15 |
|
19 |
16 |
2 |
19 |
|
|
|
||||
|
|
|
4 |
|
13
5
12
6
b  c
c
4 2
4  2
2
4 !-
e |
|
i |
|
1 |
|
a |
|
|
|
|
|||||
|
18 |
8 |
|
|
10 |
||
|
|
|
11 |
9 |
|
||
|
|
|
|
|
|||
f |
h |
|
7 |
|
g |
||
|
d |
e |
f |
g |
|||
15 |
13 |
|
12 |
10 |
|||
15 |
13 |
|
12 |
9 |
|||
14 |
13 |
|
12 |
9 |
|||
13
5
12
6
h
11
8
8
e
18
f
i
1 !-
-
Алгоритмы на графах: Упрощенное представление 27 построение МОД
Пример 1. МОД.
b |
17 |
c |
14 |
||
16 |
|
3 |
20 |
15 |
|
|
2 |
|
|||
|
|
|
|||
|
|
4 |
|
||
i |
|
1 |
a |
13 |
|
8 |
|
|
10 |
5 |
|
11 |
9 |
12 |
|||
|
|
||||
h 7 g 6
Алгоритм ЯПД (n = 9; m = 20) 2
d
|
19 |
После двух шагов |
|
|
|
e |
Текущее МОД: {a, i, c} |
|
|
||
18 |
После четырех шагов |
f |
Текущее МОД: {a, i, c, b, h} |
 2 шаг
2 шаг 
 3 шаг
3 шаг 
 4 шаг
4 шаг 
a |
b |
c |
d |
e |
f |
g |
h |
i |
- |
4 |
!- |
14 |
13 |
12 |
9 |
8 |
- |
- |
!- |
- |
14 |
13 |
12 |
9 |
8 |
- |
- |
- |
- |
14 |
13 |
12 |
7 (7) |
!- |
- |
24.03.2014 |
Алгоритмы на графах: |
28 |
|
построение МОД |
|
Пример 1. МОД. Алгоритм ЯПД (n = 9; m = 20) 3
b |
17 |
c |
|
14 |
|
d |
|
|||||
|
20 15 |
После четырех шагов |
||||||||||
16 |
|
|
3 |
2 |
|
|
19 |
|||||
|
|
|
|
|
|
|
|
Текущее МОД: {a, i, c, b, h} |
||||
|
|
|
|
4 |
|
|
|
|
|
|
||
|
i |
1 |
a |
|
13 |
|
e |
|
||||
|
|
|
|
|
||||||||
|
|
|
|
|
||||||||
8 |
|
11 |
9 |
10 |
|
5 |
|
|
18 |
После шести шагов |
||
|
|
|
|
|
12 |
|
|
|
||||
h |
7 |
|
g |
|
6 |
|
f |
Текущее МОД: {a, i, c, b, h, g, e} |
||||
 4 шаг
4 шаг 
 5 шаг
5 шаг 
 6 шаг
6 шаг 
a |
b |
c |
d |
e |
f |
g |
h |
i |
- |
- |
- |
14 |
13 |
12 |
7 |
!- |
- |
- |
- |
- |
14 |
5 (5) |
6 |
!- |
- |
- |
- |
- |
- |
14 |
!- |
6 |
- |
- |
- |
24.03.2014 |
Алгоритмы на графах: |
29 |
|
построение МОД |
|
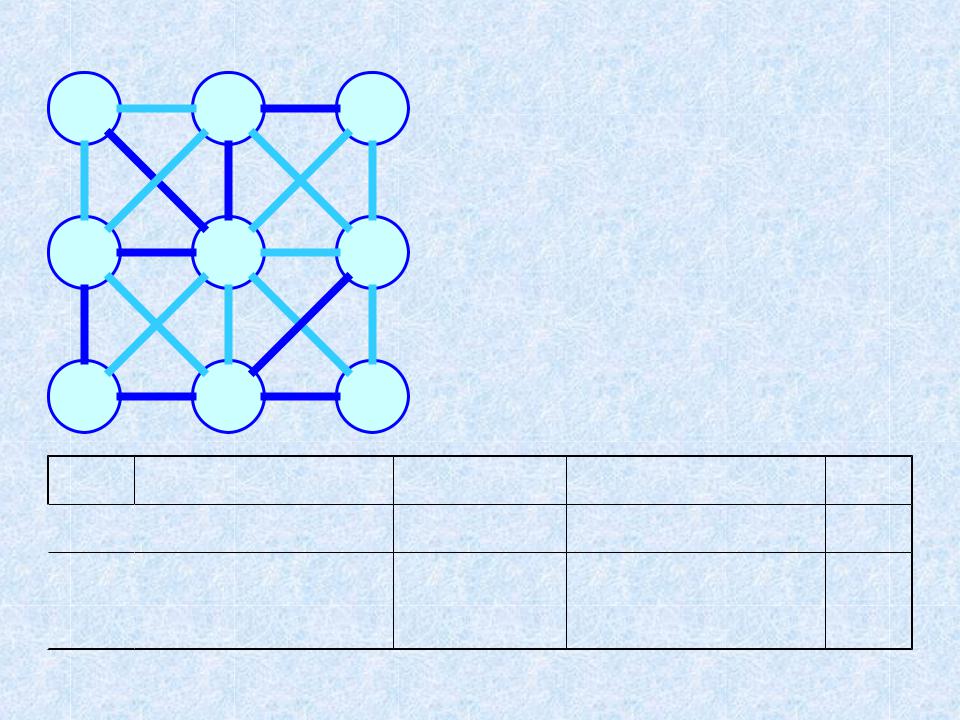
Пример 1. МОД. Алгоритм ЯПД (n = 9; m = 20) 4
b17
16 |
3 |
|
|
|
4 |
i1
8
11 9
h7
a
c
2
a
10
g
14
20 15
13
5
12
6
b c
d
19
e
18
f
После шести шагов
Текущее МОД: {a, i, c, b, h, g, e}
После восьми шагов Результат - МОД:
{a, i, c, b, h, g, e, f,
d}
W = 1+2+4+8+7+5+6+14 = 47
d |
e |
f |
g |
h |
i |
 6 шаг
6 шаг 
 7 шаг
7 шаг 
 8 шаг
8 шаг 
- |
- |
- |
14 |
!- |
6 |
- |
- |
- |
- |
- |
- |
14 |
- |
!- |
- |
- |
- |
- |
- |
- |
!- |
- |
- |
- |
- |
- |
24.03.2014 |
Алгоритмы на графах: |
30 |
|
построение МОД |
|

Пример выполнения алгоритма Ярника-Прима-Дейкстры
– вариант для разреженных графов
См. слайд 25
24.03.2014 |
Алгоритмы на графах: |
31 |
|
построение МОД |
|
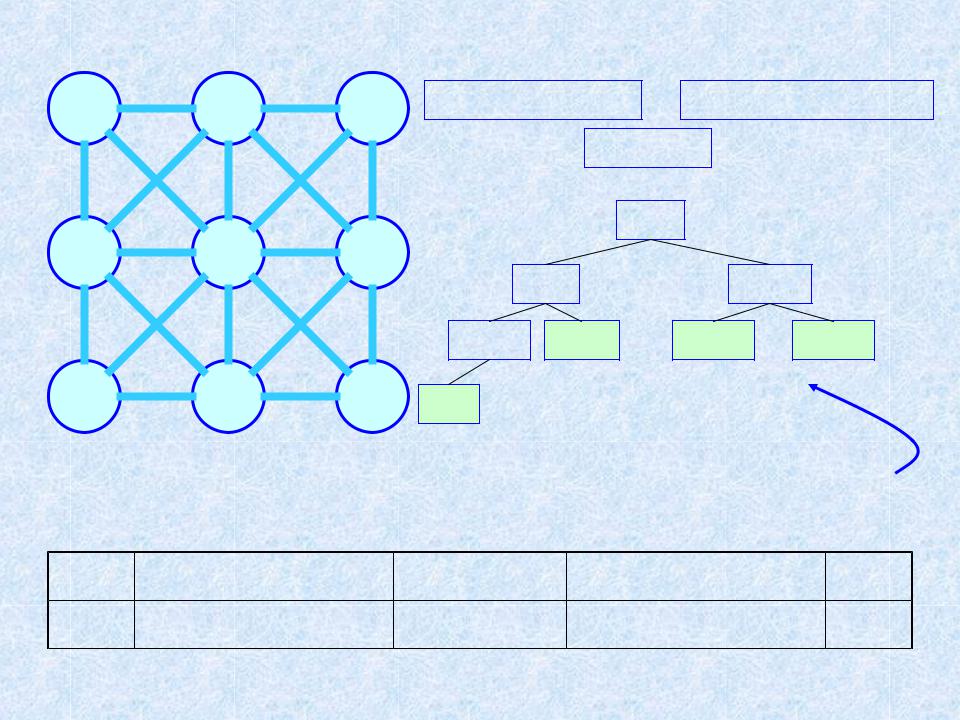
Пример 2. МОД. Алгоритм ЯПД (n = 9; m = 20) 1
b |
17 |
c |
14 |
d |
(x, Near[x], Dist[x]) |
Dist[x] = D [x,Near[x]]. |
||||
|
|
|
|
|||||||
16 |
|
3 |
20 |
15 |
19 |
|
(x, Dist[x]) |
|
||
|
2 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
||||
|
|
4 |
|
|
|
(b,4) |
|
|
||
i |
1 |
|
a |
|
e |
|
|
|
||
|
13 |
|
(c,2) |
(d,15) |
|
|||||
|
|
|
|
5 |
|
|
|
|||
8 |
|
|
10 |
18 |
|
|
|
|
||
11 |
9 |
12 |
(e,13) |
(f,12) |
(g,10) |
(h,11) |
||||
|
|
|||||||||
h |
7 |
|
g |
6 |
f |
(i,1) |
|
|
|
|
|
(b,4) |
|
(c,2) |
|
(d,15) |
(e,13) |
|
(f,12) |
|
(g,10) |
|
(h,11) |
|
(i,1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
b |
|
c |
|
d |
e |
|
f |
|
g |
|
h |
|
i |
0 шаг - |
4 |
2 |
15 |
13 |
12 |
10 |
11 |
1 |
||||||
24.03.2014 |
Алгоритмы на графах: |
32 |
|
построение МОД |
|
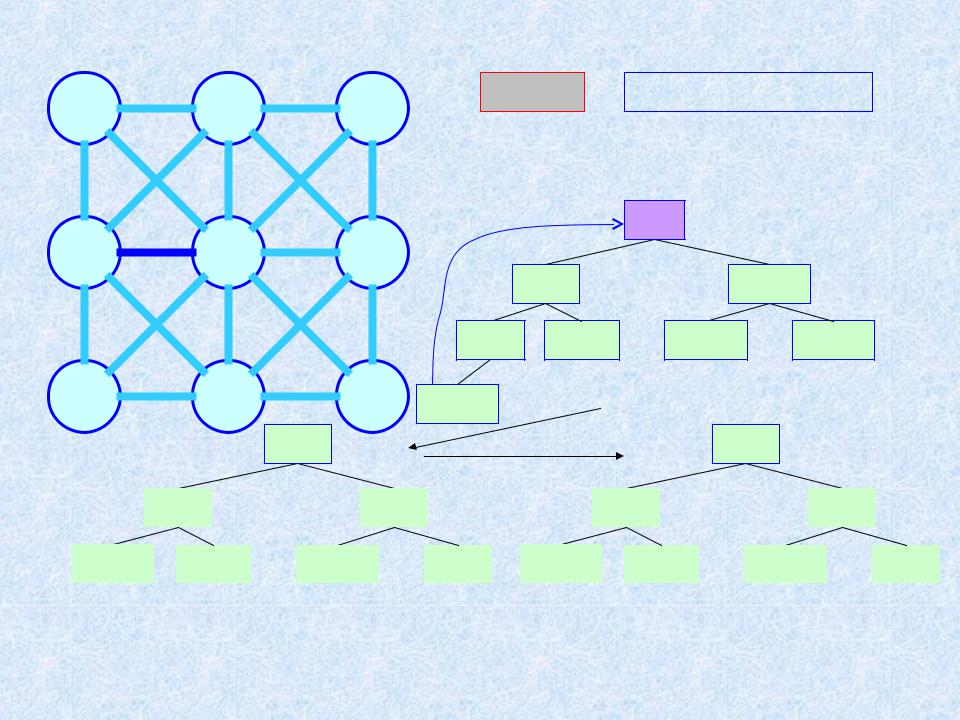
Пример 2. МОД. Алгоритм ЯПД (n = 9; m = 20) 2
b 17 c
16 |
3 |
2 |
|
||
|
4 |
i 1 a
8 10
11 9
h 7 g
14
20 15
13
5
12
6
(c,2)
d
19
e
18
f
Шаг 1 ТМОД = {a, i}
|
|
(i,1) |
|
|
(c,2) |
|
(g,10) |
(b,4) |
(f,12) |
(d,15) |
(h,11) |
(e,13)
(c,2)
|
|
(b,4) |
|
|
|
(g,9) |
|
|
|
|
|
(b,4) |
|
|
|
|
(h,8) |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(e,13) |
|
(f,12) |
|
(d,15) |
|
|
(h,8) |
|
(e,13) |
|
(f,12) |
|
(d,15) |
|
|
|
(g,9) |
||||||
24.03.2014 |
Алгоритмы на графах: |
33 |
|
построение МОД |
|
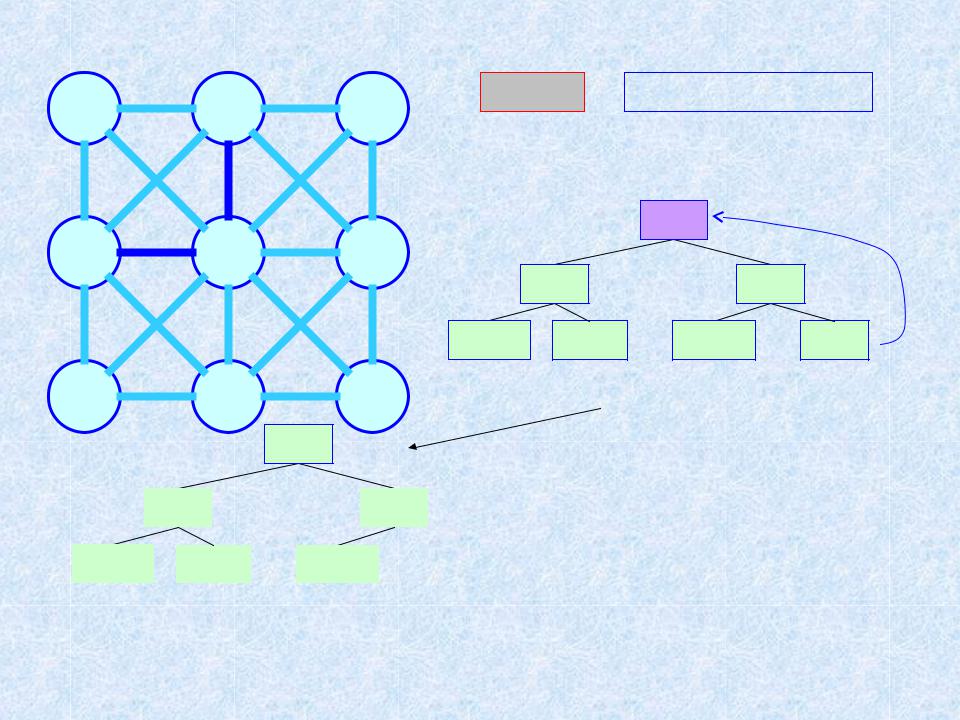
Пример 2. МОД. Алгоритм ЯПД (n = 9; m = 20) 3
b 17 c
16 |
3 |
2 |
|
||
|
4 |
i 1 a
8 10
11 9
h 7 g
14
20 15
13
5
12
6
(b,4)
d |
Шаг 2 |
ТМОД = {a, i, c} |
|
|
|
|
|
|
|
19 |
|
|
|
|
e |
|
|
(c,2) |
|
|
(b,4) |
(h,8) |
|
|
|
|
|
||
18 |
(e,13) |
(f,12) |
(d,15) |
(g,9) |
|
||||
f
|
|
(g,9) |
|
|
|
(h,8) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(e,13) |
|
(f,12) |
|
(d,14) |
|
|||
24.03.2014 |
Алгоритмы на графах: |
34 |
|
построение МОД |
|
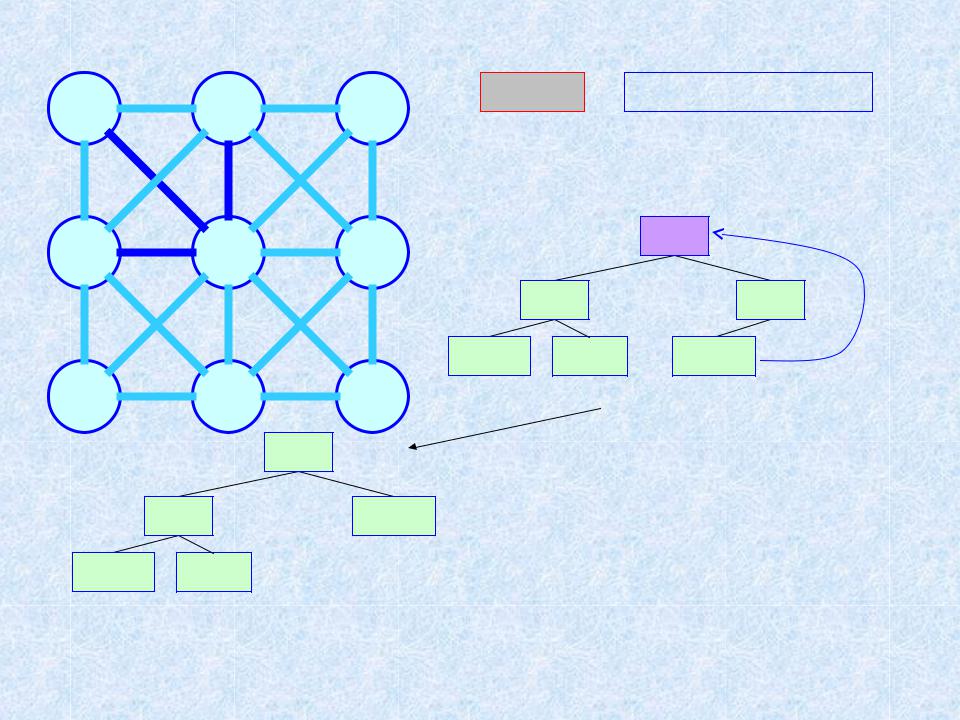
Пример 2. МОД. Алгоритм ЯПД (n = 9; m = 20) 4
b |
17 |
c |
14 |
d |
Шаг 3 |
ТМОД = {a, i, c, b} |
||
|
|
|
||||||
16 |
|
3 |
20 |
15 |
19 |
|
|
|
|
2 |
|
|
|
|
|||
|
|
|
|
|
|
|||
|
|
4 |
|
|
|
|
(b,4) |
|
i |
|
1 |
a |
13 |
e |
|
|
|
|
|
|
|
|||||
8 |
|
|
10 |
5 |
18 |
|
(g,9) |
(h,8) |
|
9 |
12 |
|
|
|
|||
11 |
|
(e,13) |
(f,12) |
(d,14) |
||||
|
|
|
|
|
|
|||
h |
7 |
g |
6 |
f |
|
|
|
|
|
|
|
(h,8) |
|
|
|
|
|
|
|
(g,9) |
|
|
(d,14) |
|
|
|
(e,13) |
|
(f,12) |
|
|
|
|
|
|
24.03.2014 |
Алгоритмы на графах: |
35 |
|
построение МОД |
|
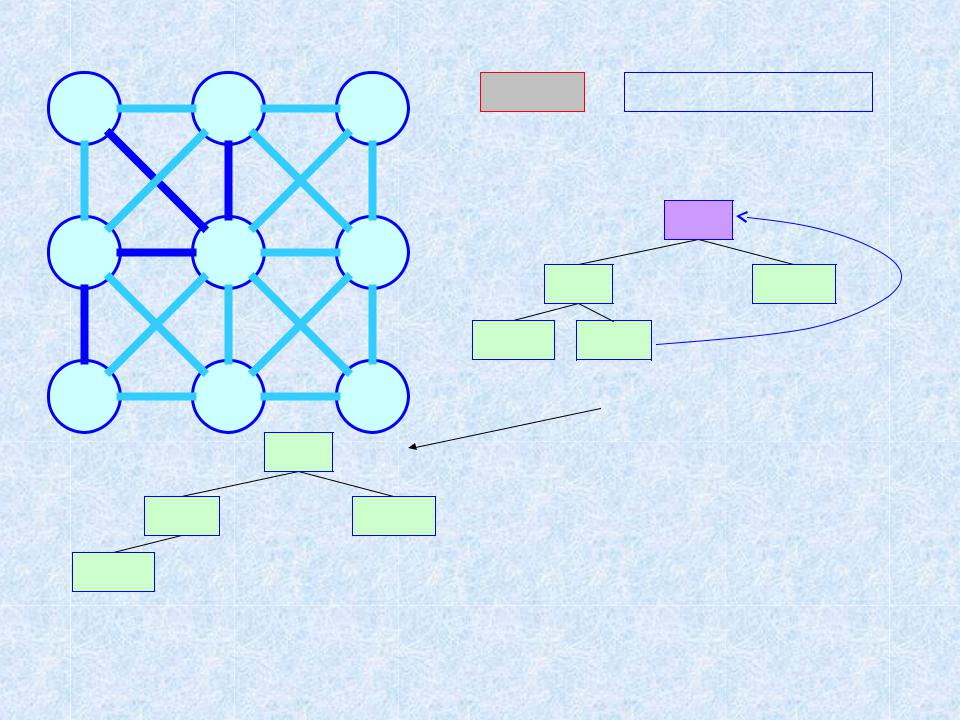
Пример 2. МОД. Алгоритм ЯПД (n = 9; m = 20) 5
b |
17 |
c |
14 |
d |
Шаг 4 |
|
ТМОД = {a, i, c, b, h} |
||
|
|
|
|||||||
16 |
|
3 |
20 |
15 |
19 |
|
|
|
|
|
2 |
|
|
|
|
||||
|
|
|
|
|
|
||||
|
|
4 |
|
|
|
|
(h,8) |
||
i |
1 |
|
a |
|
e |
|
|
||
|
13 |
|
(g,9) |
(d,14) |
|||||
|
|
|
|
5 |
|
|
|||
8 |
|
|
10 |
18 |
|
|
|
||
11 |
9 |
12 |
(e,13) |
(f,12) |
|||||
|
|
||||||||
h |
7 |
|
g |
6 |
f |
|
|
|
|
|
|
|
(g,7) |
|
|
|
|
||
(f,12) (d,14)
(e,13)
24.03.2014 |
Алгоритмы на графах: |
36 |
|
построение МОД |
|
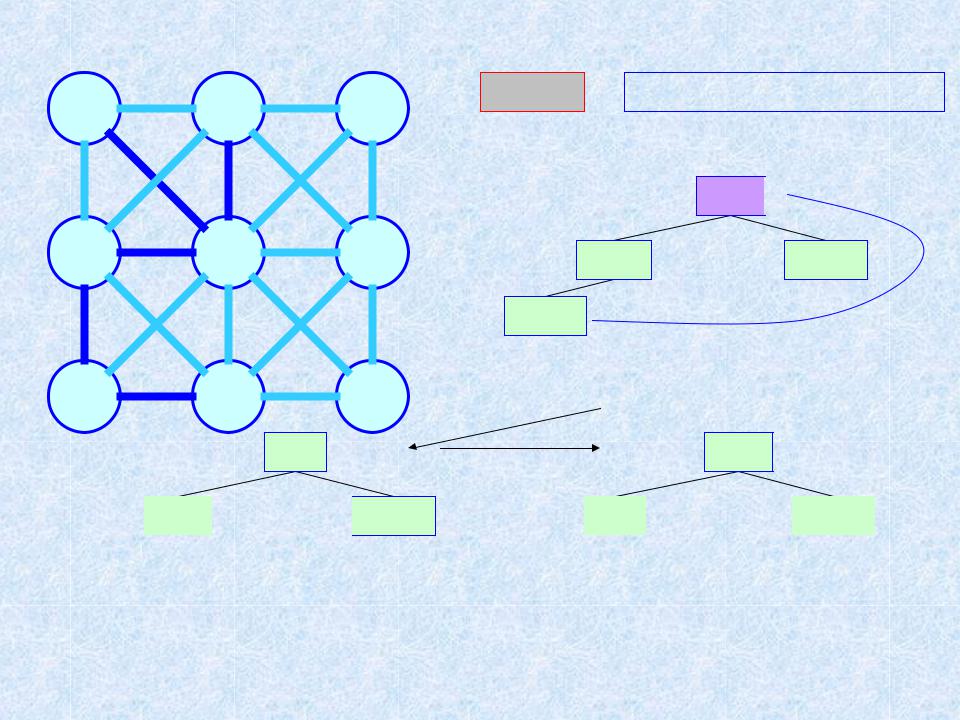
Пример 2. МОД. Алгоритм ЯПД (n = 9; m = 20) 6
b 17 c
16 |
3 |
2 |
|
||
|
4 |
i 1 a
8 10
11 9
h 7 g
14
20 15
13
5
12
6
(f,6)
d
19
e
18
f
(e,5) |
|
(d,14) |
|
|
|
Шаг 5 ТМОД = {a, i, c, b, h, g}
(g,7) 

(f,12) (d,14)
(e,13)
(e,5)
(f,6) |
|
(d,14) |
|
|
|
24.03.2014 |
Алгоритмы на графах: |
37 |
|
построение МОД |
|
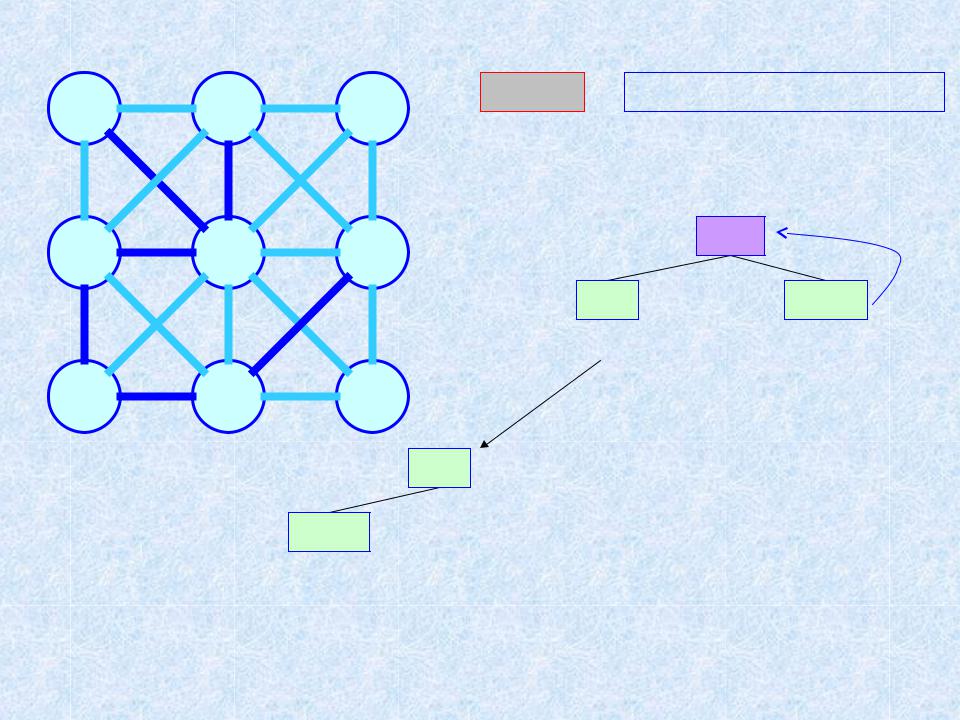
Пример 2. МОД. Алгоритм ЯПД (n = 9; m = 20) 7
b 17 c
16 |
3 |
2 |
|
||
|
4 |
i 1 a
8 10
11 9
h 7 g
|
14 |
d |
Шаг 6 |
ТМОД = {a, i, c, b, h, g, e} |
|
|
|
||
20 |
15 |
19 |
|
|
|
13 |
e |
|
(e,5) |
|
|
|
||
|
5 |
18 |
(f,6) |
(d,14) |
|
12 |
|
|
|
|
6 |
f |
|
|
(f,6)
(d,14)
24.03.2014 |
Алгоритмы на графах: |
38 |
|
построение МОД |
|
Пример 2. МОД. Алгоритм ЯПД (n = 9; m = 20) 8
b |
17 |
c |
|
14 |
|
d |
|
Шаг 7 |
|
|
|
ТМОД = {a, i, c, b, h, g, e} |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
3 |
|
20 |
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
16 |
|
|
2 |
|
19 |
|
|
|
|
|
|
|
|
|
|
(f,6) |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
i |
1 |
a |
|
13 |
|
e |
|
|
|
|
|
(d,14) |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
8 |
|
|
|
10 |
|
|
5 |
|
|
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(d,14) |
|
|
|
|
|
|||||||||
|
11 |
9 |
|
|
12 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
h |
7 |
|
g |
|
6 |
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Шаг 8 |
|
|
|
|
ТМОД = {a, i, c, b, h, g, e, f, d} |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
24.03.2014 |
Алгоритмы на графах: |
39 |
|
построение МОД |
|
