

Построение и анализ алгоритмов
Лекция 7.1 Раздел: Алгоритмы на графах
Тема лекции:
Часть 1.
Минимальное остовное дерево (МОД), как приближение в задаче коммивояжера ё
31.03.2014 |
МОД в задаче коммивояжера |
1 |

МОД, как приближение в задаче
коммивояжера
На лекции 2 рассматривались приближенные алгоритмы решения задачи коммивояжера (ЗК):
•АБС – алгоритм ближайшего соседа
•АВБГ – алгоритм включения ближайшего города
Если рассматривается евклидов (частный) случай ЗК, то существуют оценки отклонения стоимости приближенного решения от стоимости точного решения.
Евклидова ЗК: Матрица стоимостей {Cij}:
(а) симметрична (б) удовлетворяет неравенству треугольника
Cij Cik + Ckj , i, j, k
31.03.2014 |
МОД в задаче коммивояжера |
2 |

Более точная терминология
Лучше (более точно) называть это задачей коммивояжера с неравенством треугольника (ЗКНТ)
На плоскости при использовании евклидова расстояния неравенство треугольника выполняется (но есть и другие случаи с НТ)
vi pi (xi , yi ) |
|
|
|
||
|
|
|
|
|
|
C (x x |
)2 |
( y y |
)2 |
|
|
ij |
i j |
|
i j |
|
|
Если стоимости вычисляются как евклидово расстояние, то это и есть евклидова задача коммивояжера (ЕЗК).
Т.о. оценки верны в случае ЗКНТ, и в т.ч. в евклидовом случае.
31.03.2014 |
МОД в задаче коммивояжера |
3 |

Оценка степени приближения
алгоритмов АБС и АВБГ в евклидовом
случае
Nn – маршрут АБС, Nn – его длина (стоимость). In – маршрут АВБГ, In – его длина (стоимость).
On – оптимальный маршрут, On – его длина (стоимость).
|
|
Nn |
|
|
|
1 |
( log2 n 1). |
|
|
|
|
|
In |
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
On |
|
|
|
2 |
|
|
|
On |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Было ранее без доказательства!
31.03.2014 |
МОД в задаче коммивояжера |
4 |

Новое:
Приближенный алгоритм двойного обхода МОД при решении ЗК
1)Для заданного графа ЗКНТ построить МОД
2)Начиная с любой вершины обойти по ребрам МОД все вершины, «спрямляя пути» при возвратах к уже посещенным вершинам, и вернуться в стартовую вершину
Другие формулировки п.2:
2’) Сделать двойной обход МОД. В списке пройденных вершин вычеркнуть повторения (оставить первые вхождения).
2”) Обойти МОД в прямом порядке, фиксируя первые посещения вершин.
31.03.2014 |
МОД в задаче коммивояжера |
5 |
|
|
|
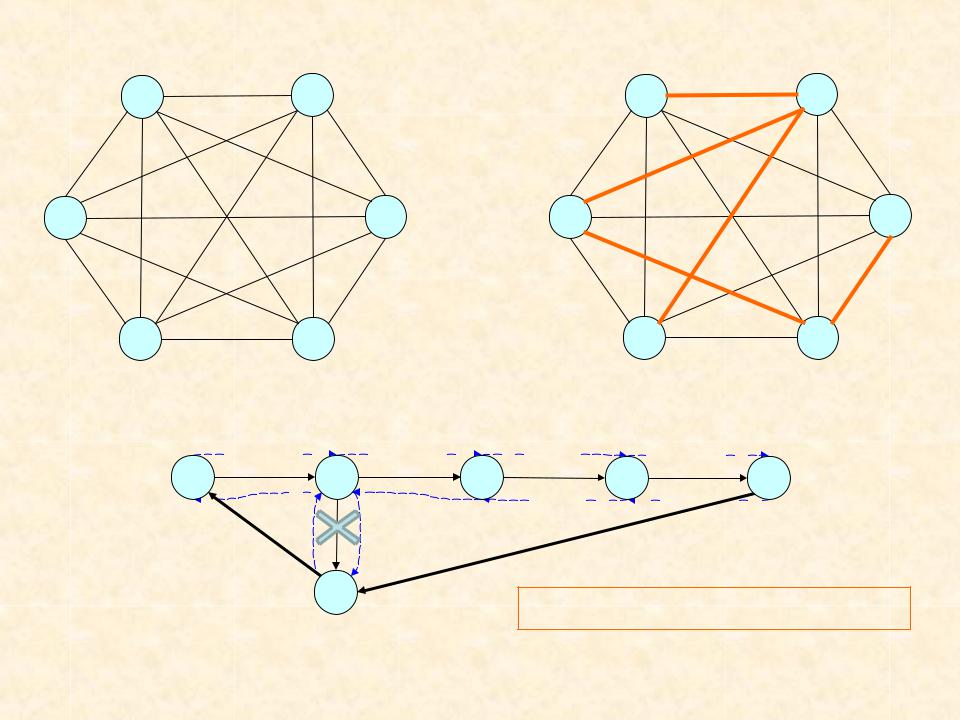
Граф |
|
Пример |
|
Граф и МОД |
|
|||
|
1 |
|
4 |
2 |
|
|
1 |
|
4 |
2 |
|
|
|
|
|
|
|
|
|
||||
10 |
5 |
6 |
|
8 |
12 |
10 |
5 |
6 |
|
8 |
12 |
|
|
2 |
10 |
|
|
|
2 |
|
10 |
||
|
|
|
|
|
|
16 |
|
||||
6 |
|
16 |
|
3 |
6 |
|
|
|
3 |
||
|
|
6 |
18 |
18 |
|
|
|
6 |
18 |
|
18 |
16 |
|
|
|
4 |
16 |
|
|
|
4 |
||
|
|
|
|
|
|
|
|
||||
|
5 |
|
14 |
4 |
|
|
5 |
|
14 |
4 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
МОД |
|
|
|
|
|
|
|
|
|
4 |
2 |
6 |
6 |
4 |
4 |
3 |
|
|
|
|
|
1 |
6 |
|
|
|
|
|||
|
|
|
5 |
|
|
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
= 4 + 6 + 6 + 4 + 18 + 5 = 43 |
|||||
|
|
|
|
|
|
||||||
31.03.2014 |
МОД в задаче коммивояжера |
6 |
|
|
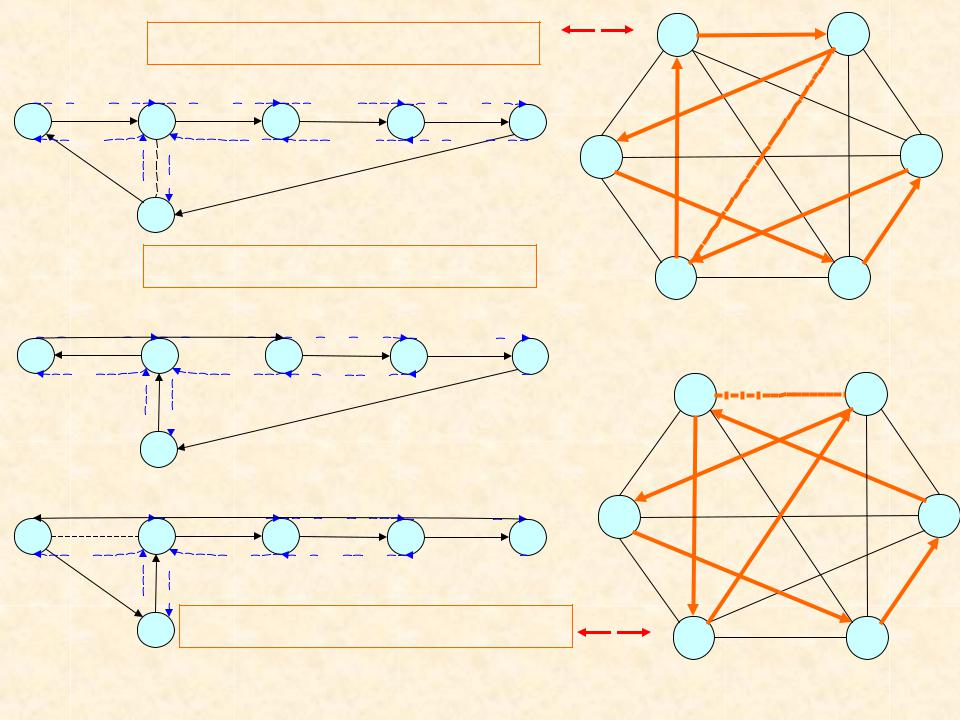
= 4 + 6 + 6 + 4 + 18 + 5 = 43 |
|
1 |
|
4 |
2 |
|
|||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
12 |
||||||
|
4 |
|
6 |
|
|
|
|
10 |
5 |
6 |
|
8 |
|
1 |
2 |
6 |
6 |
4 |
4 |
3 |
|
2 |
|
10 |
|||
|
|
2 |
|
|
|
|
|
6 |
|
16 |
|
|
3 |
|
5 |
|
|
|
18 |
|
|
|
|
18 |
|
18 |
|
|
5 |
|
|
|
|
|
|
6 |
|
||||
|
|
|
|
|
|
16 |
|
|
|
4 |
|||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
10 |
= 2 + 4 + 10 + 6 + 4 + 18 = 44 |
||||||
|
|
|
|
|
|
|
|
|
1 |
4 |
2 |
|
6 |
6 |
4 |
4 |
3 |
|
|
2 |
|
|
|
|
|
|
|
|
5 |
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
6 |
6 |
6 |
4 |
4 |
3 |
|
5 |
2 |
|
|
|
|
|
|
|
5 |
= 2 + 6 + 6 + 4 + 10 + 5 = 33 |
||||||
|
|
|||||||
|
31.03.2014 |
|
|
МОД в задаче коммивояжера |
||||
|
5 |
|
14 |
4 |
|
|
|
|
|
|
|
|
1 |
|
4 |
2 |
|
|
|
|
|
||
10 |
5 |
6 |
|
8 |
12 |
|
|
2 |
|
10 |
|
|
|
16 |
|
||
6 |
|
|
|
3 |
|
|
|
6 |
18 |
|
18 |
16 |
|
|
|
4 |
|
|
|
|
|
||
|
5 |
|
14 |
4 |
|
|
|
|
|
7 |
|
|
|
|
|
|
Оценка приближения алгоритма двойного обхода МОД (АДО МОД)
Пусть
On(стоимость);– оптимальный маршрут, On – его длина
OДn – остовное дерево, OДn – его длина (стоимость);
МOДn – минимальное остовное дерево, МOДn – его стоимость;
Мn – маршрут АДО МОД, Мn – его стоимость.
Mn 2
On
31.03.2014 |
МОД в задаче коммивояжера |
8 |

Доказательство оценки
Пусть есть оптимальный маршрут (цикл) On . Удалим одно из ребер этого цикла – получим ОДn . При этом On OДn МOДn .
В силу неравенства треугольника и смысла АДО МОД имеем 2 МOДn Мn .
Из неравенств 2 On 2 МOДn и 2 МOДn Мn следует, что 2 On Мn , т.е.
Mn 2
On
31.03.2014 |
МОД в задаче коммивояжера |
9 |
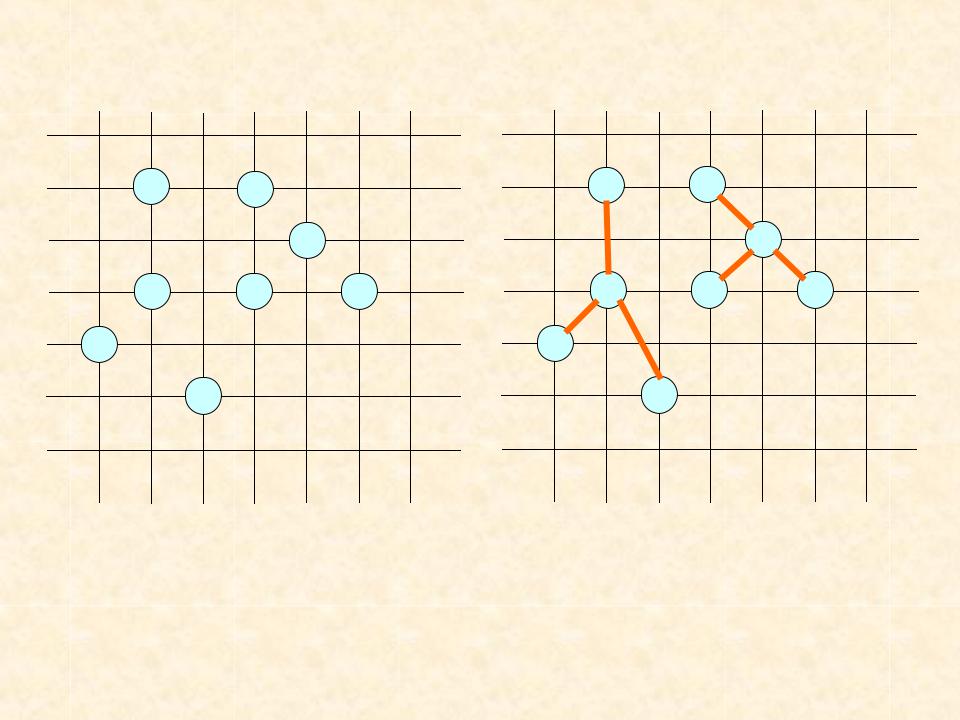
Другие примеры АДО МОД
1 4
5
2 |
6 |
7 |
3
8
Граф
(вершины)
1  4
4
5
2 |
6 |
7 |
3
8
МОД графа
31.03.2014 |
МОД в задаче коммивояжера |
10 |
