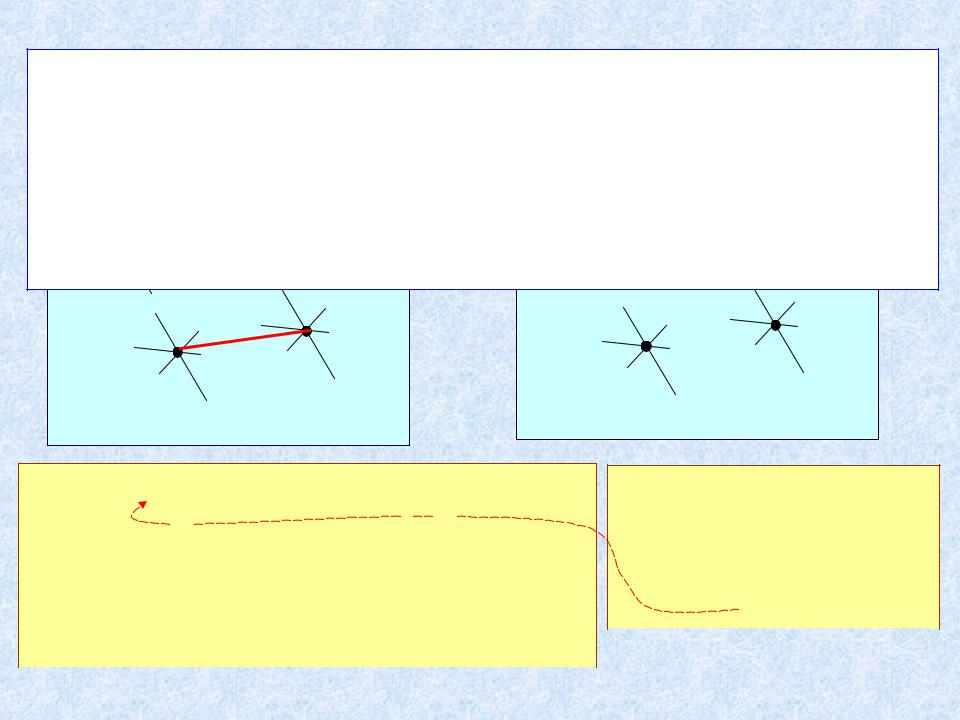
Идея алгоритма |
|
Пусть правильно построен некоторый остовный |
|
лес. |
|
Находим Кратч[i] для всех поддеревьев и |
|
добавляем их. |
|
Определяем получившиеся связные компоненты. |
|
Итерацию повторяем. |
|
W[a, b] = min {W[u, v]: u V(a), v V(a)} |
(W[b, c] < W[a, b]) & |
|
(W[c, a] < W[b, c]) |
W[b, c] = min {W[u, v]: u V(b), v V(b)} |
|
(W[c, a] < W[a, |
|
|
|
b]) !?!? |
|
||
W[c, a] = min {W[u, v]: u V(c), v V(c)} |
|
|
||
|
|
|
||
|
Это в случае, когда все веса различны |
|
||
|
|
|
|
34 |
07.04.2014 |
Поиск на графах |
|
|
|
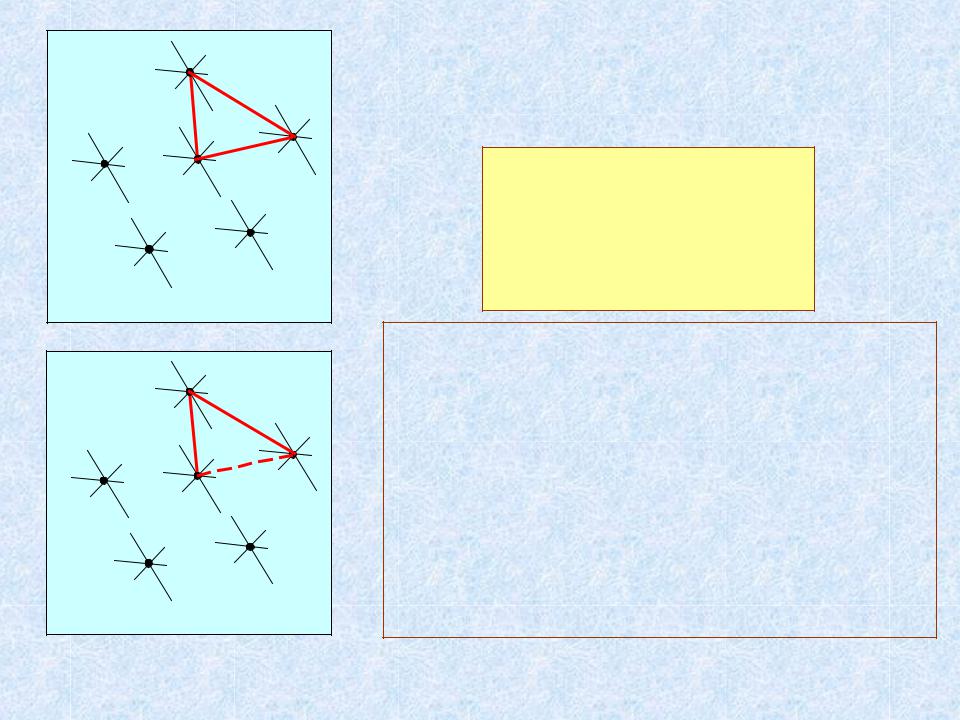
a |
b |
c |
a |
b |
c |
07.04.2014 |
Случай равных весов
(W[b, c] = W[a, b]) & (W[c, a] = W[b, c]) & (W[c, a] = W[a, b])
Цикл !?!?
Разрыв цикла
При выборе минимума в случае равных весов выбирать ребро, соединяющее с компонентой, имеющей меньший номер.
Например, a < b < c.
Тогда компонента с максимальным номером (c) не будет выбрана (при равных весах)
Поиск на графах |
35 |
{
T={ }; C={ {v1},...,{vn} }; while (Card(C)<>1) {
// этап:
for ( Si C) min[i]=+ ;
Для Si C найти Кратч[i] – кратч. из всех ребер, имеющих ровно один конец в дереве Si=(Vi,Ti) /*см. след.сл.*/
for ( Si C) T = T + { Кратч[i] } ;
Найти множество C связных компонент графа (V,T); } //while
/*Примечание: если при нахождении связных компонент вычислен массив numComp[ ] (см.сл.13-14),
то i и j, используемые далее, определяются так: i =numComp[u]; j =numComp[v] */
}
Продолжение (детализация)
for ( {u,v} E) {
пусть i и j такие, что (u Si) & (v Sj);
if (i!=j) {
if (d(u,v) < min[i]) { min[i] = d(u,v); Кратч[i] ={u,v};
};
if (d(u,v) < min[j] ) { min[j] := d(u,v); Кратч[j] := {u,v};
};
}// if (i!=j)
}// for
07.04.2014 |
Поиск на графах |
37 |
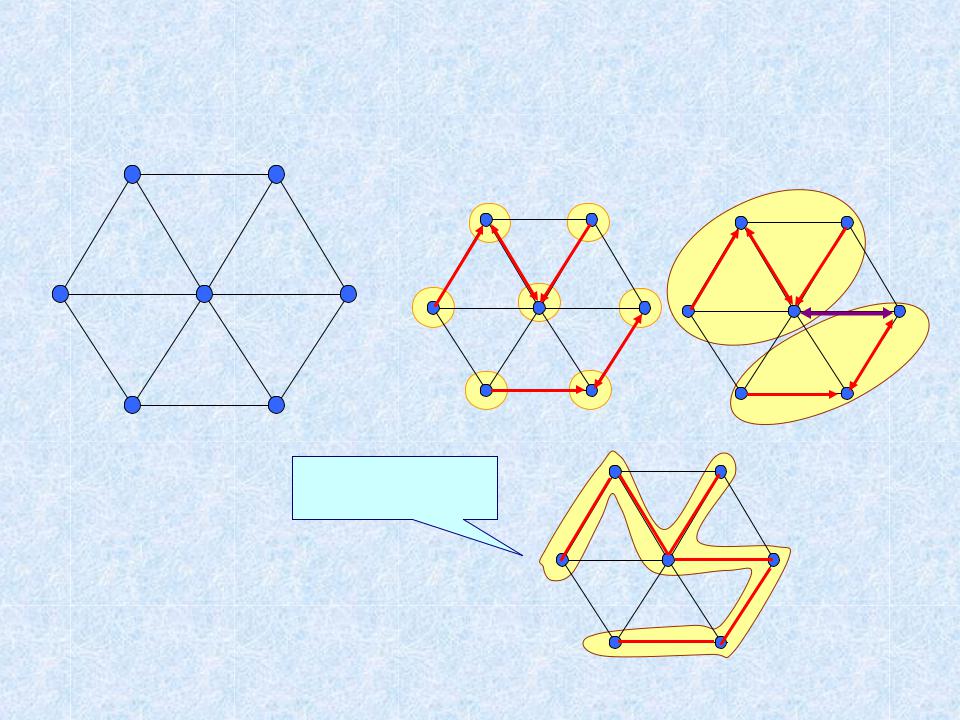
Алгоритм Борувки построения МОД
Пример
b20
23 |
1 |
4 |
c |
1 этап |
2 этап |
15
g |
|
36 |
a 9 |
d |
|
26 |
25 |
16 |
3 |
|
|
|
f e
17
Результат
07.04.2014 |
Поиск на графах |
38 |
Сложность алгоритма
На каждом новом этапе число деревьев уменьшается не менее, чем вдвое (!).
Т. о. всего не более чем log2 n этапов. Каждый этап имеет стоимость O(m). Общая сложность O(m log2 n ).
07.04.2014 |
Поиск на графах |
39 |
КОНЕЦ ЛЕКЦИИ
КОНЕЦ ЛЕКЦИИ
КОНЕЦ ЛЕКЦИИ
КОНЕЦ ЛЕКЦИИ
КОНЕЦ ЛЕКЦИИ
КОНЕЦ ЛЕКЦИИ
КОНЕЦ ЛЕКЦИИ
КОНЕЦ ЛЕКЦИИ