
- •Построение и анализ алгоритмов
- •Поиск по графу. Алгоритм пометок
- •Поиск по графу. Алгоритм пометок
- •Поиск по графу. Алгоритм пометок
- •ПОИСК В ШИРИНУ
- •ПОИСК В ШИРИНУ Пример
- •ПОИСК В ГЛУБИНУ
- •ПОИСК В ГЛУБИНУ (ПВГ)
- •Применение ПВГ
- •СВЯЗНЫЕ КОМПОНЕНТЫ (Поиск в глубину)
- •СВЯЗНЫЕ КОМПОНЕНТЫ (Поиск в глубину)
- •Пример (нахождение связных компонент)
- •Сравнение с динамическим алгоритмом нахождения связных компонент
- •Построение остовного дерева и множества обратных ребер при поиске в глубину
- •продолжение
- •Продолжение
- •Построение «глубинного» остовного дерева пример
- •Свойство DFS-остова (глубинного остовного
- •Свойство TDFS-остова (глубинного остовного дерева)
- •Замечания
- •Другая формулировка свойства DFS
- •Свойство DFS-остова
- •Построение остовного дерева
- •Построение остовного дерева
- •Замечание про прямую, обратную и противоположную теоремы (свойство ПВГ-дерева)
- •Алгоритм Борувки построения МОД O(m*log n)
- •Идея алгоритма
- •Продолжение (детализация)
- •Алгоритм Борувки построения МОД
- •Сложность алгоритма
- •КОНЕЦ ЛЕКЦИИ

Построение и анализ алгоритмов
Лекция 8 Раздел: Алгоритмы на графах
Тема лекции: Поиск по графу
07.04.2014 |
Поиск на графах |
1 |
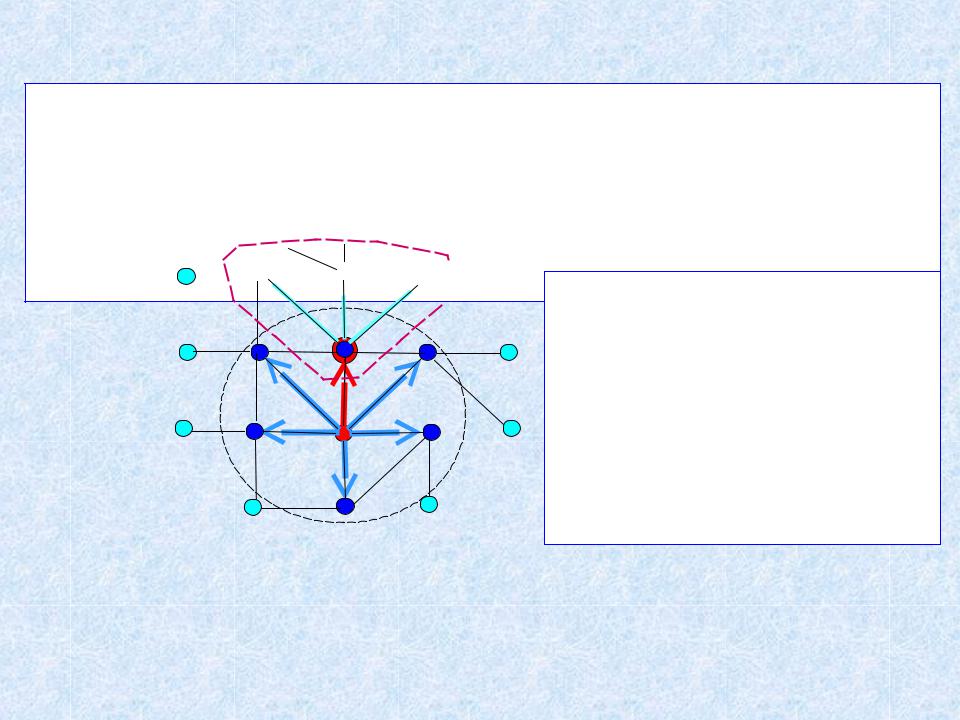
Поиск по графу. Алгоритм пометок
Обход графа: (ср.обходы дерева, леса)
•из текущей вершины (на рисунке - красная) доступны смежные (на рисунке - синие) и ещё не помеченные;
•они помечаются и заносятся в специальное
множество;


 • из множества
• из множества
извлекается очередная
вершина, она посещается (обрабатывается), и процесс повторяется, пока множество не
станет пустым.
07.04.2014 |
Поиск на графах |
2 |
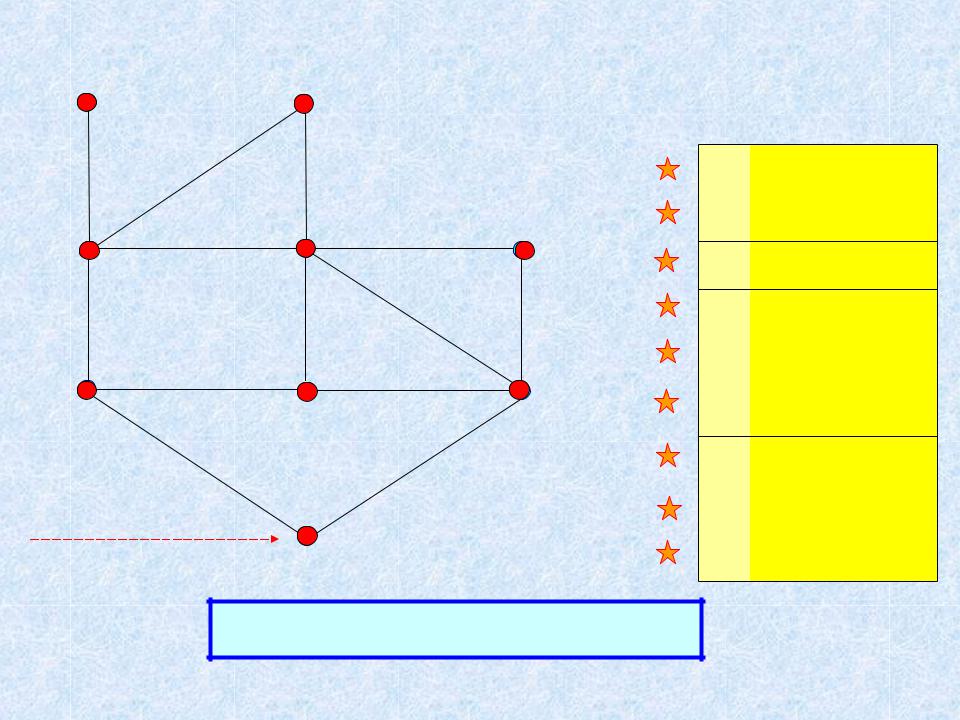
Поиск по графу. Алгоритм пометок
8 |
9 |
Структура смежности: |
||
|
|
|||
|
|
1 |
2, 4 |
|
5 |
|
2 |
1, 3, 5 |
|
7 |
3 |
2, 4, 6 |
||
|
6 |
4 |
1, 3, 6, 7 |
|
|
|
|||
2 |
4 |
5 |
2, 6, 8, 9 |
|
6 |
3, 4, 5, 7, 9 |
|||
|
3 |
|||
|
7 |
4, 6 |
||
|
|
|||
|
|
8 |
5 |
|
|
1 |
9 |
5, 6 |
|
|
|
|
||
Множеств |
|
Обход закончен! |
||
о: |
|
|
|
|
07.04.2014 |
Поиск на графах |
3 |

Поиск по графу. Алгоритм пометок
search (vert v0)
{setVert Q; // рабочее множество вершин графа bool newVert [n];
global |
setVert V; //множество вершин графа G=(V,E), Card(V)=n |
|||
listVert adj [n]; //списки смежности |
|
|||
for ( v V) newVert[v] = true; //пометить вершины как |
||||
необследованные |
|
|||
Q = { v0 }; NewVert[v0] = false; |
|
|||
while (Q { }) |
{ |
|
||
v = произвольный элемент из Q; |
|
|||
удалить v из Q; |
|
|
||
|
O(n + m) |
|||
посетить ( v ); |
|
|||
for ( u Adj[v]) { |
• каждая |
|||
if (NewVert[u]) { |
|
вершина один |
||
Q = Q + {u}; |
|
раз заносится в |
||
NewVert[u] = false; |
множество и |
|||
} // if |
|
|
один раз |
|
}//for |
|
|
исключается |
|
// вершина v - использована |
||||
•Каждое ребро |
||||
} //while |
|
|
||
} //search |
|
|
при анализе |
|
07.04.2014 |
|
Поиск на графах |
пометки |
|
|
|
|
проверяется |
|

ПОИСК В ШИРИНУ
(Breadth First Search - BFS )
•Множество Q реализуется очередью q (раньше посетили - раньше использовали).
•Заодно строится остовное дерево (T – множество
древесных ребер)
search_BFS (vert v0)
{queueVert q; bool newVert [n];
global setVert V; //множество вершин графа G=(V,E),
Card(V)=n
listVert adj [n]; //списки смежности
setBr T; // множество ветвей (branch) дерева
07.04.2014 |
Поиск на графах |
6 |

ПОИСК В ШИРИНУ ( O(n+m) )
for ( v V) newVert[v]=true;//пометить вершины как необследованные Create(q);
q v0; newVert[v0] =false; T = { };
while ( !Null( q )) { v q;
посетить ( v ); for ( u Adj[v] ) { if (newVert[u] ) { q u;
newVert[u] =false; T = T + { <v,u> };
//predVert[u] = v
}//if
}//for вершина v - использована
}//while
}// searchBFS
07.04.2014 |
Поиск на графах |
7 |
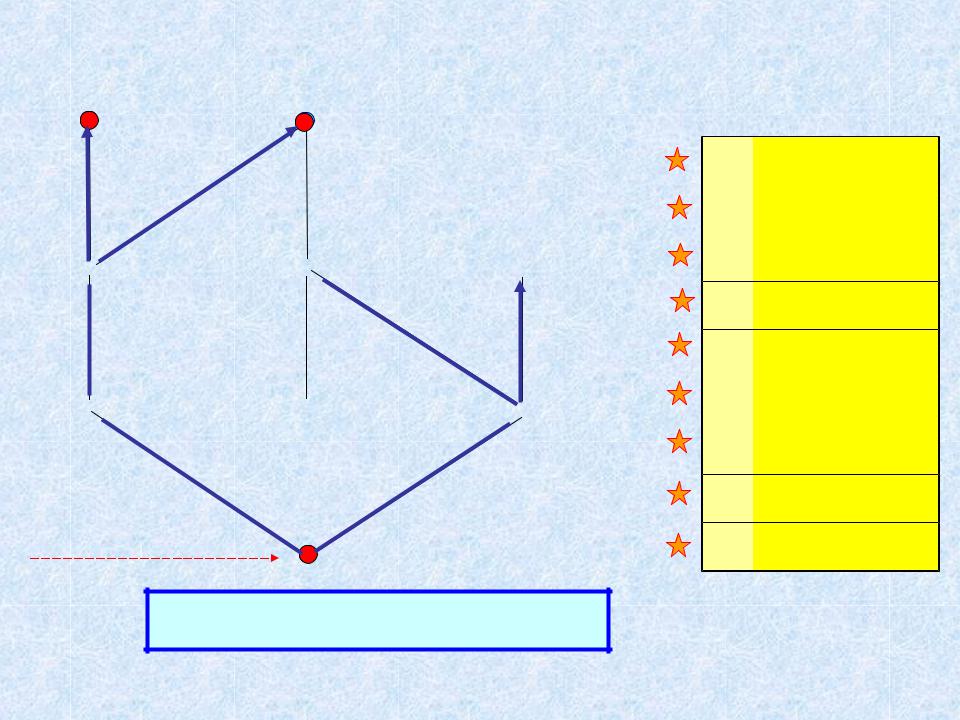
ПОИСК В ШИРИНУ Пример
8 8 |
9 9 |
5 5 

 7 7 6 6
7 7 6 6
2 2 



 4 3
4 3
3 4
|
1 |
2 |
4 |
1 |
1 |
5 |
6 |
7 8 9 |
Очередь: |
3 |
|||||||
1 |
2, 4 |
2 |
1, 3, 5 |
3 |
2, 4, 6 |
4 |
1, 3, 6, 7 |
5 |
2, 6, 8, 9 |
6 |
3, 4, 5, 7, 9 |
7 |
4, 6 |
8 |
5 |
9 |
5, 6 |
Обход закончен!
07.04.2014 |
Поиск на графах |
9 |
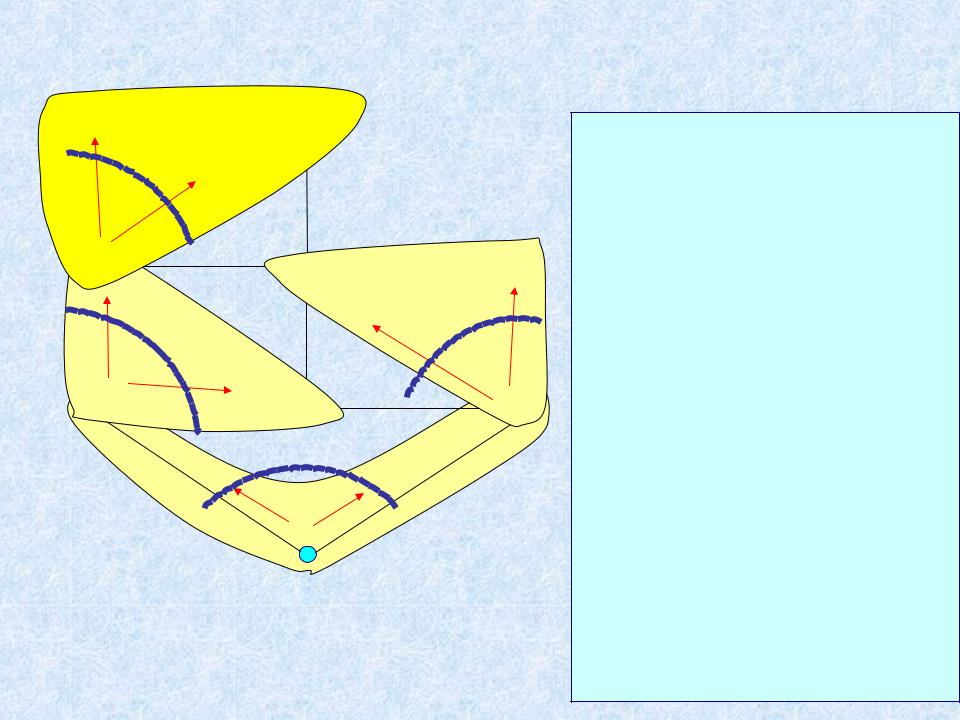
ПОИСК В ШИРИНУ = Волновой алгоритм
|
Свойство BFS-остова: |
|
|
G = (V, E) и |
|
|
(V, T) – BFS-остов |
|
|
графа G. |
|
|
Тогда путь в (V, T) из |
|
2 |
v V до корня остова |
|
4 r является |
||
3 |
||
кратчайшим путем |
||
|
из v в r в графе G. |
|
1 |
Док-во по индукции |
|
(по этапам волны |
||
|
или по порциям |
|
07.04.2014 |
Поиск на графах записи в очередь). |

ПОИСК В ГЛУБИНУ
( Depth First Search - DFS )
Q = Stack. Можно сразу рекурсивно.
searchDFS (vert v)
{ global bool newVert [n];
setVert V; //множество вершин графа G=(V,E), Card(V)=n listVert adj [n]; //списки смежности
setBr T; // множество ветвей (branch) дерева
посетить v; newVert[v] =false; for ( u Adj[v] )
if (newVert[u]) searchDFS(u);
//v - использована
} // searchDFS
07.04.2014 |
Поиск на графах |
11 |

ПОИСК В ГЛУБИНУ (ПВГ)
(Depth First Search - DFS )
//cобственно поиск в глубину в графе G=(V,E) {…
setVert V; //множество вершин графа G=(V,E), Card(V)=n
listVert adj [n]; //списки смежности for ( v V) newVert[v] = true;
// - пометить все вершины как необследованные for ( v V)
if (newVert[v] ) searchDFS(v);
}
07.04.2014 |
Поиск на графах |
12 |
|
ПОИСК В ГЛУБИНУ |
|
8 |
9 |
пример |
|
||
5 



 7 6
7 6
2 



 4 3
4 3
1
1 |
2, 4 |
2 |
1, 3, 5 |
3 |
2, 4, 6 |
4 |
1, 3, 6, 7 |
5 |
2, 6, 8, 9 |
6 |
3, 4, 5, 7, 9 |
7 |
4, 6 |
8 |
5 |
9 |
5, 6 |
07.04.2014 |
Поиск на графах |
13 |
