2.2 Приклад 2.

Вирішимо симплекс-методом з алгебраїчними перетвореннями таку задачу:

Знайти максимум функції F=x1+2x2 при обмеженнях, що -x1+2x2≥2, x1+x2≥4, x1-x2≤2, x2≤6, x1≥0 та x2≤0.

Крок I. Вводимо додаткові невід'ємні змінні x3,x4,x5,x6 та зводимо цю систему нерівностей до еквівалентної їй системи рівнянь

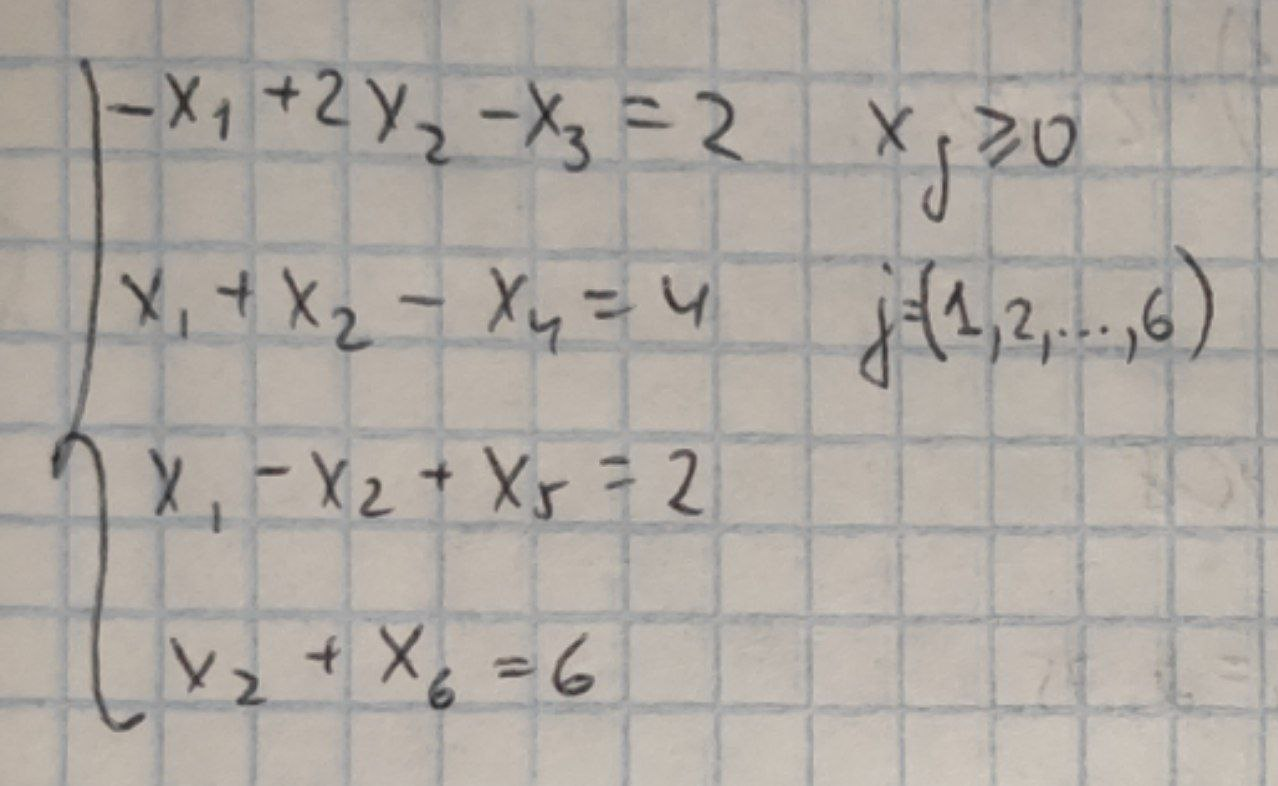
Введені додаткові змінні приймаємо за основні, тому що в цьому випадку базове рішення системи легко перебуває. Тоді x1 і x2– неосновні змінні.

Виразивши основні змінні через неосновні, отримаємо

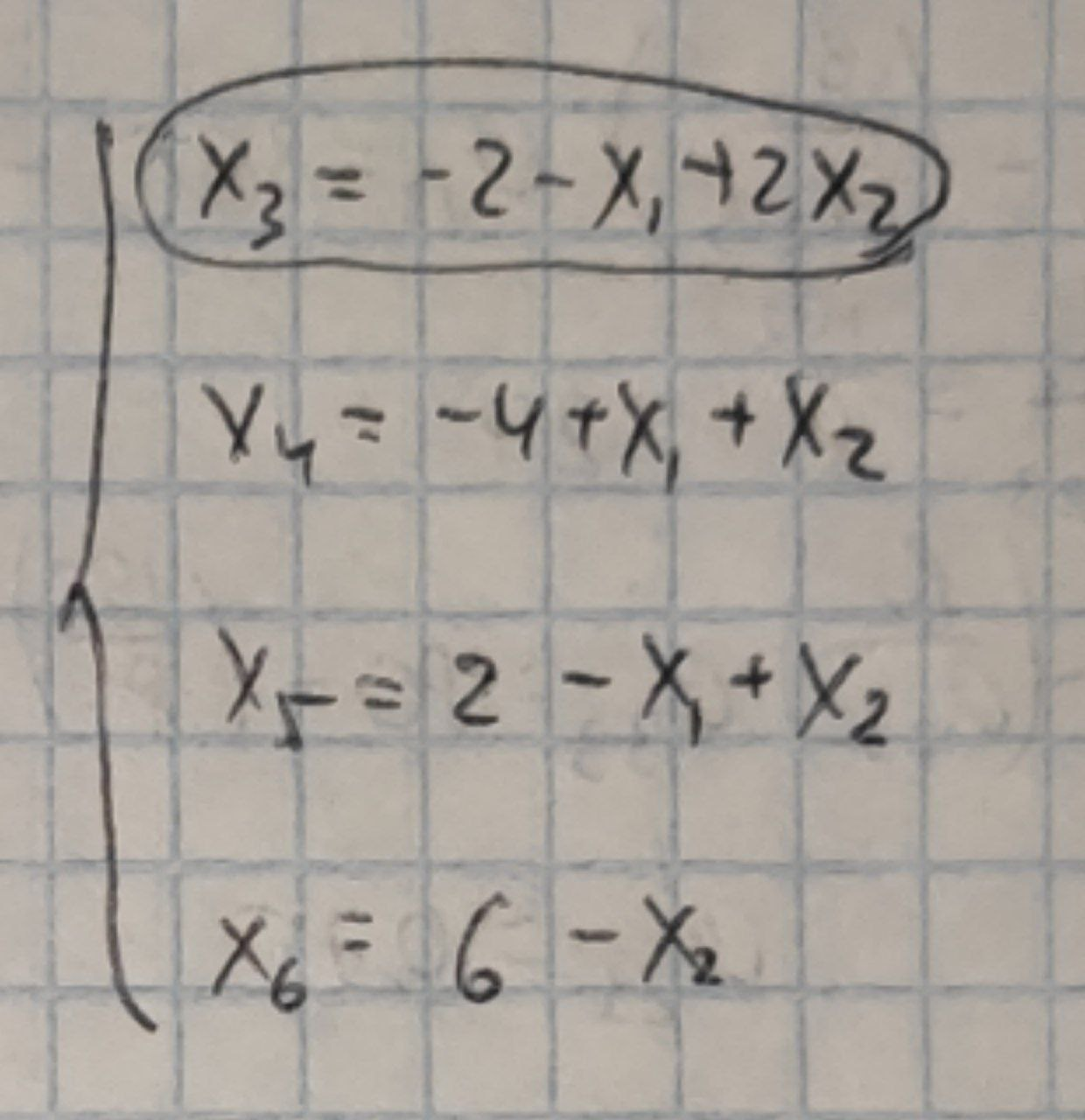
Отже, даному розбиття змінних на основні та неосновні відповідає базисне рішення (0,0,-2,-4,2,6) , яке є неприпустимим (дві змінні негативні), а тому воно не є оптимальним. Від цього базового рішення перейдемо до покращеного.

Щоб вирішити, яку змінну слід перевести з неосновних до основних, розглянемо будь-яке з двох наявних рівнянь останньої системи з негативними вільними членами, наприклад, друге. Воно показує, що в основні змінні можна перекласти x1 і x2 , тому що в цьому рівнянні вони мають позитивні коефіцієнти (отже, при їх збільшенні, а це станеться, якщо переведемо будь-яку з них до основних змінних, змінна x4 збільшиться).

Спробуємо перевести в головну змінну x1 . Щоб встановити, яку змінну слід перевести з основних у неосновні, знайдемо абсолютну величину найменшого відношення вільних членів системи до коефіцієнтів при x1. Маємо x1=min(inf, 4/1, 2/1, inf)=2 . Воно отримано з третього рівняння, що показує, що на неосновні треба перекласти змінну x5, що у вихідному базисному рішенні позитивна. Отже, отримане базове рішення, як і вихідне, містить дві негативні компоненти, тобто при переході до такого базисного рішення поліпшення не відбудеться.

Якщо ж перевести в основні змінну x2, то найменше відношення вільних членів до коефіцієнтів при x2 складе x2=min(2/2,4/1, inf, 6/1)=1. Воно отримано з першого рівняння, в якому вільний член негативний. Отже, переводячи у основні, а неосновні змінні, ми отримаємо базисне рішення, у якому число негативних компонентів на одиницю менше, ніж у вихідному. Тому зупинимося на цій можливості: переводимо x2 до основних, а x3 до неосновних змінних. Тому у наведеній вище системі рівнянь виділеним виявилося перше рівняння.

Крок ІІ. Основні змінні x2,x4,x5,x6, неосновні змінніx1,x3 .

Виразимо нові основні змінні через нові неосновні, починаючи з виділеного на кроці I рівняння. В результаті отримаємо

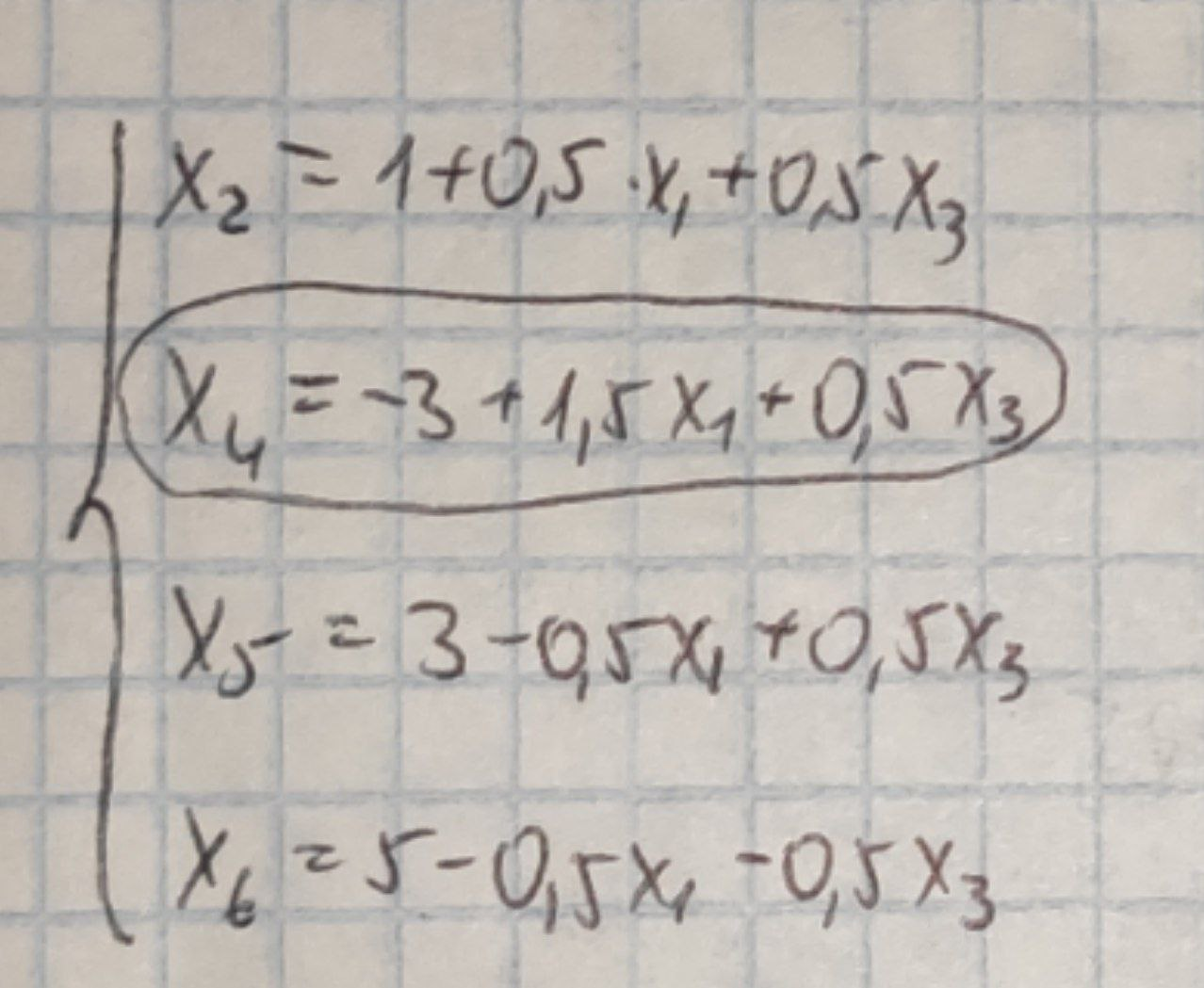
Отже, маємо нове базисне рішення (0,1,0,-3,3,5), яке також є неприпустимим, а тому оптимальним. Але в ньому, як ми й передбачали, лише одна змінна негативна (зокрема x4).

Від отриманого базового рішення необхідно перейти до іншого. Розглянемо рівняння з негативним вільним членом, тобто друге рівняння. Воно показує, що основні перемінні можна перевести x1 і x3. Переведемо в основні змінні x1. Знайдемо найменше з абсолютних величин відносин вільних членів системи до коефіцієнтів при x1. Маємо x1=min(inf, 3/1,5 ,3/0,5 ,5/0,5)=2. Значить, у неосновні змінні треба перенести x4. Оскільки найменше ставлення отримано з другого рівняння, його виділяємо. У новому базисному рішенні не виявиться негативних компонент, т. е. воно є допустимим.

В особливих випадках рішення завершується на II кроці: це, наприклад, випадки, коли максимум цільової функції – нескінченність і коли система не має жодного рішення .

Крок ІІІ. Основні змінні:x1,x2,x5,x6 , неосновні змінні: x3,x4. Виразивши основні змінні через неосновні, отримаємо

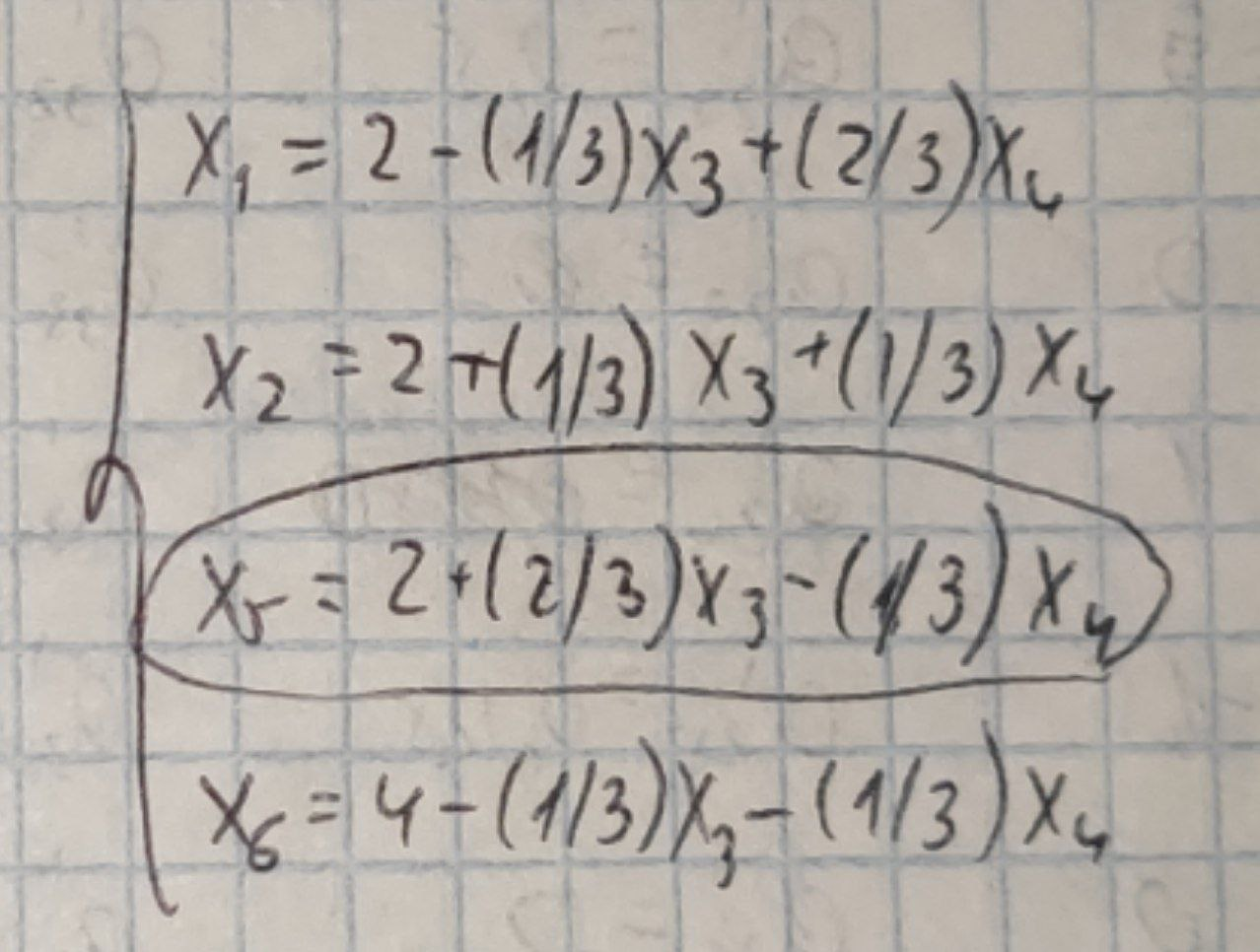
Нове базисне рішення має вигляд (2,2,0,0,2,4). Чи є воно оптимальним, можна встановити, якщо висловити лінійну форму через неосновні змінні аналізованого базисного рішення. Зробивши це, отримаємо F=6+(1/3)x3+(4/3)x4. Оскільки ми шукаємо максимум лінійної форми, а знайшли лише одне допустиме рішення, то продовжимо перебір.

Переводимо до основних змінну x4, що має більший позитивний коефіцієнт. Знаходимо x4=min(inf,inf,2/(1/3),4/(1/3))=6. Це найменше відношення отримано із третього рівняння системи, тому його виділяємо. Воно показує, що за x4=6 змінна x5=0 і тому перейде до числа неосновних.

У певному випадку рішення завершується на III кроці: це випадок, коли оптимальне рішення - не єдине .

Крок ІV. Основні змінні: x1,x2,x4,x6, неосновні змінні: x3,x5. Виразивши основні змінні через неосновні, отримаємо

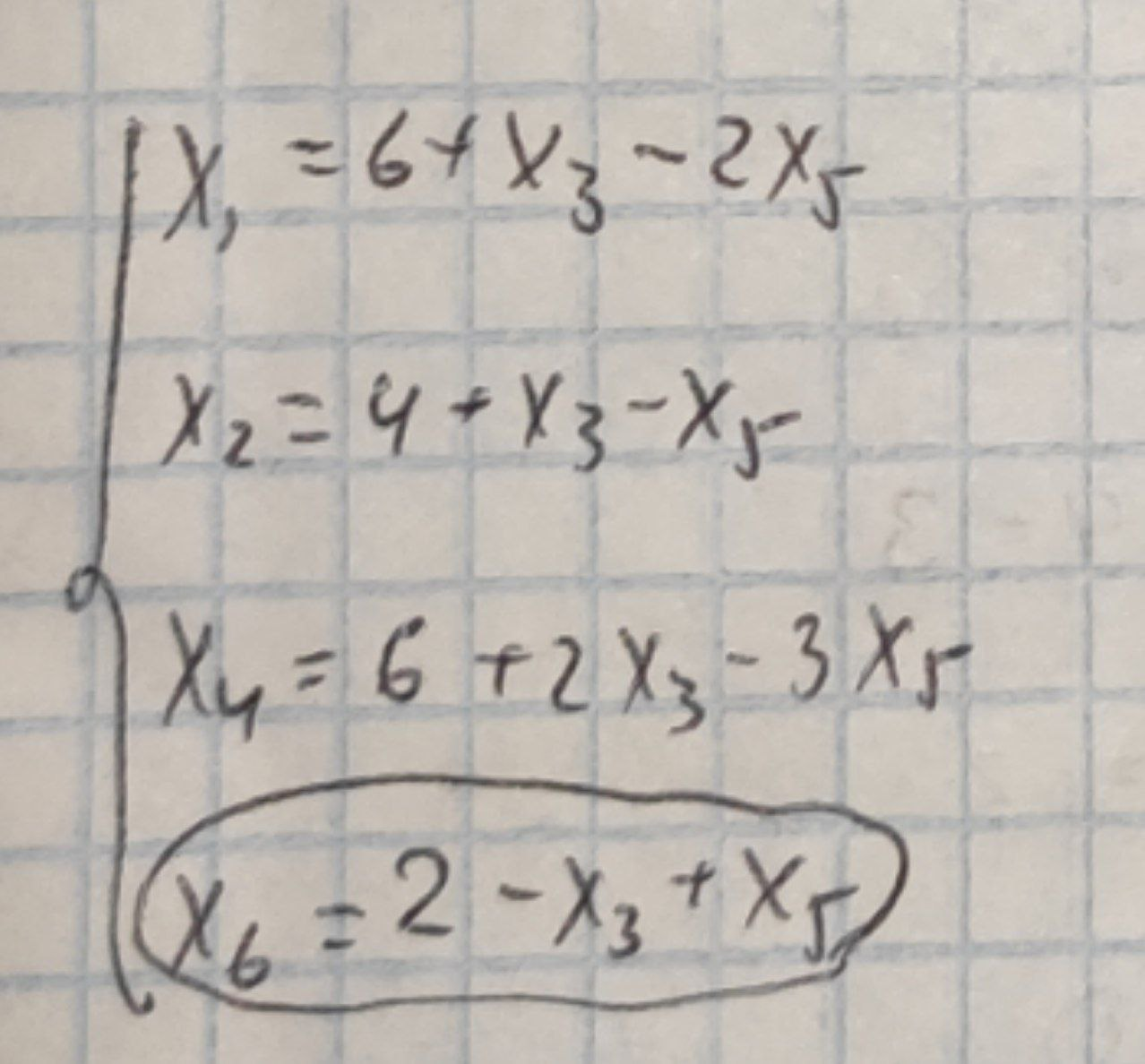
Лінійна форма, виражена через ті ж неосновні змінні, набуде вигляду F=14+3x3-4x4. Продовжимо перебір для пошуку максимуму.

Збільшення лінійної форми можливе під час початку новому базисному рішенню, у якому змінна x3 є основний. Знаходимо x3=min(inf,inf,inf,2/1)=2. Це найменше відношення отримано з четвертого рівняння системи і показує, що за x3=2 змінна x6=0 і переходить до числа неосновних.

Крок V. Основні змінні: x1,x2,x3,x4, неосновні змінні: x5,x6. Виразивши основні змінні через неосновні, отримаємо

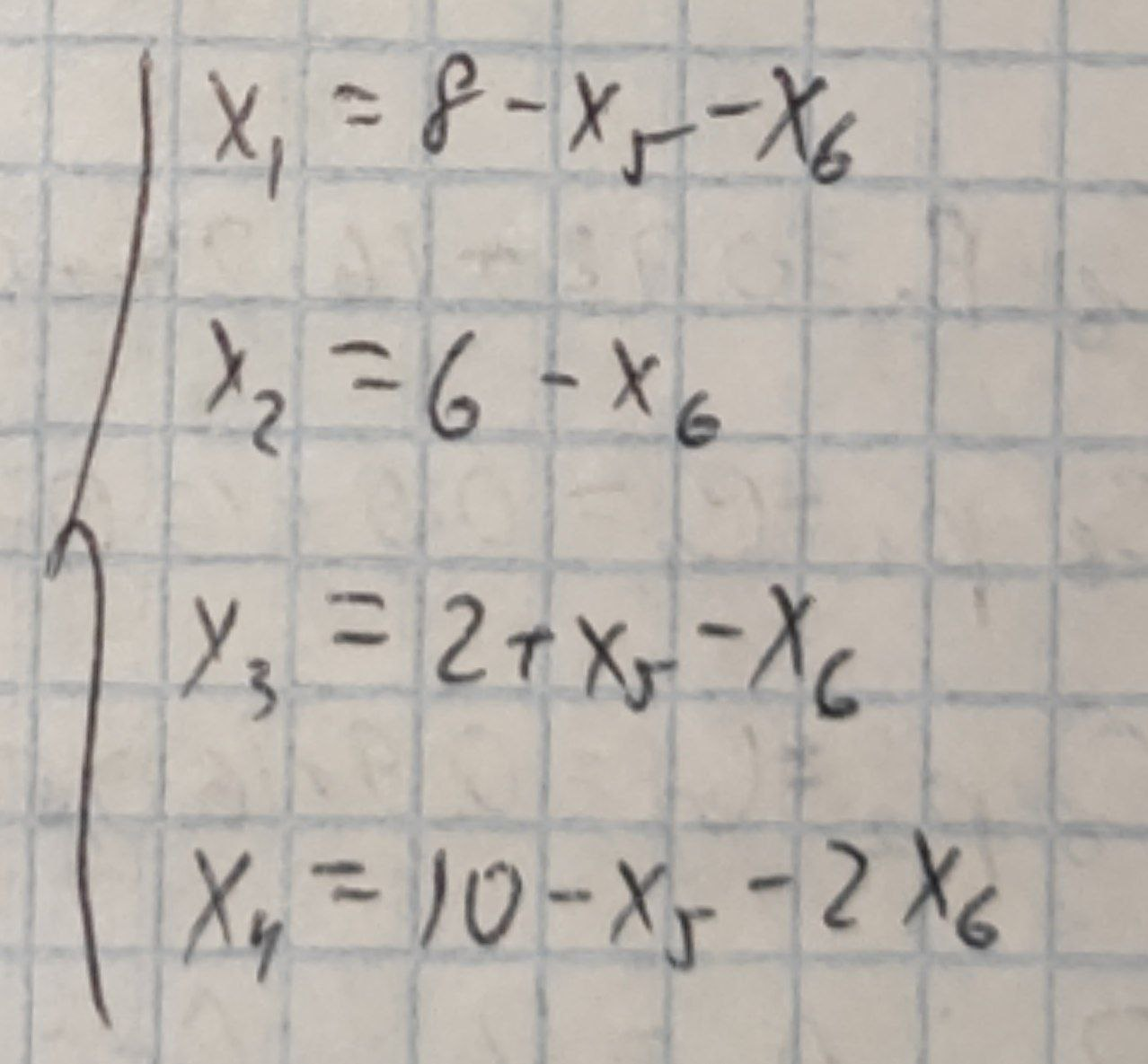
Лінійна форма, виражена через неосновні змінні нового базисного рішення, має вигляд F=20-x5-3x6. Критерій оптимальності для максимізації лінійної форми виконаний. Отже, базисне рішення (8,6,2,10,0,0) є оптимальним, а максимум лінійної форми Fmax=20