1.3 Алгоритм симплекс-метода.

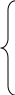Пусть система приведена до канонічного вигляду.

X1+ q1,m+1 Xm+1 + …. + q1,m+n Xm+n = H2

X2+q1,m+1 Xm+1 + …. + q1,m+n Xm+n = H2

X3+q1,m+1 Xm+1 + …. + q1,m+n Xm+n = H2

………………………………………………………

Xm+ qm,m+1 Xm+1 + …. + qm,m+n Xm+n =hm

У ній m базових змінних, k вільних змінних. m+k=n - всього змінних.

Fmin= C1X1+ C2X2+ C3X3+....+ CnXn

Для подальших міркувань обчислень користуватимемося першою симплекс таблицею (Таблиця 2):

Таблиця 2

C	B	H	C1	C2	…	Cm	Cm+1	…	Cm+k
			X1	X2	…	Xm	Xm+1	…	Xm+k
C1	X1	H2	1	0	…	0	q1,m+1	…	q1,m+k
C2	X2	H3	0	1	…	0	q2,m+1	…	q2,m+k
C3	X3	H4	0	0	…	0	q3,m+1	…	q3,m+k
…	…	…	…	…	…	…	…	…	...
…	…	…	…	…	…	…	…	…	…
Cm	Xm	Hm	0	0	…	0	qm,m+1	…	qm,m+k
		F0	F1	F2	…	Cm	Cm+1	…	Cm+k

Перший стовпець - коефіцієнти цільової функції при базисних змінних.

Другий стовпець – базисні змінні.

Третій стовпець – вільні члени (hi00).

Найвищий рядок - коефіцієнти при цільовій функції.

Другий верхній рядок - самі змінні, що входять до цільової функції та системи обмежень.

Основне поле симплекс методу – система коефіцієнтів із рівняння.

Останній рядок – служить для того, щоб відповісти на запитання: «оптимальний план чи ні».

Індексний рядок дозволяє нам судити про оптимальність плану:

При знайденні Fmin в індексному рядку повинні бути негативні та нульові оцінки.

При знайденні Fmax в індексному рядку мають бути нульові та позитивні оцінки.

Перехід до другої ітерації:

Для цього знаходимо ключовий (головний) стовпець і ключовий (головний) рядок.

Ключовим стовпцем є той, в якому знаходиться найбільший позитивний елемент індексного рядка при знайденні Fmin або найменший негативний елемент при знайденні Fmax.

Ключовим рядком називається той, у якому міститься найменше позитивне відокремлення елементів стовпця H на відповідні елементи ключового стовпця.

На перетині рядка і стовпця знаходиться роздільна здатність.

На цьому етапі здійснюється до переходу до наступних ітерацій.

Перехід до ітерації:

Виводиться базис ключового рядка, поступаючись місцем змінної з ключового стовпця зі своїм коефіцієнтом.

Заповнюється рядок нововведеного базису шляхом поділу відповідних елементів виділеного рядка попередньої ітерації на роздільну здатність.

Якщо в головному рядку міститься нульовий елемент, то стовпець, в якому знаходиться цей елемент, переноситися в наступну ітерацію без зміни.

Якщо в головному стовпці є нульовий елемент, то рядок, в якому він знаходиться переноситься без зміни наступної ітерації.

Інші елементи переносяться за формулою: