4 Планування машинного експеременту
4.1 Планування машинного експерименту
Для раціонального проведення машинного експерименту доцільним є визначення початкових умов, необхідної кількості прогонів моделі та оцінки точності результатів. Для даної моделі припускаємо, що початковою умовою є відсутність будь-яких заявок в системі. Тобто, канал вільний, а в чергах немає транзактів.
Для визначення необхідної кількості прогонів моделі та оцінки її точності потрібно виконати кілька початкових прогонів для отримання деяких характеристик моделі [1]. Потрібно визначити ймовірність пропуску секції, середні та максимальні черги по кожному типу виробів. Для отримання цієї інформації було виконано десятикратну реалізацію моделі. Результати десятикратних реалізацій занесено до таблиці 4.1, де Pпр ймовірність пропуску секції, Qiср середня довжина черги для деталі і-ого типу, Qimax максимальна довжина черги для деталі і-ого типу.
Ймовірність пропуску секції розрахуємо за формулою:
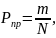(4.1)
де m – кількість пропусків секції,
N – загальна кількість секцій, які надійшли.
Таблиця 4.1 – Результати десятикратного прогону моделі
Експеримент № |
|
|
|
|
|
1 |
0,064 |
29,526 |
40 |
29,693 |
60 |
Продовження таблиці 4.1
Експеримент № |
|
|
|
|
|
2 |
0,043 |
23,819 |
30 |
23,993 |
50 |
3 |
0,043 |
18,55 |
30 |
20,697 |
50 |
4 |
0,043 |
17,32 |
25 |
32,148 |
30 |
5 |
0,085 |
35,562 |
55 |
10,864 |
30 |
6 |
0,043 |
10,624 |
20 |
12,503 |
30 |
7 |
0,085 |
24,046 |
40 |
13,397 |
40 |
8 |
0,064 |
30,615 |
40 |
13,277 |
30 |
9 |
0,064 |
29,974 |
40 |
15,03 |
40 |
10 |
0,064 |
27,2 |
40 |
13,358 |
30 |
Математичне очікування розраховується за формулою:
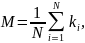(4.2)
де 𝑘𝑖 – параметр з множини, для якої необхідно розрахувати значення математичного сподівання,
N – кількість значень.
Дисперсію можна розрахувати за формулою:
.
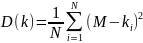(4.3)
Для розрахування значення середньоквадратичного відхилення за допомогою дисперсії можна скористатись формулою:
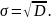(4.4)
Необхідно розрахувати похибку обчислень, щоб перевірити, чи не перевищує вона задану. Похибка розрахунків може бути обчислена за формулою:
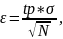(4.5)
де 𝑡𝑝 – табличний коефіцієнт, що відповідає заданій достовірності результатів, для достовірності 𝛼 = 0,95 значення коефіцієнта буде 𝑡𝑝 = 1,96.
Результати розрахунків математичного очікування, дисперсії, середньоквадратичного відхилення та похибки занесено до табл. 4.2.
Таблиця 4.2 – Результати розрахунків
Показник
|
|
|
|
|
|
Математичне очікування (М) |
0,0598 |
24,7236 |
36 |
18,496 |
39 |
Дисперсія (D) |
0,000247 |
50.19 |
89 |
68,46 |
109 |
Середньоквадратичне
відхилення ( |
0,015715 |
7.08 |
9.43 |
8,27 |
10,44 |
Похибка
( |
0,0097 |
4,39 |
5.84 |
5,12 |
6,47 |
)
)
З представленого вище можна зробити висновок, що тільки одне значення з усіх представлених не перевищують задане значення похибки 𝜀 = 0,5. За допомогою наступної формули можна виконати розрахунок необхідної кількості прогонів для отримання результатів із заданим значенням похибки:
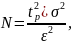(4.6)
де 𝑡𝑝 – табличний коефіцієнт, що відповідає заданій достовірності результатів, для достовірності 𝛼 = 0,95 значення коефіцієнта буде 𝑡𝑝 = 1,96. 𝜀 – задане значення похибки, у нашому випадку 0,5.
Таблиця 4.3 – Кількість прогонові
Показник
|
|
|
|
|
Кількість прогонів (N) |
297 |
226 |
405 |
644 |
Далі заплануємо машинний експеримент для визначення економічної доцільності переходу на інший режим роботи конвеєра, для цього змінемо необхідні параметри моделі, а саме, секції конвеєра будуть вміщувати по 20 деталей, час комплектування буде дорівнювати 20 хвилинам. Для даної моделі припускаємо, що початковою умовою є відсутність будь-яких заявок в системі. Тобто, канал вільний, а в чергах немає транзактів. Ймовірність пропуску секції, математичне очікування, дисперсію, похибку та кількість необхідних прогонів будемо рахувати за формулами (4.1 – 4.6). Усі розрахунки наведені у таблицях (4.4 – 4.6)
Таблиця 4.4 – Результати десятикратного прогону моделі
Експеримент № |
|
|
|
|
|
1 |
0,043 |
23,877 |
40 |
19,099 |
40 |
2 |
0,043 |
29,053 |
45 |
20,612 |
40 |
3 |
0,043 |
21,805 |
35 |
30,494 |
60 |
Продовження таблиці 4.4
Експеримент № |
|
|
|
|
|
4 |
0,043 |
32,399 |
45 |
26,816 |
40 |
5 |
0,043 |
28,178 |
45 |
13,192 |
40 |
6 |
0,043 |
29,458 |
45 |
25,744 |
60 |
7 |
0,043 |
23,735 |
40 |
20,109 |
40 |
8 |
0,041 |
25,058 |
40 |
23,008 |
40 |
9 |
0,043 |
22,529 |
35 |
37,357 |
60 |
10 |
0 |
15,167 |
30 |
21,374 |
40 |
Таблиця 4.5 – Результати розрахунків
Показник |
|
|
|
|
|
Математичне очікування (М) |
0,0385 |
25,1259 |
40 |
23,7805 |
46 |
Дисперсія (D) |
0,00016 |
21,68 |
25 |
85,74 |
84 |
Середньоквадратичне відхилення ( ) |
0,01284 |
4,65 |
5 |
9,259 |
9,1651 |
Похибка ( ) |
0,008 |
2,88 |
3,1 |
5,73 |
5,68 |
Таблиця 4.6 – Кількість прогонові
Показник |
|
|
|
|
Кількість прогонів (N) |
129 |
148 |
507 |
496 |
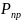
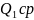
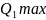
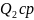
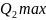
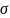
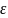