
- •Введение
- •1 Выбор конструкции верхнего строения пути. Построение поперечных профилей основной площадки земляного полотна и балластной призмы
- •1.1 Классификация железнодорожной линии и пути
- •1.1.1 Класс и специализация железнодорожной линии
- •1.1.2 Определение подгруппы, группы и класса пути
- •1.2 Выбор конструкции верхнего строения пути
- •1.3 Проектирование поперечных профилей основной площадки земляного полотна и балластной призмы
- •1.4 Вывод по первому разделу
- •2 Расчет основных параметров обыкновенного стрелочного перевода, укладываемого в стесненных условиях
- •2.1 Конструктивная схема обыкновенного стрелочного перевода
- •2.2 Расчетная геометрическая схема обыкновенного стрелочного перевода
- •2.3 Расчет основных параметров и разбивочных размеров обыкновенного стрелочного перевода, укладываемого в стесненных условиях.
- •2.3.1 Расчет радиуса переводной кривой, длины прямой вставки, малых и больших полуосей стрелочного перевода.
- •2.3.2 Определение ординат для разбивки переводной кривой стрелочного перевода
- •2.3.3 Определение длин рельсовых нитей стрелочного перевода
- •2.4 Вывод по второму разделу
- •3 Организация основных работ по капитальному ремонту пути
- •3.1 Определение вида работ
- •3.2 Установление схемы ремонтов пути и разработка календарного графика их проведения
- •3.3 Организация основных работ по капитальному ремонту пути
- •3.3.1 Общее положение
- •3.3.2 Назначение и характеристики путевых машин, принимаемых при работе по смене рельсошпальной решетки в «окно»
- •3.4 Определение длин технологических участков
- •3.5 Определение интервалов времени между отдельными операциями
- •3.6 Вывод по третьему разделу
- •4 Организация снегоборьбы на станции
- •4.1 Определение объема снега, подлежащего уборке
- •4.2 Определение продолжительности очистки станции от снега
- •4.3 Вывод по четвертому разделу
- •Заключение
- •Список использованных источников
- •Приложение а
- •Приложение б
2.3 Расчет основных параметров и разбивочных размеров обыкновенного стрелочного перевода, укладываемого в стесненных условиях.
2.3.1 Расчет радиуса переводной кривой, длины прямой вставки, малых и больших полуосей стрелочного перевода.
Если при укладке стрелочных переводов в стесненных условиях необходимо уменьшить теоретическую длину типового перевода более чем на 250 мм, следует выполнить перерасчет его основных параметров и разбивочных размеров.
Основные характеристики обыкновенного стрелочного перевода типа Р65 марки 1/9 принимаем из таблицы 2.1 [1].
Теоретическая длина стрелочного перевода Lт, мм, с учетом уменьшения его длины на Δ, мм, определяется по формуле
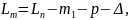 (2.1)
(2.1)
где Lп – полная длина стрелочного перевода, мм;
m1 – передний вылет рамного рельса, мм;
p – задний вылет крестовины, мм;
Δ – требуемое укорочение стрелочного перевода, мм.
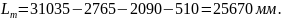
Практическая длина стрелочного перевода после его укорочения Lп.у рассчитывается по формуле
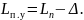 (2.2)
(2.2)
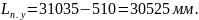
Угол между рабочими гранями крестовины α, рад, определяется по формуле
 (2.3)
(2.3)
где
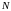 – знаменатель марки крестовины.
– знаменатель марки крестовины.
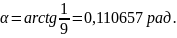
Полный стрелочный угол βп, рад, вычисляется по формуле
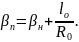 (2.4)
(2.4)
где βн – начальный угол остряка, рад;
l0 – длина криволинейного остряка, мм;
R0 – радиус остряка, мм.
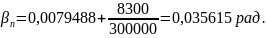
Проекция криволинейного остряка на рамный рельс , мм, определяется по формуле (2.5)
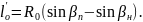 (2.5)
(2.5)
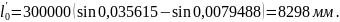
Ордината в корне остряка вычисляется по формуле (2.6)
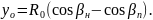 (2.6)
(2.6)
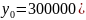
Длина прямого рамного рельса складывается из проекции криволинейного остряка на него, переднего и заднего вылетов, а также от принятого типа корневого крепления (рисунок 2.2)
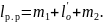 (2.7)
(2.7)
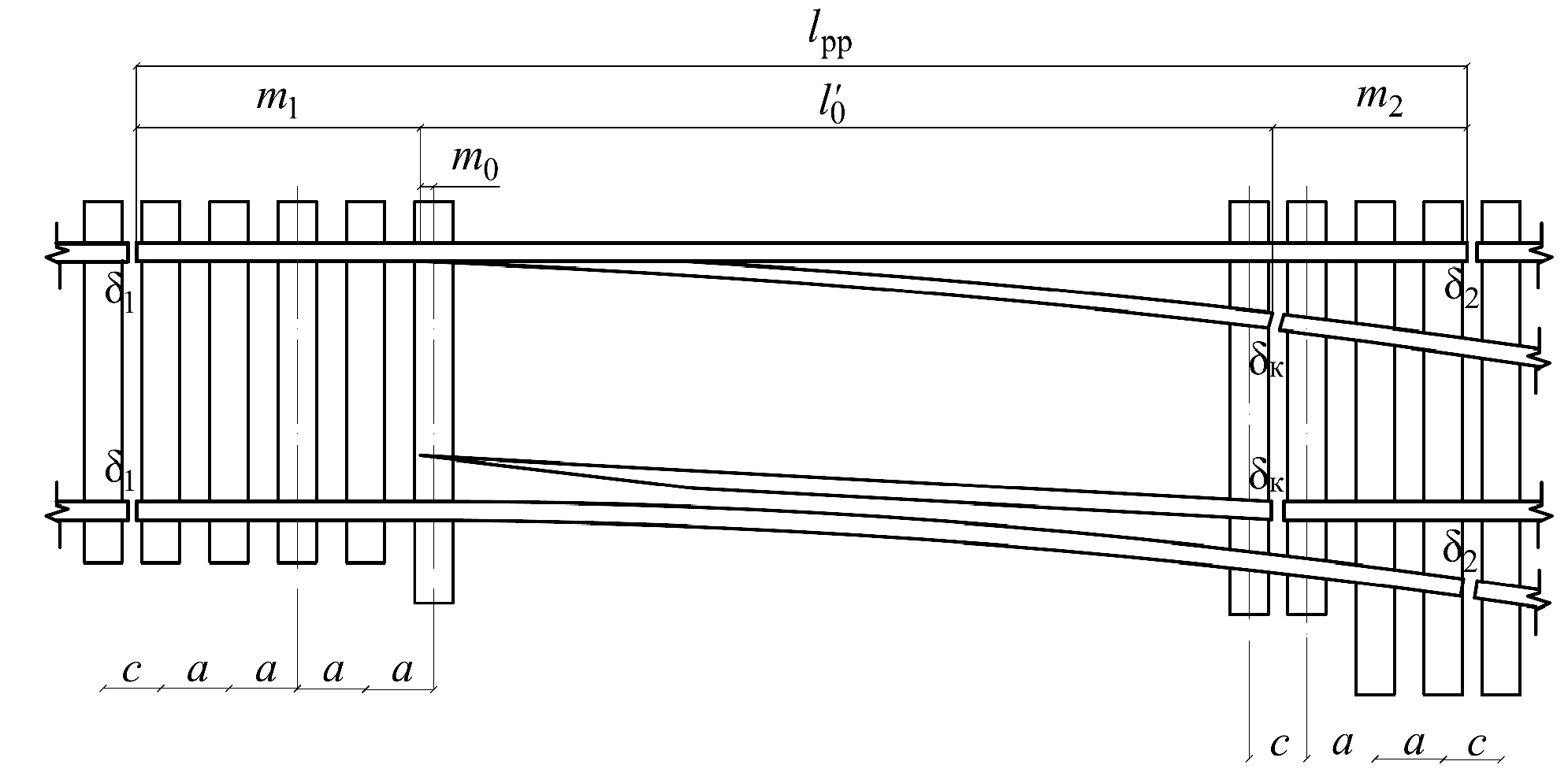
Рисунок 2.2 – Схема стрелочной части
Тогда задний вылет рамного рельса составит
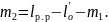 (2.8)
(2.8)
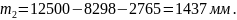
Укороченный радиус переводной кривой Ry определяется по формуле (2.9)
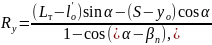 (2.9)
(2.9)
где S – ширина колеи по прямому направлению стрелочного перевода, мм.
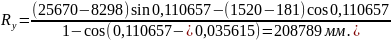
Длина прямой вставки d определяется по формуле
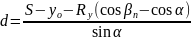 . (2.10)
. (2.10)
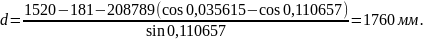
Малые полуоси стрелочного перевода вычисляются по формулам (2.11) и (2.12)
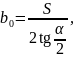 (2.11)
(2.11)
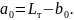 (2.12)
(2.12)
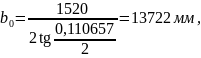
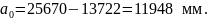
Большие полуоси определяются по формулам (2.13) и (2.14)
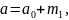 (2.13)
(2.13)
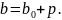 (2.14)
(2.14)
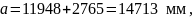
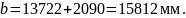
Расстояния, определяющие положение предельного столбика, вычисляются по формулам (2.15) - (2.17). Схема расположения предельного столбика показана на рисунке 2.3.
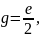 (2.15)
(2.15)
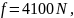 (2.16)
(2.16)
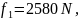 (2.17)
(2.17)
где g − расстояние от предельного столбика до оси пути, мм;
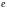 − расстояние между осями путей в месте
установки предельного столбика, мм,
равное 4100 мм;
− расстояние между осями путей в месте
установки предельного столбика, мм,
равное 4100 мм;
f, f1 − расстояния от предельного столбика до ЦП и МЦ соответственно, мм.
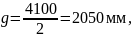
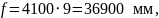
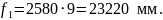
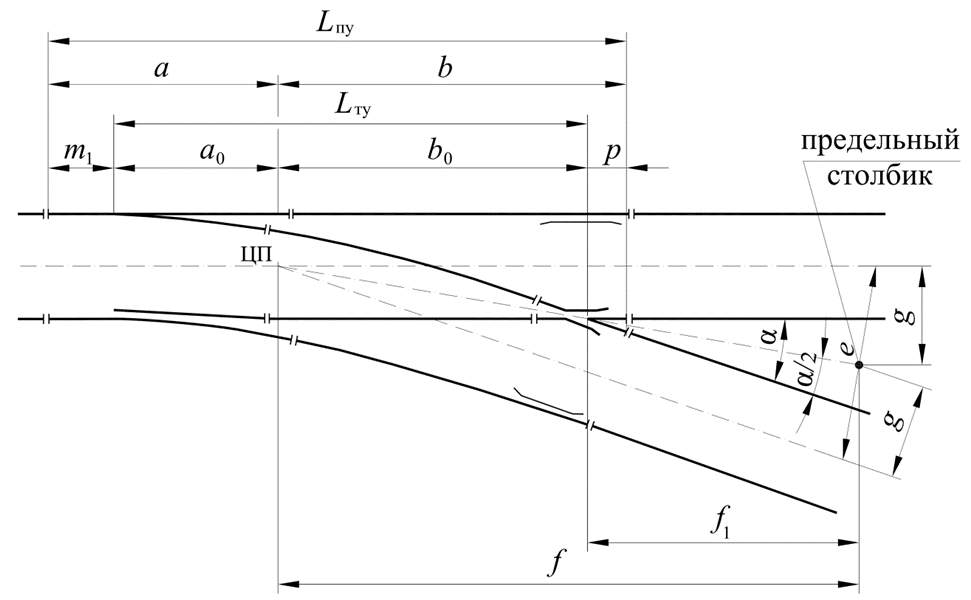
Рисунок 2.3 – Схема стрелочного перевода с основными и осевыми размерами и предельным столбиком
2.3.2 Определение ординат для разбивки переводной кривой стрелочного перевода
При разбивке переводной кривой за начало координат принимается точка А, расположенная на рабочей грани рамного рельса напротив корня остряка (рисунок 2.4).
Координаты конца переводной кривой хк и ук, мм, определяются по формулам
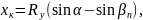 (2.18)
(2.18)
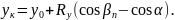 (2.19)
(2.19)
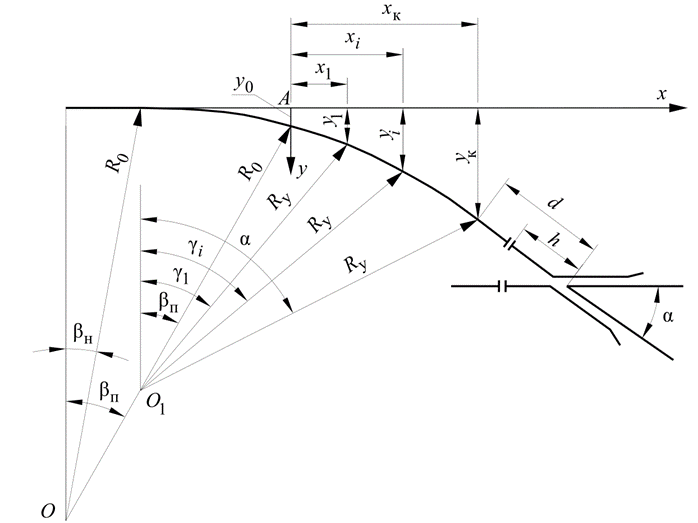
Рисунок 2.4 – Расчетная схема для определения ординат переводной кривой
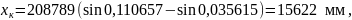
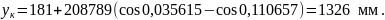
Координаты промежуточных точек
определяются следующим образом. По оси
абсцисс значения
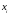 назначаются с шагом 2000 мм от х0
= 0 до хк,
а ординаты yi
определяются по формуле
назначаются с шагом 2000 мм от х0
= 0 до хк,
а ординаты yi
определяются по формуле
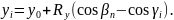 (2.20)
(2.20)
Значение i определяется из зависимости
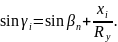 (2.21)
(2.21)
При этом должно выполняться равенство
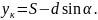 (2.22)
(2.22)
Расчеты удобно проводить в табличной форме. Результаты расчета последующих ординат сведены в таблицу 2.1.
Таблица 2.1 – Расчет ординат переводной кривой
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
0 |
0 |
0,035607 |
0,035615 |
0,999366 |
181 |
2000 |
0,009579 |
0,045187 |
0,045202 |
0,998979 |
262 |
4000 |
0,019158 |
0,054766 |
0,054793 |
0,998499 |
362 |
6000 |
0,028737 |
0,064345 |
0,064389 |
0,997928 |
481 |
8000 |
0,038316 |
0,073924 |
0,073991 |
0,997264 |
620 |
Продолжение таблицы 2.1
1 |
2 |
3 |
4 |
5 |
6 |
10000 |
0,047895 |
0,083503 |
0,083600 |
0,996508 |
778 |
12000 |
0,057474 |
0,093082 |
0,093217 |
0,995658 |
955 |
14000 |
0,067053 |
0,102661 |
0,102842 |
0,994716 |
1152 |
15622 |
0,074822 |
0,110429 |
0,110655 |
0,993884 |
1326 |
Проверка: значение конечной ординаты, вычисленной по формуле (2.19), должно совпадать со значением, полученным в таблице 2.1:
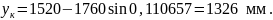
Следовательно, условие выполняется.

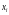 ,
мм
,
мм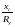
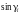
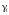 ,
рад
,
рад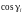
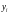 ,
мм
,
мм