ЛЕКЦИЯ 10. ПРИБЛИЖЕНИЕ ФУНКЦИЙ

ЛИТЕРАТУРА. Учебник [1] §§11.3, 11.4, 11.7

[2] §§1,2

В лекции 9 были приведены две постановки задачи о приближении таблично заданной функции: приближение в «среднем» и приближение методом интерполяции.

Постановка задачи о приближении в среднем. Пусть даны точки , , … и известны значения исходной функции в этих точках , . Требуется найти такую аппроксимирующую функцию , чтобы величина среднеквадратичного отклонения (СКО)

(10.1)

была минимальной.

В предыдущей лекции эта задача была решена в случае, когда функция

представляла собой многочлен степени m. Рассмотрим решение задачи в общем случае.

§10.1 Приближение функции по мнк обобщенным многочленом

Пусть функция представляет собой обобщенный многочлен:

(10.2)

Запишем его в более компактном виде:

Задача состоит в том, чтобы найти такие коэффициенты , , … , чтобы величина

СКО (10.1) была минимальной.

Будем решать задачу аналогично решению задачи приближения многочленами. Заметим, что при фиксированной степени среднеквадратичное отклонение является функцией коэффициента многочлена . Минимум среднеквадратичного отклонения достигается при тех же значениях , что и минимум функции:

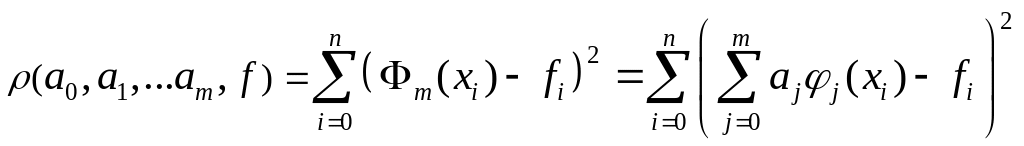
Запишем необходимое условие экстремума функции нескольких переменных:

, k=0,1,…m

Дифференцируя функцию по коэффициенту , получим следующее выражение:

Меняя порядки суммирования, получим систему алгебраических уравнений относительно

неизвестных , к=0,1,…m. В общем виде система выглядит так:

, k=0,…m (10.3)

Можно записать ее в более развернутом виде:

ПРИМЕР 10.1. Пусть функция задана таблицей:

x	-1	0	1
f(x)	0.5	1.5	2

Известно, что функция имеет вид: . Найти коэффициенты a и b.

Решение. Функция f(x) задана обобщенным многочленом

, . Составим нормальную систему метода наименьших квадратов.

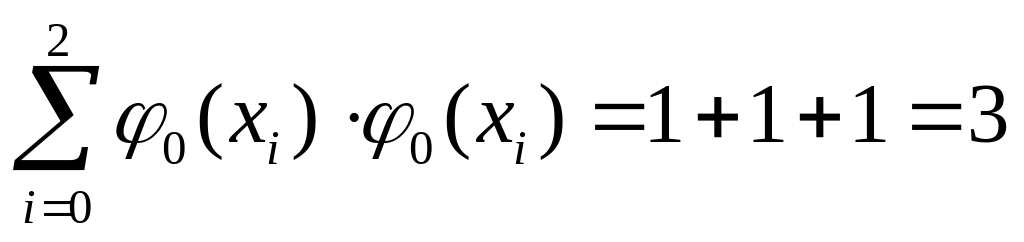
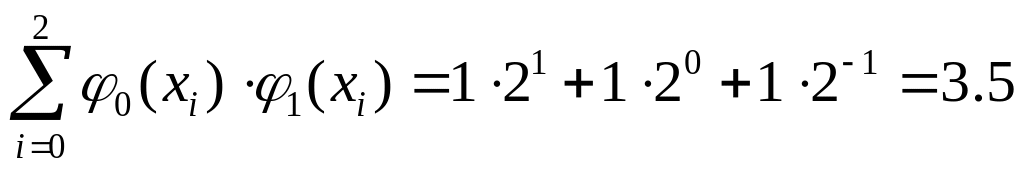
Найдем правую часть:

,

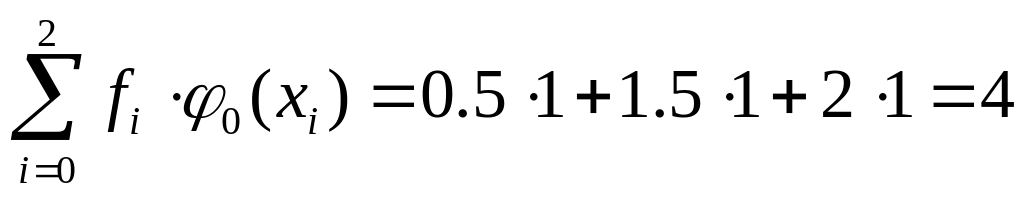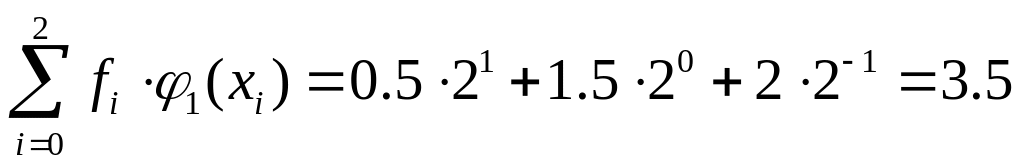
Получаем систему уравнений

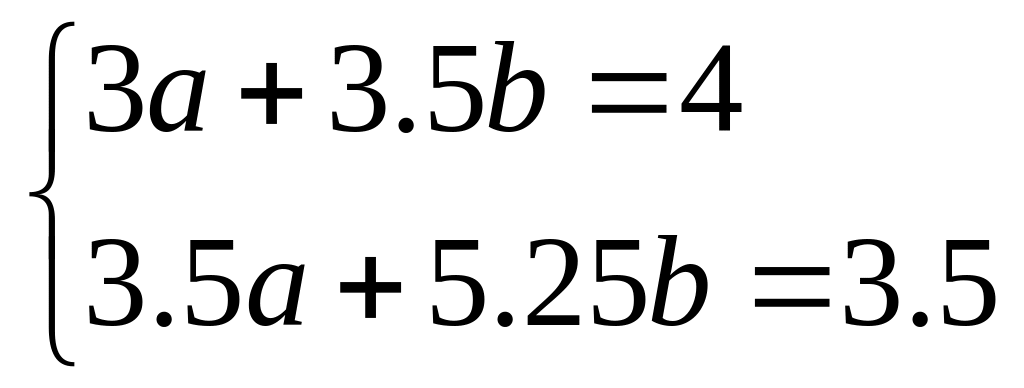
, . Таким образом, . При этом СКО=0

§10.2. Многочлен лагранжа.

Пусть функция задана на множестве дискретных точек , , … , предполагаем дополнительно, что при . Задача интерполяции состоит в построении функции такой, что , .

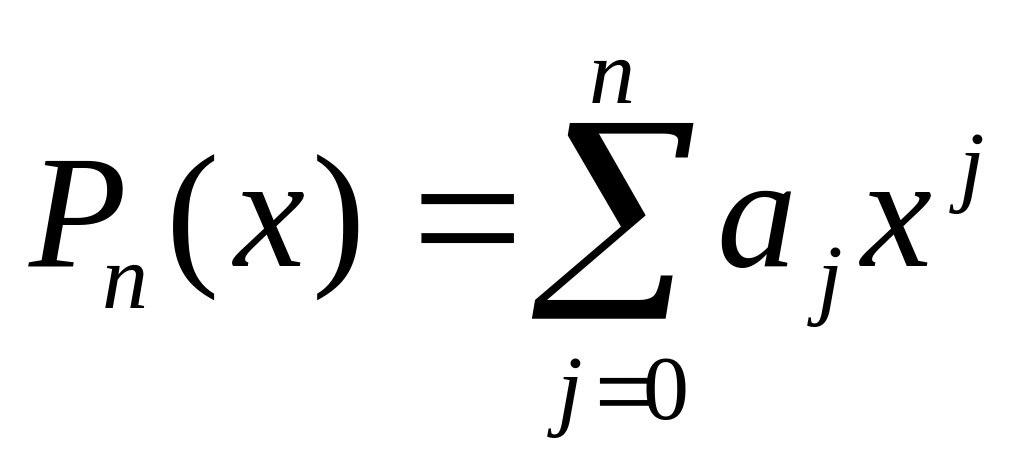Будем приближать функцию интерполяционным многочленом степени n. ОПРЕДЕЛЕНИЕ. Многочлен степени n, удовлетворяющий условию , называется интерполяционным многочленом.

Заметим, что многочлен содержит n+1 неизвестный коэффициент . Можно написать такую систему равенств, состоящих из n+1 уравнения:

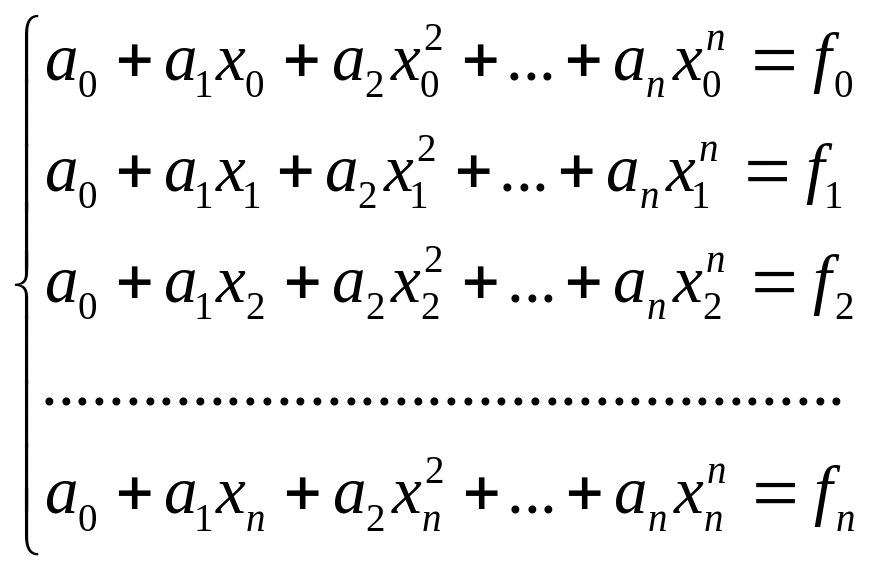(10. 4)

ТЕОРЕМА 10.1. Интерполяционный многочлен существует и единственен.

Доказательство. Система (10.4) имеет единственное решение. Действительно, рассмотрим определитель системы :

Это есть определитель Вандермонда. Если среди узлов интерполяции нет одинаковых, то

он не равен нулю. Выше было сделано предположение, что при .

По теореме Крамера: если матрица квадратной системы линейных уравнений невырождена, то решение системы существует и единственно. Ч.т.д.

ПРИМЕР 10.2. Приблизим функцию из примера 10.1 интерполяционным многочленом. Так как функция задана значениями в 3-х точках решим задачу интерполяции, приближая функцию многочленом второй степени.

Подставим узлы интерполяции и значения функции из таблицы для нахождения коэффициентов многочлена:

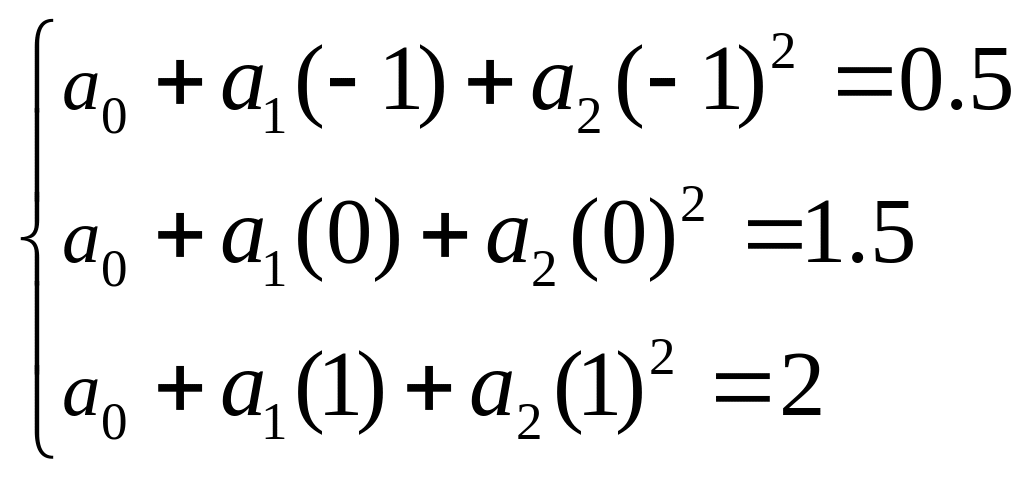Тогда :

На практике в редких случаях для нахождения коэффициентов многочлена решают

систему (10.4). Обычно используют другие формы записи многочленов.

Рассмотрим многочлен следующего вида:

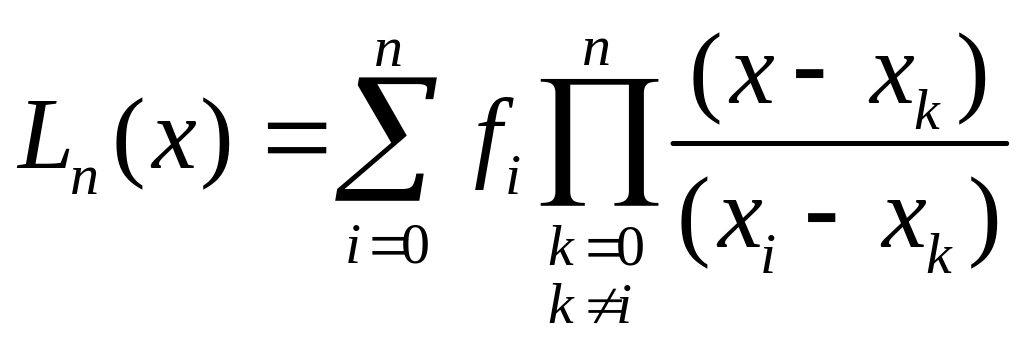(10.5)

Эта форма записи интерполяционного многочлена называется многочленом Лагранжа.

Запишем два частных случая этого многочлена довольно часто встречающихся в практике

Линейная интерполяция. Пусть функция задана значениями в двух точках:

x
f(x)

Тогда многочлен Лагранжа примет вид:

Квадратичная интерполяция. Пусть функция задана значениями в трех точках:

x
f(x)

Тогда многочлен Лагранжа примет вид:

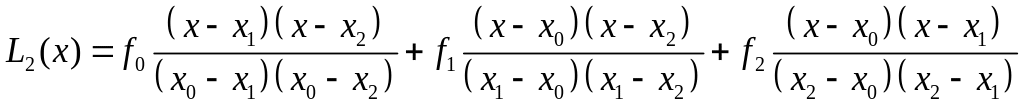
Таким образом, (10.5) - многочлен представляет собой сумму n+1 слагаемого, каждое из которых есть многочлен степени n. Подставим в узел . Заметим, что к-ое слагаемое при обращается в ноль, а при числитель и знаменатель дроби совпадают и мы получаем значение . Таким образом, (10.5) представляет собой интерполяционный многочлен.

ПРИМЕР 10.3. Рассмотрим задачу вычисления функции для значений и . Эту задачу будем решать методом интерполяции. Приблизим исходную функцию на отрезке [9,16] многочленом Лагранжа 1-ой степени. Для этого возьмем два узла интерполяции и . Тогда и .

Составим многочлен по формуле (10.5):

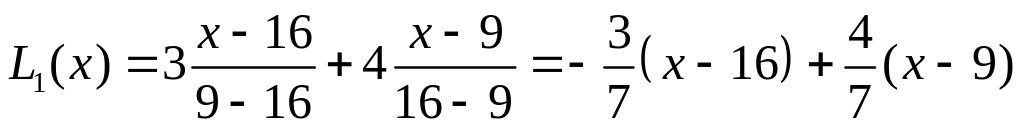
Теперь вычислим значения в указанных точках:

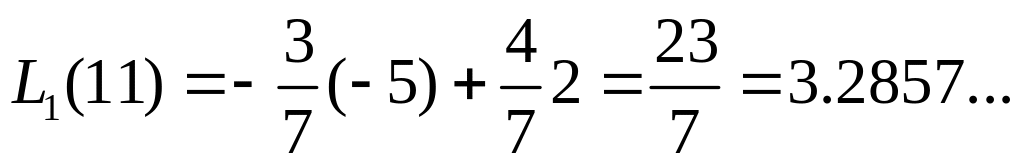, для сравнения значение ,

Аналогично для 2-го числа

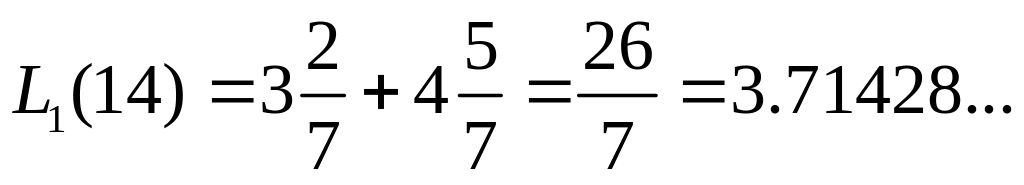, для сравнения значение