
Все за 2й курс / Отчет ЛР5
.docxЗадача 5.1
Постановка
задачи: Вычислить
значение интеграла
 ,
где
,
где
 ,
с помощью элементарных квадратурных
формул левых прямоугольников и по
формуле индивидуального варианта.
Затем, используя априорную оценку
погрешности, оценить шаг интегрирования
h,
требуемый для достижения точности
,
с помощью элементарных квадратурных
формул левых прямоугольников и по
формуле индивидуального варианта.
Затем, используя априорную оценку
погрешности, оценить шаг интегрирования
h,
требуемый для достижения точности .Вычислить
интеграл с найденным шагом интегрирования.
.Вычислить
интеграл с найденным шагом интегрирования.
Решение задачи:
Входные
данные:
![]()
![]()
![]()
![]()
График функциии P(x):

Вычислим интеграл с помощью средств МС:
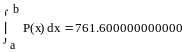

Для оценки шага интегрирования воспользуемся теоретической оценкой погрешности:
Найдем константу М4 используя МС:
![]()
![]()

![]()
Для нахождения шага воспользуемся априорной оценкой погрешности:
![]()
Найдем шаг интегрирования требуемый для достижения заданной точности έ
![]()
Переопределим значение n: n:=34288000
Скорректируем шаг интегрирования:
![]()
В
ы ч и с л и м з н а ч е н и е и н т е г р а
л а п о с о с т а в н о й ф о р м у л е л е
в ы х п р я м о у г о л ь н и к о в :

![]()
П о л у ч е н н а я в е л и ч и н а п о г р е ш н о с т и :
![]()
Д Л Я В Ы Ч И С Л Е Н И Я И Н Т Е Г Р А Л А В О С П О Л Ь З У Е М С Я Ф О Р М У Л О Й
8-г о П О Р Я Д К А Т О Ч Н О С Т И
![]()
![]()
![]()
Найденное точное значение интеграла
|
Число разбиений отрезка n Шаг интегрирования h |
Значение
интеграла, вычисленное по составной
формуле
Величина
погрешности интеграла, вычисленного
по составной формуле
|
Метод Левых прямоугольников |
n:=34288000 h:= 0.00000058343057176 |
Ih:= 761.599629988383 Rh:= 0.00037001161717853 |
Метод индивидуального варианта Метод Виделла |
n:=1 h:=2 |
Ih:= 761.6000000000003 Rv:= 0.00000000000011369 |
Задача
5.2. Вычислить
интеграл
 с точностью
с точностью

ПОРЯДОК РЕШЕНИЯ ЗАДАЧИ
1.
Вычислить интеграл
 с помощью средств
пакета MATHCAD
.
с помощью средств
пакета MATHCAD
.
2. Составить программу, содержащую следующие разделы:
а)
процедуру-функцию, вычисляющую интеграл
по составной квадратурной формуле из
индивидуального варианта
 с заданным шагом h.
с заданным шагом h.
б)
подпрограмму, вычисляющую значение
интеграла с заданной точностью
 ;
оценку погрешности производить на
основе правила Рунге.
;
оценку погрешности производить на
основе правила Рунге.
с)
вычисление уточненного значение
интеграла и величину погрешности
и величину погрешности
Результатом работы программы должны быть следующие величины:
n- число разбиений отрезка интегрирования, при котором заданная точность
достигнута,
и
- - полученные значения интеграла при
шагах
- полученные значения интеграла при
шагах и
и
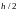 соответственно,
соответственно,
 и
и
 - величины абсолютных погрешностей,
- величины абсолютных погрешностей,
 и
и
 - величины для уточненного значения
интеграла.
- величины для уточненного значения
интеграла.
4.Вычислить интеграл по программе и полученные данные свести в таблицу 5.2
Входные данные:
![]()
![]()
![]()
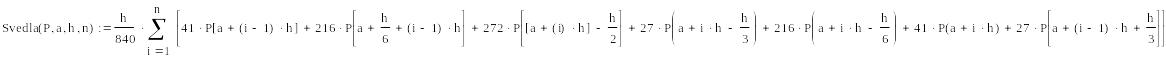

Результаты вычислений:

I= -2.6387190477252433 |
Метод индивидуального варианта Метод Ведлла |
Число разбиений отрезка
Значение интеграла
Величина погрешности
Уточненное значение интеграла
|
=1.4587915056926417
|




 16
16
 =1.4587915056927052
=1.4587915056927052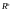 =0.00000000000006345
=0.00000000000006345