
Лабораторная работа 5 численное интегрирование
Теоретический материал к данной теме содержится в [1, глава 13].
Варианты заданий к задачам 5.1–5.2 даны в ПРИЛОЖЕНИИ 5.A.
Требования к лабораторной работе 5
Задачи 5.1 и 5.2 выполняются с помощью пакета MATHCAD.
Задача
5.1. Вычислить значение интеграла
 ,
где
,
где
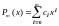 ,
с помощью элементарных квадратурных
формул левых прямоугольников и по
формуле индивидуального варианта.
Затем, используя априорную оценку
погрешности, оценить шаг интегрирования
h, требуемый для достижения
точности
,
с помощью элементарных квадратурных
формул левых прямоугольников и по
формуле индивидуального варианта.
Затем, используя априорную оценку
погрешности, оценить шаг интегрирования
h, требуемый для достижения
точности
 .
Вычислить интеграл с найденным шагом
интегрирования.
.
Вычислить интеграл с найденным шагом
интегрирования.
Порядок решения задачи
1.
Используя средства пакета МС, вычислить
значение интеграла
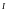 .
.
2.
Используя выражение для остаточного
члена интегрирования (см. ПРИЛОЖЕНИЕ
5.B), оценить шаг
интегрирования h , при
котором величина погрешности квадратурной
формулы будет меньше
 .
Вычислить число отрезков разбиения n.
.
Вычислить число отрезков разбиения n.
3.
Вычислить значение интеграла
 по составной квадратурной формуле
левых прямоугольников с найденным
шагом
по составной квадратурной формуле
левых прямоугольников с найденным
шагом
 .
Найти величину погрешности
.
Найти величину погрешности
 .
.
4. Проделать те же действия (п. 2 - 3) для вычисления интеграла по квадратурной формуле из индивидуального варианта.
5. Результаты внести в таблицу. (В приложении часть таблицы 5.1 заполнена для нулевого варианта, см. файл МС).
Задача
5.2. Вычислить интеграл
 с точностью
с точностью
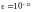
Порядок решения задачи
1. Вычислить интеграл с помощью средств пакета MATHCAD .
2. Составить программу, содержащую следующие разделы:
а)
процедуру-функцию, вычисляющую интеграл
по составной квадратурной формуле из
индивидуального варианта
 с заданным шагом h.
с заданным шагом h.
б) подпрограмму, вычисляющую значение интеграла с заданной точностью ; оценку погрешности производить на основе правила Рунге.
с) вычисление
уточненного значение интеграла и величину погрешности
и величину погрешности
Результатом работы программы должны быть следующие величины:
n- число разбиений отрезка интегрирования, при котором заданная точность
достигнута,
и - - полученные значения интеграла при
шагах
- полученные значения интеграла при
шагах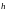 и
и
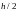 соответственно,
соответственно,
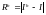 и
и
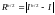 - величины абсолютных погрешностей,
- величины абсолютных погрешностей,
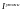 и
и
 - величины для уточненного значения
интеграла.
- величины для уточненного значения
интеграла.
4.Вычислить интеграл по программе и полученные данные свести в таблицу 5.2 .
Оформить отчет по ЛР, содержащий постановки задач, расчетные формулы вариантов и заполненные таблицы 5.1 и 5.2.
Приложение 5.A варианты заданий к лабораторной работе 5
ВНИМАНИЕ!
Номер варианта
 для лабораторных работ вычисляется
по следующей формуле:
для лабораторных работ вычисляется
по следующей формуле:
1)
 для групп 9–11;
для групп 9–11;
2) Для групп 12–15
(здесь
 — номер группы, а
— номер группы, а
 — индивидуальный номер студента по
журналу).
— индивидуальный номер студента по
журналу).
Примечание.
Если полученный номер
получился больше значения 50, то принять

Если
полученный номер
получился меньше 1, то принять

Таблица к задаче 5.1
|
|
|
|
|
|
|
|
|
|
|
|
|
5.1.1 |
0.6 |
1.3 |
0 |
1.2 |
1.9 |
5.1.27 |
3.5 |
–0.2 |
–2.3 |
–3.1 |
3.1 |
1.6 |
5.1.2 |
1 |
0.9 |
0.8 |
0.7 |
0.5 |
5.1.28 |
2.2 |
–4.1 |
0.3 |
–3.4 |
3.5 |
2.3 |
5.1.3 |
0.4 |
0.3 |
0.2 |
0.1 |
2 |
5.1.29 |
0.8 |
6.5 |
–4.4 |
6.1 |
–3.6 |
2.3 |
5.1.4 |
0.1 |
–0.1 |
1 |
1 |
1 |
5.1.30 |
7.9 |
–0.4 |
2.7 |
0.7 |
–2.4 |
–4.1 |
5.1.5 |
1.5 |
0 |
–2.1 |
–1.1 |
3.1 |
5.1.31 |
1.3 |
0.5 |
2.1 |
5.7 |
8.3 |
5.2 |
5.1.6 |
–2.5 |
–2.1 |
0 |
0.4 |
0.5 |
5.1.32 |
–5.6 |
–7.2 |
1.5 |
4.6 |
–5.1 |
6.5 |
5.1.7 |
6.8 |
1.7 |
–4.1 |
0.1 |
–6.1 |
5.1.33 |
7.4 |
–2.3 |
6.6 |
0.3 |
1.8 |
2.4 |
5.1.8 |
0 |
1.4 |
3.2 |
1.6 |
–9.4 |
5.1.34 |
4.4 |
15 |
–3.3 |
2.4 |
5.3 |
–2.7 |
5.1.9 |
1.3 |
0 |
–0.1 |
0.7 |
8.1 |
5.1.35 |
1.8 |
–2.4 |
5.5 |
7.4 |
–3.3 |
–3.7 |
5.1.10 |
2.8 |
–1.2 |
–1.5 |
0 |
6.4 |
5.1.36 |
6.6 |
–3.7 |
–8.4 |
5.5 |
15 |
–2.1 |
5.1.11 |
5.4 |
2.1 |
0.3 |
2.1 |
1.6 |
5.1.37 |
4.8 |
1.5 |
6.3 |
–2.7 |
3.7 |
4.4 |
5.1.12 |
0 |
–2.9 |
–0.9 |
0.4 |
1.9 |
5.1.38 |
0.6 |
1.3 |
0 |
1.2 |
1.9 |
5.2 |
5.1.13 |
5.2 |
5.3 |
2.5 |
0.1 |
0 |
5.1.39 |
1 |
0.9 |
0.8 |
0.7 |
0.5 |
–6.0 |
5.1.14 |
–4.6 |
–0.4 |
1.6 |
0 |
2.4 |
5.1.40 |
0.4 |
0.3 |
0.2 |
0.1 |
2 |
3.7 |
5.1.15 |
3.5 |
–0.2 |
–2.3 |
–3.1 |
3.1 |
5.1.41 |
0.1 |
–0.1 |
1 |
1 |
1 |
2.1 |
5.1.16 |
2.2 |
–4.1 |
0.3 |
–3.4 |
3.5 |
5.1.42 |
1.5 |
0 |
–2.1 |
–1.1 |
3.1 |
–4.3 |
5.1.17 |
0.8 |
6.5 |
–4.4 |
6.1 |
–3.6 |
5.1.43 |
–2.5 |
–2.1 |
0 |
0.4 |
0.5 |
5.7 |
5.1.18 |
7.9 |
–0.4 |
2.7 |
0.7 |
–2.4 |
5.1.44 |
6.8 |
1.7 |
–4.1 |
0.1 |
–6.1 |
8.4 |
5.1.19 |
1.3 |
0.5 |
2.1 |
5.7 |
8.3 |
5.1.45 |
0 |
1.4 |
3.2 |
1.6 |
–9.4 |
–13 |
5.1.20 |
–5.6 |
–7.2 |
1.5 |
4.6 |
–5.1 |
5.1.46 |
1.3 |
0 |
–0.1 |
0.7 |
8.1 |
11.2 |
5.1.21 |
7.4 |
–2.3 |
6.6 |
0.3 |
1.8 |
5.1.47 |
2.8 |
–1.2 |
–1.5 |
0 |
6.4 |
5.6 |
5.1.22 |
4.4 |
15 |
–3.3 |
2.4 |
5.3 |
5.1.48 |
5.4 |
2.1 |
0.3 |
2.1 |
1.6 |
1.4 |
5.1.23 |
1.8 |
–2.4 |
5.5 |
7.4 |
–3.3 |
5.1.49 |
0 |
–2.9 |
–0.9 |
0.4 |
1.9 |
–4.2 |
5.1.24 |
6.6 |
–3.7 |
–8.4 |
5.5 |
15 |
5.1.50 |
5.2 |
5.3 |
2.5 |
0.1 |
0 |
3.8 |
5.1.25 |
–0.5 |
0 |
1.3 |
7.1 |
0 |
5.1.51 |
3.4 |
–1.6 |
4.5 |
2.8 |
4.5 |
–7.4 |
5.1.26 |
4.8 |
1.5 |
6.3 |
–2.7 |
3.7 |
5.1.52 |
–4.6 |
–0.4 |
1.6 |
0 |
2.4 |
7.1 |
Таблица к задаче 5.2
|
f(x) |
[a,b] |
|
f(x) |
[a,b] |
5.1.1 |
|
[2,6] |
5.1.26 |
|
[2,7] |
5.1.2 |
|
[-1,3] |
5.1.27 |
|
[0.1,7] |
5.1.3 |
|
[2,6] |
5.1.28 |
|
[2,6] |
5.1.4 |
|
[-2,1] |
5.1.29 |
|
[7,11] |
5.1.5 |
|
[5,8] |
5.1.30 |
|
[-3,0] |
5.1.6 |
|
[9,16] |
5.1.31 |
|
[-2,2] |
5.1.7 |
|
[-3,0] |
5.1.32 |
|
[6,10] |
5.1.8 |
|
[1,9] |
5.1.33 |
|
[-1,1] |
5.1.9 |
|
[7,11] |
5.1.34 |
|
[7,20] |
5.1.10 |
|
[0,6] |
5.1.35 |
|
[-8,0] |
5.1.11 |
|
[3,5] |
5.1.36 |
|
[0,10] |
5.1.12 |
|
[0,3] |
5.1.37 |
|
[-6,1] |
5.1.13 |
|
[3,8] |
5.1.38 |
|
[-2,1] |
5.1.14 |
|
[5,16] |
5.1.39 |
|
[-2,4] |
5.1.15 |
|
[2,6] |
5.1.40 |
|
[1,9] |
5.1.16 |
|
[1,10] |
5.1.41 |
|
[8,12] |
5.1.17 |
|
[-4,0] |
5.1.42 |
|
[-5,0] |
5.1.18 |
|
[-1,4] |
5.1.43 |
|
[9,16] |
5.1.19 |
|
[-2,2] |
5.1.44 |
|
[2,6] |
5.1.20 |
|
[4,7] |
5.1.45 |
|
[-6,0] |
5.1.21 |
|
[-3,0] |
5.1.46 |
|
[4,7] |
5.1.22 |
|
[-2,2] |
5.1.47 |
|
[0,3] |
5.1.23 |
|
[1,6] |
5.1.48 |
|
[-4,0] |
5.1.24 |
|
[0.1,5] |
5.1.49 |
|
[-3,0] |
5.1.25 |
|
[-2,2] |
5.1.50 |
|
[-3,1] |
рианты |
Метод решения |
|
(3) формула центральных прямоугольников |
2,8,14,20,26,32,38,44,50 |
(4) формула трапеций |
3,9,15,21,27,33,39,45,51 |
(5) формула Симпсона |
4,10,16,22,28,34,40,46,52 |
(6) правило 3/8 |
5,11,17,23,29,35,41,47 |
(7) формула Милна |
6,12,18,24,30,36,42,48 |
(8) формула Вэддла |

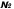
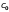



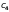

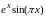
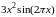
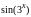




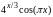



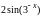
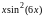



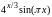
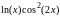



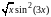
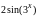
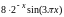


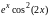
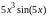

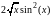


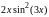














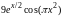

 1,7,13,19,
25,31,37,43,49
1,7,13,19,
25,31,37,43,49