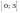Все за 2й курс / ЛР2

Задача 2.1. Дано уравнение f(x)=0. Найти с точностью 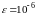все корни уравнений, содержащиеся на отрезке [с, d]. Для решения задачи использовать метод бисекции. Найти корни с помощью встроенной функции root пакета MATHCAD.

2.1.22

Аналитическое решение задачи:

f(x)=(cosx+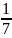 )(cosx- 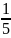) Cos x=-1/7; x1=arcos(-1/7)= 1.714143895700262;

x2=π-arcos(1/5)= 1.7721542475852274;

Численный метод решения задачи:

Локализация корней для численного решения задачи:

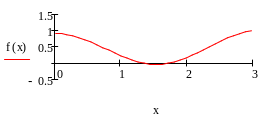
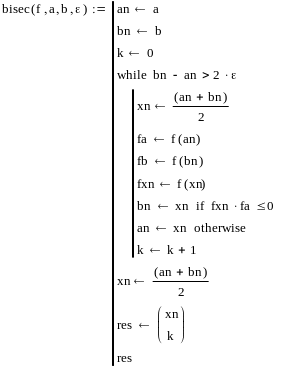
Встроенная функция пакета MATHCAD

X=1- задание начального приближения

Значение корня отличается от найденного с помощью функции bisec , так как по умолчанию величина погрешности при работе встроенных функций равна 0.001.

Переопределим параметр для задания погрешности

Значение корня с заданной точностью 1.3694384060034341

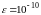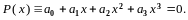Задача 2.2. Найти с точностью вещественные корни алгебраического уравнения В программе предусмотреть подсчет количества итераций.

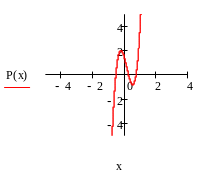
З а д а ч а 2.2

О т р е з о к л о к а л и з а ц и и [1,2]

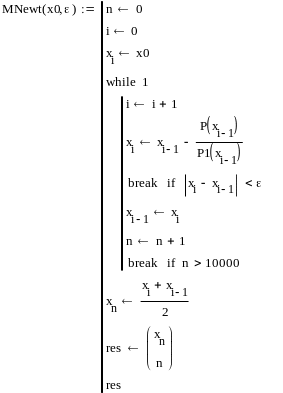
Метод ложного положения

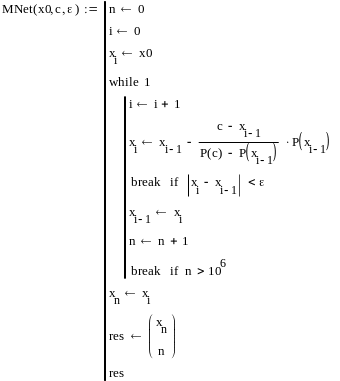
Значения в методе ньютона и методе ложного положения практически совпадают но в методе ложного положения большее количество итераций.