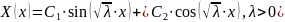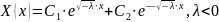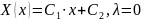Все за 2й курс / Лекция 10
.docxЛекция 10 . Численное решение начально-краевой задачи
для уравнения теплопроводности.
Литература к лекции. Казенкин К.O., Амосова О.А.. Численное решение задач математической физики. Нестационарные уравнения .М: Изд-во МЭИ, 2016.
§ 10.1 Постановка задачи
Будем рассматривать первую краевую задачу с постоянными коэффициентами для уравнения теплопроводности.
 (10.1)
(10.1)
Задача (10.1) описывает процесс распространения тепла в стержне длины L. Функция
u(x,t)
имеет смысл температуры стержня в точке
x
в момент времени t,
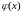 -
начальная температура стержня в момент
-
начальная температура стержня в момент
 ,
,
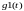 ,
,
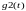 - граничные функции, задающие значения
температуры в левой точке
- граничные функции, задающие значения
температуры в левой точке
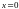 и в правой точке
и в правой точке
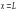 соответственно. Функция
соответственно. Функция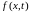 называется функцией плотности внешних
источников.
называется функцией плотности внешних
источников.
Напомним, как решается данная задача аналитически в самых простых случаях.
Для
начала возьмем однородные краевые
условия
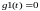 и
и
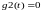 правую
часть
правую
часть
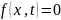 .
Будем искать решение методом Фурье,
то есть представим решение в виде
произведения двух функций:
.
Будем искать решение методом Фурье,
то есть представим решение в виде
произведения двух функций:
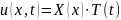 ,
одна из которых зависит только от x, а
другая от t.
Тогда, подставив
предполагаемый вид решения в уравнение
,
одна из которых зависит только от x, а
другая от t.
Тогда, подставив
предполагаемый вид решения в уравнение
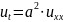 наше
решение
наше
решение
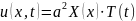 ,
получим:
,
получим:
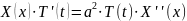
Поделим
обе части этого уравнения на
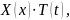 получим
получим
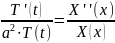
Видим, что в данном равенстве левая часть зависит только от t, а правая только от x. Функции разных переменных могут быть равны между собой только тогда, когда они равны константе.
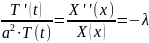
Получим два уравнения:
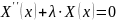
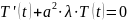
Рассмотрим первое уравнение
Нам
необходимо найти нетривиальные решения,
которые будут удовлетворять граничным
условиям:
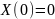 и
и
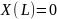 .
Для этого запишем и решим задачу
Штурма-Лиувилля:
.
Для этого запишем и решим задачу
Штурма-Лиувилля:
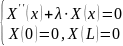
Характеристическое уравнение исходного дифференциального уравнения:
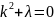
имеет
мнимые корни
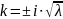
Следовательно, общее решение исходного дифференциального уравнения:
Для
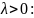
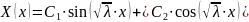
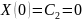 отсюда
следует, что
отсюда
следует, что
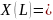 отсюда
отсюда
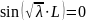 →
→
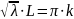
Получаем бесконечное множество собственных чисел:
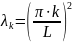
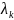 соответствует
бесконечное множество собственных
функций:
соответствует
бесконечное множество собственных
функций:
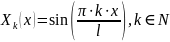
Для
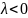 и для
и для
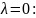 решений нет.
решений нет.
Получим,
что только для значений параметра
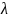 ,
равных
,
равных
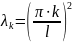
существуют нетривиальные решения уравнения , равные
Этим
значения
соответствуют решения уравнения
→
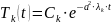 ,
где Сk – неопределенные пока
коэффициенты.
,
где Сk – неопределенные пока
коэффициенты.
Таким образом,
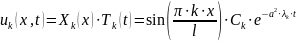
В
самом простом случае, например, когда
граничные функции
 и
и
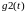 равны нулю и нет внешних источников
тепла, то есть
равны нулю и нет внешних источников
тепла, то есть
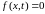 ,
аналитическое решение задачи может
быть найдено методом разделения
переменных и представляет собой ряд
Фурье:
,
аналитическое решение задачи может
быть найдено методом разделения
переменных и представляет собой ряд
Фурье:
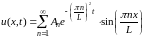 ,
(10.2) где
,
(10.2) где
 - коэффициенты ряда Фурье. Функции
- коэффициенты ряда Фурье. Функции
 являются
собственными функциями первой краевой
задачи. Еще их называют гармониками
ряда Фурье.
являются
собственными функциями первой краевой
задачи. Еще их называют гармониками
ряда Фурье.
Заметим,
что если функция
является
p-ой
гармоникой ряда (10.2), то
в силу ортогональности системы синусов
коэффициенты
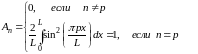
Тогда решение задачи будет представляться не бесконечным рядом, а функцией вида:
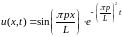 .
Это свойство будет использовано при
построении тестовых примеров. Физический
смысл такого решения означает, что в
отсутствии источников тепла
и
при постоянной нулевой температуре в
концах отрезка
.
Это свойство будет использовано при
построении тестовых примеров. Физический
смысл такого решения означает, что в
отсутствии источников тепла
и
при постоянной нулевой температуре в
концах отрезка
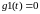 и
и
 значение температуры в стержне будет
стремиться к нулю .
значение температуры в стержне будет
стремиться к нулю .
Пример 10.1 Найти аналитическое решение задачи:
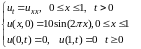
Решение.
Уравнение теплопроводности является
однородным, граничные условия первого
рода заданы нулевыми граничными
функциями, начальная температура
представляет собой 2-ую гармонику ряда
Фурье, умноженную на константу 10. Длина
стержня L=1.
Следовательно, решение задачи имеет
вид:
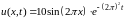 .
Построим профили температуры – графики
решения функции
.
Построим профили температуры – графики
решения функции
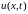 в
фиксированные моменты времени.
Возьмем
в
фиксированные моменты времени.
Возьмем
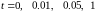 :
:
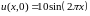 ,
,
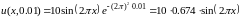
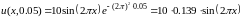 ,
,
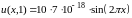
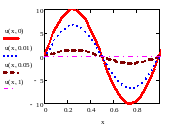
Видно, что при t=1 первоначальная температура стержня стала практически нулевой. Нулевая температура границ стержня охладила и весь стержень до нуля.
§ 10.2 Сетки, сеточные функции и разностные операторы
Введем
на отрезке [0,L]
пространственную сетку
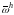 состоящую
из
точек
состоящую
из
точек
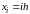 ,i=0..n
где
,i=0..n
где
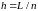 а
на
отрезке
[0,
T
]
временну´ю
сетку
а
на
отрезке
[0,
T
]
временну´ю
сетку
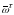 ,
состоящую
из
точек
,
состоящую
из
точек
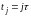 ,
j=0..m
где
τ
=
T/m.
Будем
также
использовать
множество
внутренних
узлов
,
j=0..m
где
τ
=
T/m.
Будем
также
использовать
множество
внутренних
узлов
 .
Внутренними
узлами
временн´ой
сетки
будем
называть
.
Внутренними
узлами
временн´ой
сетки
будем
называть
множество точек
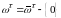 .
.
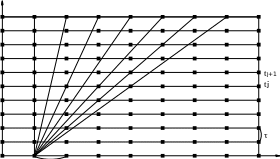
Множество точек
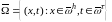 называется
пространственно-временн´ой
сеткой (на
рис.
1.1
обозначены
кружками).
Введем
также
множество
внутренних
точек
называется
пространственно-временн´ой
сеткой (на
рис.
1.1
обозначены
кружками).
Введем
также
множество
внутренних
точек
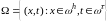 ,
которое
в
дальнейшем будет
играть
очень важную
роль.
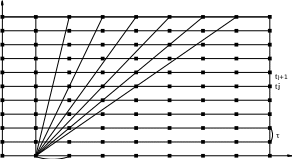
На рис. 12.1 представлена пространственно-временная
сетка.
,
которое
в
дальнейшем будет
играть
очень важную
роль.
На рис. 12.1 представлена пространственно-временная
сетка.
 t
T
t
T
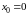
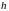
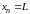
Рис 10.1
Будем называть временным слоем множество всех узлов сетки, имеющих одну и ту же временную координату. Так, j-м слоем будем называть точки:
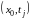 ,
,
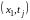 ,
,
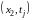 ,
…
,
…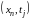
Для
функции, являющейся приближенным
значением к точному решению задачи -
функции u(x,t),
введем обозначение:
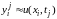 .Таким
образом, приближенное решение задачи
будет представлять собой матрицу
приближенных значений, заданных
.Таким
образом, приближенное решение задачи
будет представлять собой матрицу
приближенных значений, заданных
на
множестве
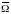 .
.
Для построения разностной схемы будем использовать метод конечных разностей.
Суть метода в том, что все разностные производные будем заменять разностными аналогами. Заменим производную по t правой разностной производной, а вторую производную по х известным нам уже равенством :
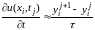 ,
,
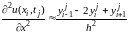
Отметим, что производная по t аппроксимирована с первым порядком точности по τ , а вторая производная аппроксимирована со вторым порядком точности по h. Следовательно, построенная схема будет иметь первый порядок аппроксимации по t и второй по h. При этом мы использовали следующий трехточечный шаблон:
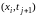

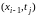
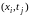
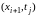
Запишем
разностное уравнение, аппроксимирующее
исходное дифференциальное уравнение:
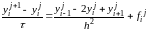 ,
i=1…n-1,
j=0…m-1
,
i=1…n-1,
j=0…m-1
Здесь
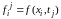 .
Индексы i
и j
взяты таким образом, чтобы разностное
уравнение
.
Индексы i
и j
взяты таким образом, чтобы разностное
уравнение
было
определено во всех внутренних узлах
сетки. Дополним разностные уравнения
значениями на нулевом слое (начальная
температура)
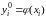 ,
i=0…n
и в граничных точках (граничные условия):
в левой точке
,
i=0…n
и в граничных точках (граничные условия):
в левой точке
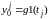 ,
j=0…m
и в правой точке
,
j=0…m
и в правой точке
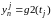 ,
j=0…m.
Окончательно получили систему равенств
для нахождения приближенного решения
задачи (12.1):
,
j=0…m.
Окончательно получили систему равенств
для нахождения приближенного решения
задачи (12.1):
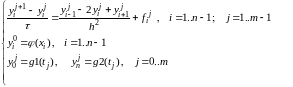 (10. 3)
(10. 3)
Система (10.3 ) называется явной разностной схемой для уравнения теплопроводности. Нахождение решения разностной схемы происходит по слоям: сначала задается решение на нулевом слое, затем задается решение в граничных точках справа и слева, и после этого приступаем к нахождению решения во внутренних точках.







Рассмотрим пример построения разностной схемы и нахождение приближенного решения следующей задачи :
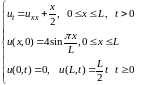
Зафиксируем
значения
 ,
выберем шаги по пространству и по
времени:
,
выберем шаги по пространству и по
времени:
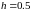 ,
,
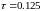 .
Правильный выбор параметров сетки
обсудим в следующей лекции. Тогда отрезок
.
Правильный выбор параметров сетки
обсудим в следующей лекции. Тогда отрезок
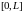 будет
разбит на 4 части точками:
будет
разбит на 4 части точками:
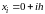 ,
,
 .
.
Прежде чем начать расчет по формулам вычисления приближенного решения подготовим таблицу, соответствующую пространственно-временной сетке и заполним ее известными значениями начальной температуры на нулевом слое и в граничных точках:
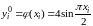 ,
,
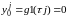
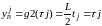
-
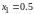
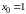
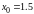
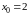
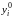
0
2.8284
4
2.8284
0
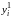
0
0.125
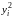
0
0.25
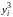
0
0.375
…..
……..
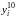
0
1.25
Преобразуем разностное уравнение так: выразим неизвестное значение на слое j+1
через
предыдущие значения:
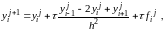
Для
упрощения расчетов введем параметр
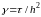 и соберем слагаемые с одинаковыми
индексами. Тогда формула для расчетов
примет такой вид:
и соберем слагаемые с одинаковыми
индексами. Тогда формула для расчетов
примет такой вид:
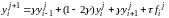 ,
,
При
выбранных значениях шагов по пространству
и по времени параметр
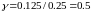 ,
а коэффициент
,
а коэффициент
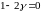 .
Начнем расчет первого слоя по времени
с точки
.
Начнем расчет первого слоя по времени
с точки
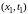 :
: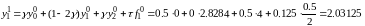 Считаем
температуру в точке
Считаем
температуру в точке
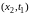 :
:
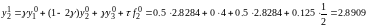 Последняя
внутренняя точка первого слоя
Последняя
внутренняя точка первого слоя
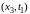
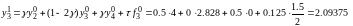
Таким образом, 1-ый слой по времени найден, и аналогично можно заполнить вторую строку таблицы. Для нахождения 2-го временного слоя действуем аналогично. Продвигаясь снизу вверх и слева направо, можно вычислить значения температуры стержня при любом значении T. ( В таблице представлены числа с 4 знаками после запятой)
-
0
2.8284
4
2.8284
0
0
2.03125
2.8909
2.09375
0.125
0
1.4767
2.125
1.6017
0.25
0
1.0938
1.6017
1.2813
0.375
…
….
…
…

0
0.4009
0.75
1.0259
1.25
В предпоследней строке таблицы приведены значения температуры на 10 временном слое.
Графики приближенного решения задачи (профили температуры) приведены ниже.
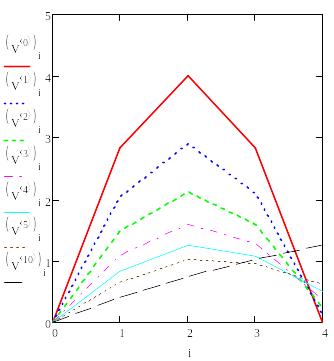
На
графиках через
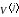 обозначены
профили температуры на j-слое
по времени.
обозначены
профили температуры на j-слое
по времени.
Для
сравнения поработаем с аналитическим
решением. Легко проверить, что функция
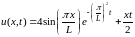 является
аналитическим решением задачи.
является
аналитическим решением задачи.
Заполним таблицу со значениями аналитического решения по слоям:
-
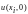
0
2.8284
4
2.8284
0
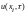
0
2.1090
3.000
2.1715
0.125
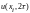
0
1.5888
2.2835
1.7138
0.25
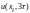
0
1.2150
1.7732
1.4025
0.375
….
….
….
…..
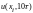
0
0.4419
0.8080
1.0669
1.25
Сравнивая полученные решения, имеем: приближенное решение:
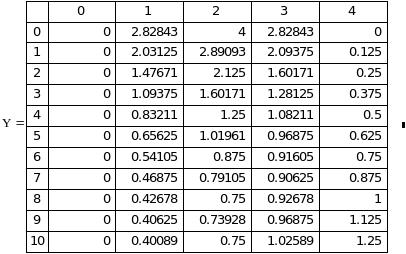
Аналитическое решение:
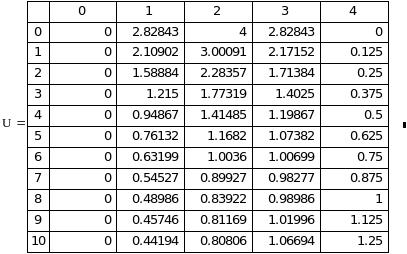
Оба
решения найдены по программе. Оценим
норму вектора погрешности на 10-м слое
по времени:
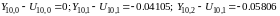 ,
,
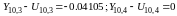
Тогда
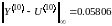
Явная
разностная схема имеет существенный
недостаток: она является условно-устойчивой,
то есть она сходится при определенном
соотношении шагов
 и h,
а именно,
и h,
а именно,
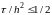 .
Это означает, что вычисления должны
идти с очень мелким шагом по времени. В
следующей лекции будет рассмотрена
абсолютно устойчивая схема, которая
свободна от этого недостатка.
.
Это означает, что вычисления должны
идти с очень мелким шагом по времени. В
следующей лекции будет рассмотрена
абсолютно устойчивая схема, которая
свободна от этого недостатка.