
ЛЕКЦИЯ 5. РЕШЕНИЕ ЗАДАЧИ КОШИ.
ЛИТЕРАТУРА. Учебник [1] Глава 14. §14.2,14.7
§ 5.1 Построение методов на основе квадратурных формул.
Рассмотрим задачу Коши.
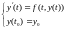 при
при
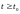 (5.1)
(5.1)
Проинтегрируем
уравнение на отрезке
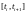 :
:
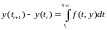
Вычислить интеграл, стоящий в правой части невозможно, так как функция f(t,y) содержит неизвестную функцию y(t). Для вычисления интеграла воспользуемся квадратурными формулами.
1. Применим формулу левых прямоугольников:
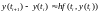
Или:
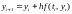
Получили метод Эйлера. Перепишем его в каноническом виде:
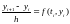
Метод
1-го порядка точности по h.
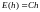
2. Применим метод центральных прямоугольников:
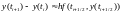
Так как значение
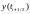 неизвестно, то для его нахождения
выполним полшага методом Эйлера:
неизвестно, то для его нахождения
выполним полшага методом Эйлера:
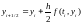
Тогда расчетная формула примет вид:
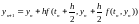
Получили расчетную формулу усовершенствованного метода Эйлера.
В канонической форме метод примет вид:
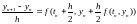
Получили
метод 2-го порядка точности по h
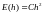 .
.
3. Применим формулу правых прямоугольников:
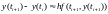
Или:
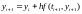
Получили
неявный
метод Эйлера.
В правую часть уравнения входит
неизвестное значение
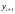 .
.
Перепишем его в каноническом виде:
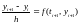
Метод 1-го порядка точности по h.
4. Применяя метод трапеций можно получить метод Эйлера-Коши или правило трапеций.

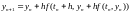
Метод 2-го порядка
точности по h.
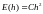 .
.
Можно получить также классический метод Рунге-Кутты 4-го порядка точности, применяя формулу Симпсона:
![]()
Для вычисления неизвестных значений
![]() ,
,
![]()
Выполним следующее:
![]() ,
,
Затем, используя это значение, вычислим:
![]()
![]()
![]()
Тогда формула Симпсона примет вид:
![]()
Получили
метод 4-го порядка точности по h
![]()
Рассмотрим как можно реализовать неявный метод Эйлера.
ПРИМЕР 5.1.Дана задача Коши:
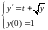 Найти решение
задачи в двух последующих точках 0.1 и
0.2.
Найти решение
задачи в двух последующих точках 0.1 и
0.2.
Выберем шаг h=0.1 и запишем расчетные формулы неявного метода Эйлера:
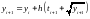
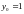
Можно реализовать алгоритм в виде прогноза-коррекции:
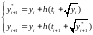 прогноз делаем
по явному методу Эйлера, коррекцию –
по
прогноз делаем
по явному методу Эйлера, коррекцию –
по
неявному методу.
Расчеты:
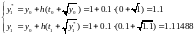
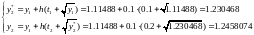
ОТВЕТ:
,
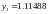 ,
,
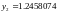
§5.2. Определения погрешностей. Аппроксимация и сходимость
ЧИСЛЕННОГО МЕТОДА.
Запишем метод Эйлера и метод Тейлора в т.н. канонической форме:
Метод Эйлера:
Метод Тейлора:
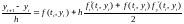
Можно считать, что левая часть методов представляет собой аппроксимацию производной, правая часть – аппроксимацию правой части уравнения задачи Коши.
Заметим, что оба метода являются явными одношаговыми методами. В более общей
форме будем записывать явные одношаговые методы так:
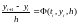 (5.1)
(5.1)
Далее будем изучать более сложные методы: явные k-шаговые и неявные k-шаговые методы.
Для k-
шагового метода будем считать, что
известны значения
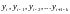
Тогда каноническая форма явного k-шагового метода примет вид:
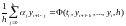 (5.2)
(5.2)
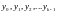 известны.
известны.
Каноническая форма неявного k-шагового метода имеет вид:
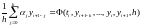 (5.3)
(5.3)
известны.
Выражение (5.3)
отличается от (5.2) тем, что и в левую,
и в правую части входит неизвестное
значение
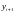 .
.
ОПР. Будем называть задачу (5.3) k -шаговым неявным разностным методом или дискретной задачей Коши в канонической форме.
ОПР. Будем называть
погрешностью сеточную функцию
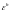 со значениями в узлах
со значениями в узлах
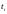 равными
равными
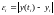
Напомним, что
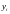 -
приближенное решение задачи, а
-
приближенное решение задачи, а
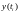 - точное решение задачи в точке
.
- точное решение задачи в точке
.
ОПР. В качестве
меры погрешности метода примем величину
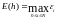
называемую глобальной погрешностью.
ОПР. Будем
говорить, что метод сходится с p-ым
порядком точности по h,
если справедливо неравенство:
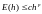 ,
где c
– константа,
не зависящая от h.
,
где c
– константа,
не зависящая от h.
ОПР. Пусть
y(t)
– решение задачи Коши. Назовем сеточную
функцию
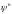 ,
определяемую
,
определяемую
формулой
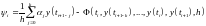 (5.4)
(5.4)
Погрешностью аппроксимации на решении y(t).
Замечание. Из определения следует, что функция y(t) удовлетворяет уравнению (5.4) с
точностью до погрешности аппроксимации.
Сеточную функцию используют для предварительной оценки того, насколько точно
аппроксимируется дифференциальное уравнение сеточным аналогом.
ОПР. Говорят,
что разностное уравнение аппроксимирует
исходное дифференциальное уравнение
с p-ым
порядком, если
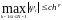 ,
p>0
,
p>0
ПРИМЕР. Найдем погрешность аппроксимации метода Эйлера.
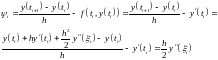
Теперь оценим
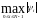 . Обозначим
через
. Обозначим
через
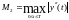 .
Тогда
очевидно, что
.
Тогда
очевидно, что
справедлива оценка
:
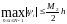 .
Таким образом,
метод Эйлера
имеет первый порядок аппроксимации по
h.
.
Таким образом,
метод Эйлера
имеет первый порядок аппроксимации по
h.
