Все за 2й курс / Лекция 4

ЛЕКЦИЯ 4. Решение нелинейных уравнений

ЛИТЕРАТУРА. Учебник [1] §4.4. §4.7, §4.2.

§4.1. Метод простой итерации с параметром

Дано нелинейное уравнение:

(4.1)

Уравнение (4.1) преобразуется к виду , который называется видом, удобным для итераций, а функция — итерационной функцией. Далее задается начальное приближение и строится последовательность приближений к корню по формуле

(4.2)

На прошлой лекции была доказана теорема.

Теорема 3.2. Если в окрестности корня функция непрерывно дифференцируема и удовлетворяет условию

, (3.10)

то метод простой итерации сходится и справедливы априорная оценка погрешности

(3.11)

означающая, что метод сходится со скоростью геометрической прогрессии со знаменателем , и апостериорная оценка погрешности

(3.12)

из которой для заданной точности следует критерий окончания итераций

(3.13)

В этом случае является искомым приближением с точностью .

Не всегда возможно простым преобразованием уравнения найти итерационную функцию,

удовлетворяющую условию (3.10). Однако есть способ, при котором гарантированно выполнено это условие.

Метод простой итерации с параметром.

В этом способе приведения к виду, удобному для итераций, итерационная функция имеет вид

(4.3)

где — параметр, выбираемый таким образом, чтобы величина была минимальной. Тогда метод (4.3) будет сходиться максимально быстро, т.е. для достижения заданной точности требуется минимальное количество итераций.

Если в окрестности корня функция 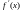строго знакопостоянна, например,

выполняется условие 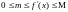_, то оптимальное значение параметра находится по формуле

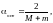(4.4)

при этом метод сходится со скоростью геометрической прогрессии со знаменателем

Поскольку для нахождения каждого корня необходимо вычислить лишь величины и , преобразование (4.3) называют универсальным.

ПРИМЕР 4.1. Найти корень уравнения на отрезке методом простой итерации с точностью .

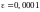Решение. Воспользуемся параметрической формой метода простой итерации. В данной задаче можно воспользоваться этим методом, так как производная функции строго положительна и на заданном отрезке монотонно возрастает. Следовательно,

По формуле (2.6) получаем значение оптимального параметра

и тогда . Также находим знаменатель сходимости метода

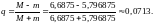
Возьмем в качестве начального приближения середину отрезка локализации: . Вычисляем

и проверяем критерий окончания итераций

В нашем случае имеем

Выполняем следующую итерацию

и проверяем критерий окончания итераций: . На этот раз неравенство верное, а значит итерации можно прекратить. В соответствии с погрешностью ответ записываем с четырьмя знаками после запятой.

Ответ. .

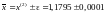Пояснение выбора параметра.

_{Рассмотрим итерационную функцию и попробуем выбрать параметр, исходя из достаточного условия сходимости (3.10).}

_{Найдем производную: и решим неравенство: . Тогда:}

_или

_{Это означает, что знак параметра должен совпадать со знаком производной. Мы предположили, что производная знакопостоянна и выполнено неравенство:}

_{Тогда параметр можно выбирать из интервала: .}

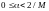_{В случае, когда производная отрицательна, можно умножить исходное уравнение на -1 и функция из убывающей превратится в возрастающую, то есть знак производной будет положительным.}

Порядок (скорость) сходимости. Пусть в некоторой окрестности (вообще говоря, малой) корня уравнения (2.1) итерационная последовательность удовлетворяет неравенству

_где — постоянная и . Тогда называется порядком сходимости метода.

_{Метод простой итерации с параметром является линейно сходящимся методом, то есть p=1}

§4.2. Модификации метода Ньютона.

Упрощенный метод Ньютона. В этой модификации метода Ньютона производная функции вычисляется только один раз — в начальном приближении . Расчетная формула имеет вид

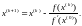(4.5)

Упрощённый метод Ньютона представляет собой метод простой итерации с итерационной функцией

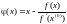
и обладает линейной сходимостью. Для достижения заданной точности требуется тем меньше итераций, чем ближе к корню лежит точка .

Метод ложного положения. Метод основан на следующей аппроксимации производной

(4.6)

где — некоторая точка из окрестности корня. Расчетная формула:

Метод ложного положения представляет собой метод простой итерации с итерационной функцией

(4.7)

и обладает линейной сходимостью. Для достижения заданной точности требуется тем меньше итераций, чем ближе к корню лежит точка .

Метод секущих. Метод основан на следующей аппроксимации производной

(4.8)

Расчетная формула метода

Метод имеет порядок сходимости , т.е. обладает сверхлинейной сходимостью.

Метод Стеффенсена. Идея аппроксимации производной основана на малости значения в малой окрестности корня. Поэтому берется в качестве приращения аргумента:

(4.9)

Расчетная формула метода

Метод имеет второй порядок сходимости, т.е. обладает квадратичной сходимостью.

Модификация метода Ньютона для кратных корней. Если искомый корень имеет кратность , то классический метод Ньютона из п.8 сходится к нему лишь линейно (со скоростью геометрической прогрессии со знаменателем ). Однако метод

(4.10)

обладает квадратичной сходимостью в окрестности такого корня.

§4.3. Интервал неопределенности корня.

Пусть между абсолютными погрешностями входных данных x и решения y

_{установлено неравенство}: _{.Тогда величина - называется}

_{абсолютным числом обусловленности. Если выполнено неравенство для относительных погрешностей:}

_{То число называется относительным числом обусловленности.}

_{Если число достаточно велико, то задача называется плохо обусловленной.}

При вычислениях на компьютере значения функции вычисляются с погрешностью: , причём предположим, что в окрестности корня . Это приводит к тому, что существует такая окрестность корня 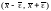, что при попадании в нее итерационной последовательности невозможно определить, какая точка представляет собой корень уравнения (2.1). Эта окрестность называется интервалом неопределенности. Внутри этого интервала любую точку можно принять за роиближение к корню. Найдем оценку радиуса интервала неопределенности корня.

Отсюда можно написать приближенное равенство:

Взяв модуль и, используя понятии абсолютной погрешности, имеем:

Если корень простой, то радиус интервала неопределенности оценивается по формуле

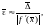(4.11)

а если имеет кратность , то по формуле

Поскольку значение корня на практике неизвестно, то вместо него можно взять любую достаточно близкую к нему точку.

Также величина заведомо не превышает величины, примерно равной , так как внутри такой окрестности может не оказаться чисел, представимых на компьютере, кроме одного (близкого или равного ).