Алгоритм Косарайю (S.R.Kosaraju) нахождения ССК орграфа
(на основе двух ПВГ)
1.Выполнить ПВГ орграфа G и вычислить номера вершин в порядке их использования fn[*].
2.Сконструировать новый (обращенный) орграф GR , путем обращения всех дуг исходного графа.
3.Выполнить ПВГ орграфа GR , начиная с вершины, имеющей наибольший номер fn[ ]. Если ПВГ не завершен, то продолжить, начиная с вершины, имеющей наибольший номер fn[ ] среди оставшихся.
4.Каждое дерево полученного глубинного остовного дерева (леса) орграфа GR является ССК орграфа G.
28.04.2014 |
Сильно связные компоненты |
30 |
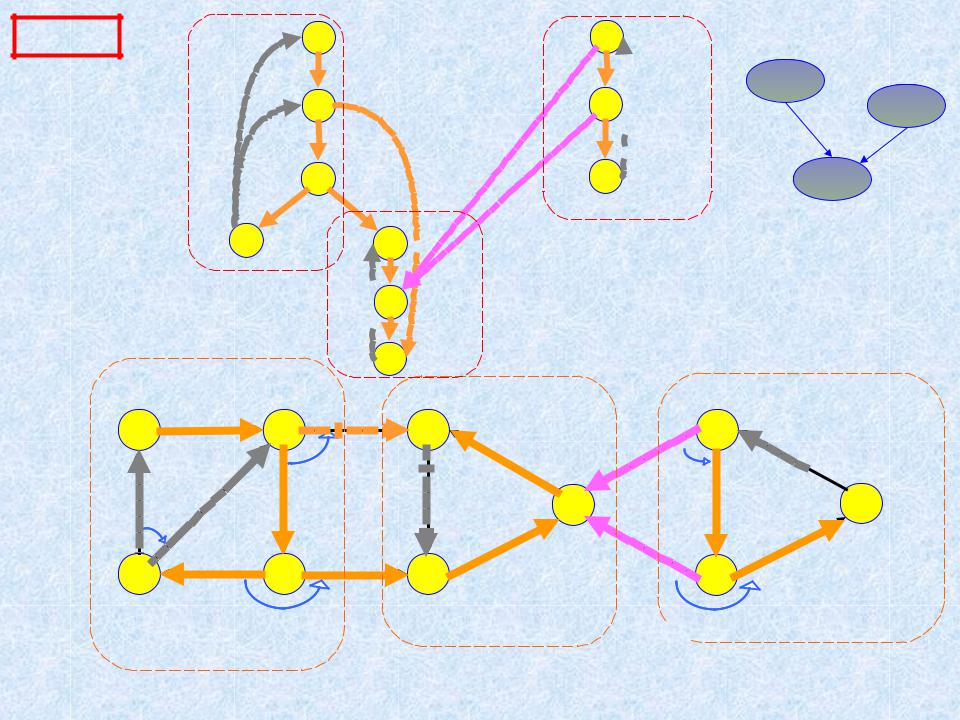
копия |
1 |
a |
(7) |
8 |
h |
(10) |
|
|
|
b |
(6) |
9 |
i |
(9) |
abde |
|
2 |
hij |
|||||
|
3 |
e |
(5) |
10 |
j |
(8) |
cfg |
|
4 |
d (1) 5 |
f (4) |
||
|
|
|
6 |
g |
(3) |
|
|
|
7 |
c |
(2) |
|
|
|
|
||
1 |
(7) |
2 |
(6) |
7 |
(2) |
|
a |
|
|
c |
|
|
|
|
|
|
g |
|
d |
|
|
f |
6 (3) |
4(1) |
3 (5) |
5 (4) |
|||
8 |
(10) |
|
h |
j 10
(8)
(9)
9
28.04.2014 |
Сильно связные компоненты |
31 |
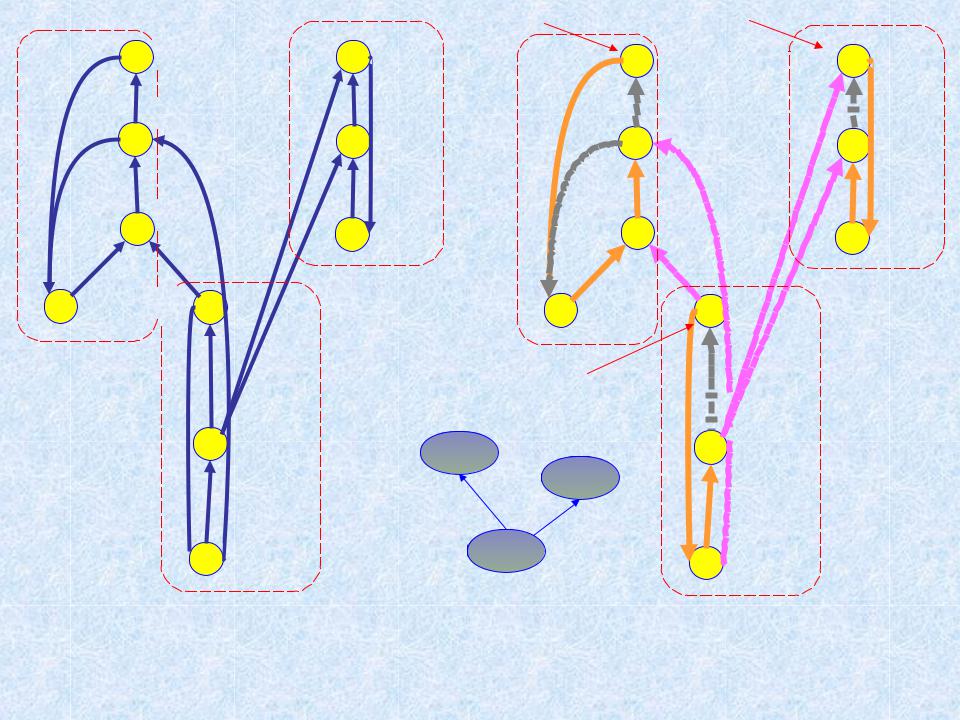
a 
(7)
b 
(6)
e 
(5)
d (1) 
f
(4)
g (3)
c (2)
Обращенный граф
|
(10) |
II |
(7) |
I |
(10) |
h |
a |
|
h |
||
i |
(9) |
b |
|
|
i |
j |
(8) |
e |
j |
|
|
|
(4) |
|
|
d |
f |
|
|
III |
|
|
|
abde |
g |
|
|
hij |
|
|
|
cfg |
c |
|
|
|
ПВГ в обращенном графе
28.04.2014 |
Сильно связные компоненты |
32 |
Основные факты (утверждения), на которые опирается доказательство
правильности алгоритма
1.Граф ССК GССК орграфа G – ациклический
2.ССК орграфов G и GR совпадают (как множества вершин)
3.При втором ПВГ граф ССК (GR)ССК орграфа GR проходится в порядке, обратном топологической сортировке
28.04.2014 |
Сильно связные компоненты |
33 |
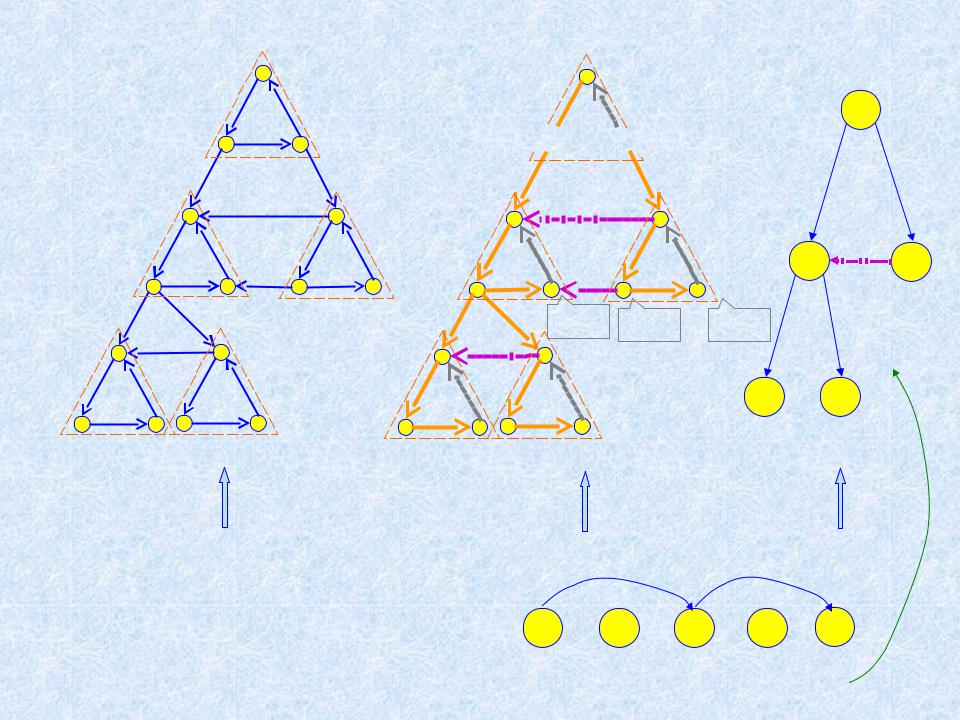
Пример (пояснение к утверждениям)
1/15
2/14
3/9
A
12/13
13/12
|
4/8 |
|
B |
C |
|
|
|
|
|
5/3 |
11/7 |
14/11 |
15/10 |
|
8/6 |
|
|
|
|
|
|
|
|
D 
E
6/2
7/1 9/5 10/4
G |
ПВГ в G |
GССК |
A 
C 
B 
E 
D
28.04.2014 |
Сильно связные компоненты |
Топ. сорт. графа |
35 |
|
|
|
|
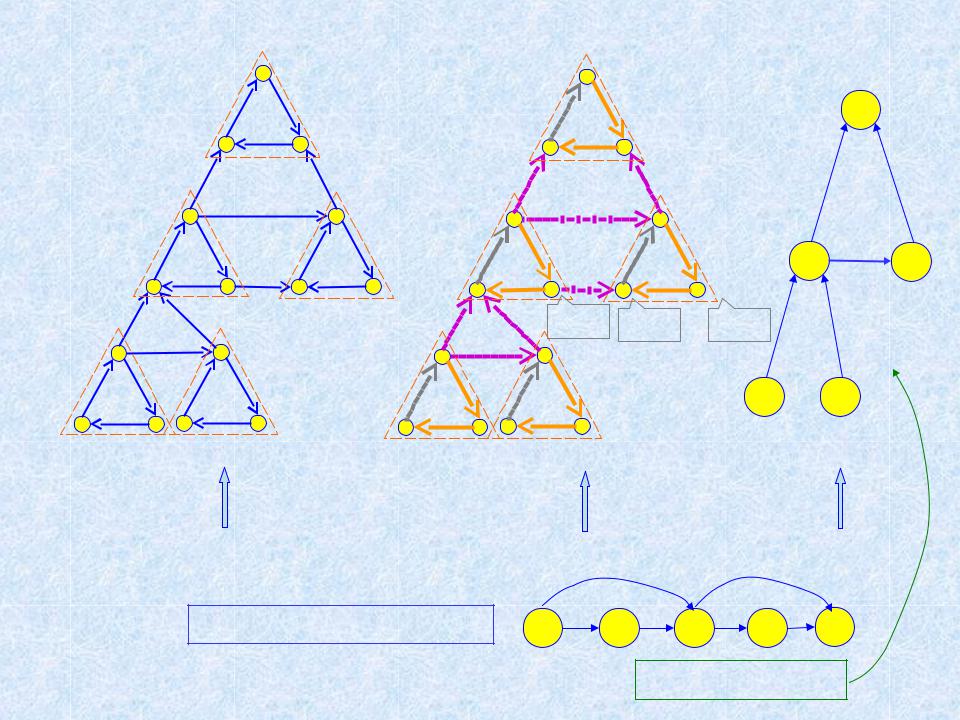
Пример (продолжение)
1-15
|
|
|
|
A |
|
3-14 |
2-13 |
|
|
|
7-9 |
|
4-12 |
|
9-8 |
|
|
B |
C |
|
|
|
|
|
13-3 |
8-7 |
6-11 |
5-10 |
|
10-6 |
|
|
|
|
|
|
|
|
|
D 
E
15-2
14-1 12-5 11-4
GR |
|
ПВГ в GR |
(GR)ССК |
||
A C B E D |
D |
E |
B C A |
|
|
28.04.2014 |
Сильно связные компоненты |
|
Топ. сорт. графа |
36 |
|
Сложность алгоритмов нахождения ССК
Алгоритм Тарьяна (Tarjan R.E.) Алгоритм Косарайю (S.R.Kosaraju)
O (n +m)
КОНЕЦ ССК
28.04.2014 |
Сильно связные компоненты |
37 |
КОНЕЦ ЛЕКЦИИ
КОНЕЦ ЛЕКЦИИ
КОНЕЦ ЛЕКЦИИ
КОНЕЦ ЛЕКЦИИ
КОНЕЦ ЛЕКЦИИ
КОНЕЦ ЛЕКЦИИ
КОНЕЦ ЛЕКЦИИ
КОНЕЦ ЛЕКЦИИ