Методы / Tdu_4

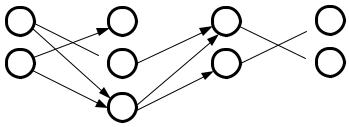
1.3.3.Алгоритм минимизации таблиц переходов

ипоследовательность его шагов

Будем рассматривать алгоритм, иллюстрируя каждый его шаг на примере минимизации табл. 2.

Шаг 1. Нахождение множеств совместимых по столбцу строк

Для реализации данного пункта алгоритма находятся множества Eij –

множества строк, в которых в столбце j указано состояние i или знак безразличного состояния «~». Если в столбце есть только одно устойчивое состоя-

ние, то множество Eij не составляется. В соответствии с этим правилом выписаны подмножества совместимых по столбцам строк:

четверок чисел i1, i2, i3, i4. На рис. 7 показан принцип пересечения множеств Eij . В итоге получается 2 · 3 · 2 · 2 = 24 множества.

E11 E42 E23 E34

E81 E52 E73 E64

E92

Рис. 7. Схема образования множеств Ei1 ,i2 ,i3 ,i4

Приведем множества Ei1 ,i2 ,i3 ,i4 , полученные из множеств Eij первого шага. Для примера образования Ei1 ,i2 ,i3 ,i4 рассмотрим пересечение множеств столбцов E11 , E42 , E23 , E34 :

E1,4,2,3 E11 E42 E23 E34 1,3, 4,5, 6, 7,9 2,3, 4, 6, 71, 2,3, 4,5,8,9 1, 2,3, 4, 7,8,9 3, 4 .

10

Другими словами, находятся числа, присутствующие во всех множествах Eij . Если при пересечении множеств Eij не находится одинаковых

чисел, то ставится знак « » – пустое множество. В виде списка приведем все 24 пересечения:

Шаг 3. Выбор максимальных подмножеств совместимых строк

Из полученных на втором шаге множеств пересечений Ei1,i2 ,i3 ,i4 ис-

ключаются все те, которые полностью входят в другие подмножества (пустые множества входят в любые множества, а из одинаковых множеств выбирается любое). Оставшиеся множества являются искомыми Emax, они обозначаются большими латинскими буквами:

Шаг 4. Составление таблицы покрытий

Таблица покрытий представляет собой таблицу, в которой по строкам располагаются состояния многотактной схемы (строки таблицы переходов), а по столбцам – Emax. В нашем случае это таблица размером 9×8. На пересечении строки и столбца ставится знак покрытия (произвольная метка, к примеру, «+»), если номер данной строки входит в соответствующее Emax. Заполненная для рассматриваемого примера таблица покрытий представлена ниже (табл. 4).

11

Таблица 4

Таблица покрытий

Шаг 5. Решение задачи покрытия

Находится минимальное множество столбцов – такое, что каждая строка имеет метку хотя бы в одном столбце. Для этого составляется алгебраическое выражение, представляющее собой конъюнкцию дизъюнкций тех столбцов, в которых стоит знак покрытия «+». Число конъюнкций равно числу строк. Обращаясь к табл. 4, получаем:

Скобки раскрываются и выражение (1) приводится к дизъюнктивной форме – выражению без скобок, содержащему дизъюнкции конъюнкций. В преобразованиях используют известные законы алгебры логики [1, 2].

Закон повторения:

где φ – любое логическое выражение.

Используя выражение (4), упростим формулу (1). При этом удалим

12

Далее следует раскрыть скобки. Здесь полезной может оказаться такая формула:

При раскрытии скобок сгруппируем такие члены: F G G H иA F A B . К ним применима формула (6).

Приведем оставшиеся преобразования по получению дизъюнктивной формы выражения:

Шаг 6. Выбор оптимального варианта совмещения строк

Из последнего выражения в дизъюнктивной нормальной форме выбирается любая конъюнкция, содержащая минимальное число букв. Из формулы (7) видно, что это конъюнкция CEGA. Буквы в конъюнкции заменяются множествами Emax (см. шаг 3). Получаем:

В выражении (8) из любого подмножества произвольным образом исключаются повторяющиеся номера совмещаемых строк:

Отметим, что в формуле (9) после минимизации присутствуют все номера первичной таблицы переходов, повторяющихся номеров нет.

Шаг 7. Объединение строк первичной таблицы переходов

В § 1.3.1 рассмотрены принципы совмещения строк, приведем таблицу переходов (табл. 5), где выполнены объединения согласно выраже-

нию (9).

Таблица 5

Преобразованная таблица переходов

13

Шаг 8. Перенумерация строк минимизированной таблицы переходов

Для этого все номера в таблице из множества {1,5} заменяются на 1, {6,9} – на 2, {2,8} – на 3, {3,4,7} – на 4. Минимизированная таблица переходов – это представленная ниже табл. 6.

Таблица 6

Минимизированная таблица переходов

Итогом минимизации является сокращение числа строк первичной таблицы переходов до пяти. Для реализации многотактной схемы по табл. 6 потребуется на одну внутреннюю переменную меньше.

2.МЕТОДИКА ВЫПОЛНЕНИЯ РАБОТЫ

1.Ознакомиться с разделом 2 данных методических указаний.

2.Получить вариант у преподавателя.

3.По заданной вход-выходной последовательности построить временные диаграммы и первичную таблицу переходов.

4.Найти максимальные подмножества Emax совместимых строк первичной таблицы переходов.

5.Исключить максимальные подмножества Emax, полностью входящие в другие максимальные подмножества.

6.Составить таблицу покрытий.

7.По таблице покрытий получить дизъюнктивную нормальную форму записи, содержащую все возможные варианты минимизации.

8.Выбрать конъюнкцию с минимальным числом букв и поставить ей

всоответствие подмножества совместимых строк.

9.Объединить строки по рассмотренным в § 1.3.1 правилам.

10.Перенумеровать строки минимизированной таблицы переходов.

14

3. ВАРИАНТЫ ЗАДАНИЙ

15

16

17

18

4. ЗАДАНИЯ ПОВЫШЕННОЙ СЛОЖНОСТИ

Построить и минимизировать таблицу переходов по заданной временной вход-выходной диаграмме.

Библиографический список

1.Поспелов Д. А. Логические методы анализа и синтеза схем / Д. А. Поспелов. – Изд. 3-е, перераб. и доп. – М. : Энергия, 1974. – 368 с.

2.Сапожников В. В. Теория дискретных устройств железнодорожной автоматики, телемеханики и связи / Вал. В. Сапожников, Ю. А. Кравцов, Вл. В. Сапожников ; под ред. Вал. В. Сапожникова. – М. : УМК МПС Рос-

сии, 2001. – 312 с.

19