
- •М.А. Шварц
- •Конспект лекций
- •23.05.05 «Системы обеспечения движения поездов»
- •Раздел 9. Числовые и функциональные ряды. Гармонический анализ
- •Санкт-Петербург 2020
- •Числовые ряды
- •Достаточные признаки сходимости положительных рядов
- •Тема 13
- •Тема 14 Функциональные ряды. Равномерная сходимость
- •Степенные ряды
- •Тема 15 Ряды Тейлора и Маклорена
- •Ряды Маклорена основных функций
- •Применение степенных рядов в приближенных вычислениях
- •Тема 16 Тригонометрические ряды Фурье
- •Комплексная форма ряда Фурье
- •11.2 Контрольные тесты
Комплексная форма ряда Фурье
Применяя формулы
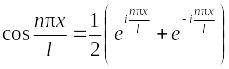 ,
,
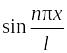
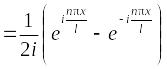 ,
,
можно представить ряд Фурье в комплексной форме
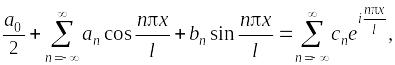
где
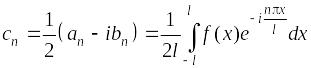 ,
п =
0, ±1,
±2,
±3,
...
,
п =
0, ±1,
±2,
±3,
...
Слагаемые
ряда Фурье представляют собой гармоники
с амплитудами
![]() и фазами
и фазами
![]() .
Частоты колебаний wn
образуют бесконечную арифметическую
прогрессию с разностью
.
Частоты колебаний wn
образуют бесконечную арифметическую
прогрессию с разностью
 .
Графически это отображается диаграммами
– амплитудным
.
Графически это отображается диаграммами
– амплитудным
![]() и фазовым
и фазовым
![]() спектрами. Взаимно однозначное
соответствие между заданной функцией
и ее спектрами позволяет получить два
возможных представления функции:
координатное f(x)
и спектральное – амплитудой An
и фазой jn.
спектрами. Взаимно однозначное
соответствие между заданной функцией
и ее спектрами позволяет получить два
возможных представления функции:
координатное f(x)
и спектральное – амплитудой An
и фазой jn.
Пример. Записать комплексный ряд Фурье для периодической функции, изображенной на рисунке 11.9. Изобразить амплитудный и фазовый спектры.

Рис. 11.9
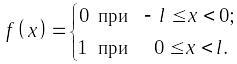
 ;
;
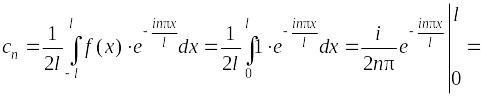
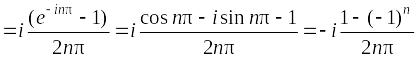 ,
,
![]() ;
;
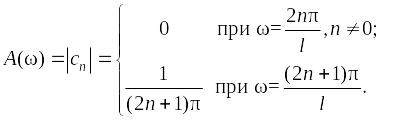
Амплитудный спектр представлен на рисунке 10.
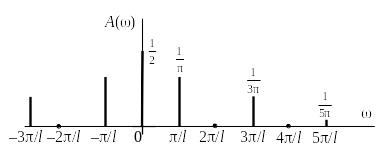
Рис. 10
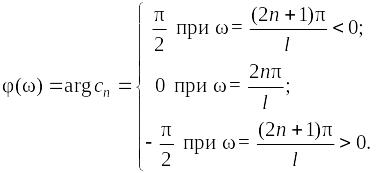
Фазовый спектр представлен на рисунке 11.

Рис. 11
11.2 Контрольные тесты
№ |
Задание |
Ответ |
||
1 |
Если
формула n-го
члена числовой последовательности
имеет вид
|
|
||
2 |
Необходимый
признак сходимости числового ряда
1)
|
|
||
3 |
Установите соответствие между рядами и их названиями.
1)
2)
3)
|
|
||
4 |
Числовой ряд
1) расходится 2) сходится 3) сходится условно 4) сходится абсолютно |
|
||
5 |
Если
1) 1,5 2) 0,2 3) 0,5 4) –2 |
|
||
6 |
Если
1) –1,5 2) 0,9 3) 0,5 4) 1 |
|
||
7 |
Числовой
ряд
1) расходится 2) сходится 3) сходится условно 4) сходится абсолютно |
|
||
8 |
Если
ряд
сходится и
1)
ряд
2) ряд сходится 3) ряд сходится условно 4) требуется дополнительное исследование сходимости ряда |
|
||
9 |
Радиус
сходимости степенного ряда
1) (– 9; 9) 2) (0; 9) 3) (– 9; 0) 4) (– 4,5; 4,5) |
|
||
10 |
Для сходимости ряда Тейлора к функции f(x) на некотором интервале необходимо и достаточно, чтобы для всех x на этом интервале для остаточного члена формулы Тейлора выполнялось условие
1)
|
|
||
11 |
Область
сходимости ряда
1) [–1; 1] 2) (–1; 1) 3) (0; 1) 4) [0; 1] |
|
||
12 |
Ряд имеет область сходимости
1) (–1; 1) 2) [–1; 1] 3) (–1; ¥) 4) (–¥; ¥) |
|
||
13 |
Для функции f(x) периода Т = 2l не выполняются условия Дирихле, если f(x) на отрезке [–l; l]
1) непрерывна 2) имеет конечное число разрывов первого рода 3) имеет конечное число разрывов второго рода 4) монотонна |
|
||
14 |
График нечетной периодической функции изображен на рисунке
1)
3)
|
|
||
15 |
1)
3)
|
|
||
16 |
Ряд
Фурье для функции
1) 2) 3) 4) |
|

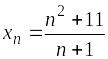
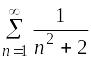 A)
знакочередующийся
A)
знакочередующийся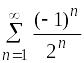 B)
степенной.
B)
степенной.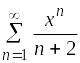 С)
с неотрицательными членами
С)
с неотрицательными членами
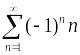
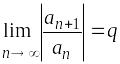 ,
то ряд сходится при q,
равном
,
то ряд сходится при q,
равном
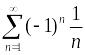

 равен 9. Тогда интервал сходимости
имеет вид…
равен 9. Тогда интервал сходимости
имеет вид…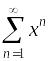 равна
равна 2)
2)

 4)
4)


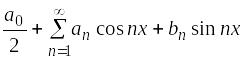 2)
2)
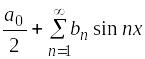
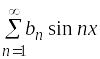 4)
4)
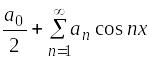
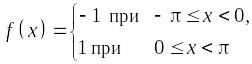 периода Т = 2p
имеет вид
периода Т = 2p
имеет вид