- •М.А. Шварц
- •Конспект лекций
- •23.05.05 «Системы обеспечения движения поездов»
- •Раздел 9. Числовые и функциональные ряды. Гармонический анализ
- •Санкт-Петербург 2020
- •Числовые ряды
- •Достаточные признаки сходимости положительных рядов
- •Тема 13
- •Тема 14 Функциональные ряды. Равномерная сходимость
- •Степенные ряды
- •Тема 15 Ряды Тейлора и Маклорена
- •Ряды Маклорена основных функций
- •Применение степенных рядов в приближенных вычислениях
- •Тема 16 Тригонометрические ряды Фурье
- •Комплексная форма ряда Фурье
- •11.2 Контрольные тесты
Тема 15 Ряды Тейлора и Маклорена
Пусть функция f(x) имеет производные любого порядка в точке х = а и некоторой ее окрестности. Рядом Тейлора функции f(x) называется степенной ряд
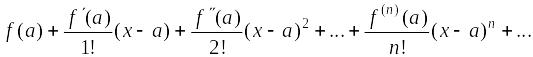
Ряд Тейлора может быть и расходящимся и сходящимся, причем в последнем случае возможно как S(x) = f(x), так и S(x) ¹ f(x).
Теорема.
Для сходимости ряда Тейлора к функции
f(x)
на некотором интервале необходимо и
достаточно, чтобы для всех x
на этом интервале остаточный член
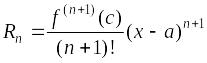 ,
сÎ(х; а)
формулы Тейлора функции f(x)
стремился к нулю (
,
сÎ(х; а)
формулы Тейлора функции f(x)
стремился к нулю (![]() )
при неограниченном возрастании n.
)
при неограниченном возрастании n.
При а = 0 ряд Тейлора принимает вид:
f(0)
+
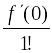 х
+
х
+
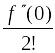 х2
+…+
х2
+…+ хn
+ …
хn
+ …
и называется рядом Маклорена.
Пример. Определить область сходимости ряда Тейлора для функции f(x) = е х в точке х = а.
Ряд
Тейлора функции f(x) = е
х: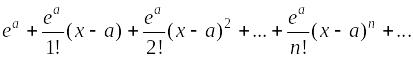


По признаку Даламбера ряда сходится при любых значениях х.
Пример.
Найти сумму ряда Маклорена
![]() .
.
При
![]() сумма бесконечно убывающей геометрической
прогрессии
сумма бесконечно убывающей геометрической
прогрессии
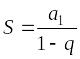 с знаменателем q = x
и а1 = 1
равна
с знаменателем q = x
и а1 = 1
равна
![]()
Пример. Разложить в ряд Маклорена функцию f(х) = sin х.
№ n |
f (n)(х) |
f (n)(0) |
|
0 |
f(х) = sinх |
|
0 |
1 |
f ¢(х) = cosх |
|
1/1! |
2 |
f ²(х) = –sinх |
|
0 |
3 |
f ¢²(х) = –cosх |
|
–1/3! |
4 |
f IV(х) = sinх |
|
0 |
Остаточный
член формулы Тейлора
![]()
 :
:
 при
любом значении х.
Ряд сходится к sin
x
при всех хÎR.
при
любом значении х.
Ряд сходится к sin
x
при всех хÎR.
sin
x
= х
–
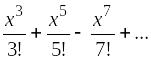
На рисунке 3 изображены графики у = sin x и частичных сумм ряда Маклорена

Рис. 3
Ряды Маклорена основных функций
 ,
область сходимости (–¥;
¥);
,
область сходимости (–¥;
¥);
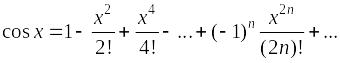 ,
область сходимости (–¥;
¥);
,
область сходимости (–¥;
¥);
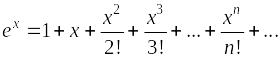 ,
область сходимости (–¥;
¥);
,
область сходимости (–¥;
¥);
 ,
биномиальный ряд с областью сходимости
(–1; 1);
,
биномиальный ряд с областью сходимости
(–1; 1);
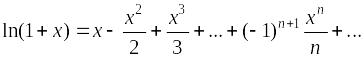 ,
область сходимости (–1;
1];
,
область сходимости (–1;
1];
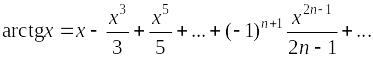 ,
область сходимости [–1;
1].
,
область сходимости [–1;
1].
Пример.
Доказать, что
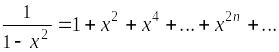 .
.
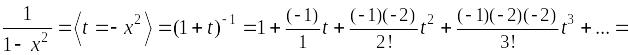
![]()
Область сходимости (–1; 1).
Пример.
Доказать, что arctgх = 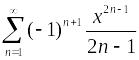 .
.
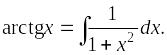

Интегрирование равномерно сходящегося ряда:

 .
.
Область сходимости хÎ[–1; 1].
Пример.
Разложить в ряд Тейлора по степеням
(x – 2)
функцию
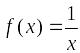 .
.
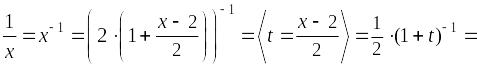
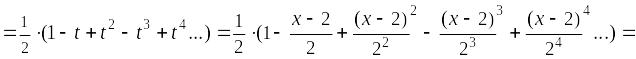
 Область
сходимости хÎ(0;
4).
Область
сходимости хÎ(0;
4).
Применение степенных рядов в приближенных вычислениях
Приближенные вычисления с помощью степенных рядов осуществляются представлением функций их разложениями в сходящиеся степенные ряды, заменой сумм S(x) рядов их частичными суммами Sп(x) и оценкой погрешности получаемых приближенных равенств.
Пример. Вычислить sin1 с точностью до 0,001.
Ряд Маклорена: .
Ряд
Маклорена при х
= 1:
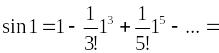
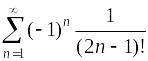 .
.
Знакочередующийся ряд сходится по признаку Лейбница.
Погрешность
вычисления
![]() :
:
 .
.
Сумма
ряда:
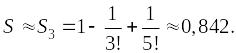
Пример. Вычислить число е с точностью до 0,001.
Ряд
Маклорена:

Ряд
Маклорена при х
=1:
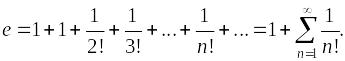
Положительный
ряд
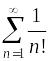 сходится по признаку Даламбера.
сходится по признаку Даламбера.
Остаточный член формулы Тейлора:
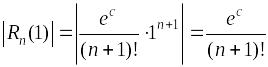 ,
где сÎ(0;
1).
,
где сÎ(0;
1).
Погрешность
вычисления:
 ,
,
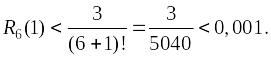
Сумма
ряда:
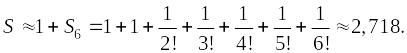
Пример.
Вычислить предел
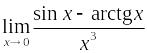 .
.
Ряд
Маклорена:

Ряд
Маклорена:
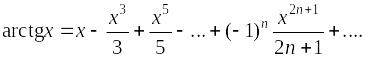
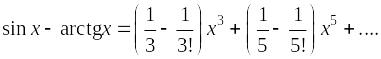
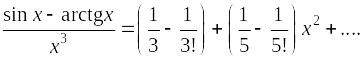

Пример.
Вычислить интеграл
 с точностью до 0,001.
с точностью до 0,001.
Ряд
Маклорена:

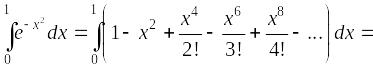


Тема 16 Тригонометрические ряды Фурье
Условия Дирихле: функция f(x) периода Т = 2l непрерывна (либо имеет конечное число разрывов первого рода) и монотонна (либо имеет конечное число экстремумов) на периоде.
Тригонометрический ряд
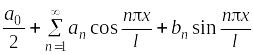 ,
,
где
числовые коэффициенты
![]() и
и
![]() вычисляются по формулам:
вычисляются по формулам:
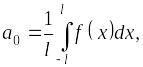
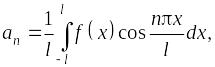
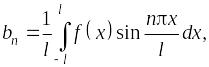
называется рядом Фурье функции f(x).
Теорема.
Если функция f(х)
удовлетворяет условиям Дирихле, то
сумма ряда Фурье S(x)
равна f(x)
в точках
непрерывности и среднему арифметическому
односторонних пределов
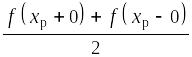 в точках разрыва xр.
в точках разрыва xр.


Рис. 4
Cумма
![]() может быть представлена в виде гармоники
Аnsin(wnx + jn),
т. е. синусоидального колебания с
амплитудой
может быть представлена в виде гармоники
Аnsin(wnx + jn),
т. е. синусоидального колебания с
амплитудой
![]() ,
фазой
,
фазой
 ,
частотой
,
частотой
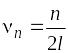 ,
круговой (угловой) частотой
,
круговой (угловой) частотой
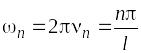 ,
периодом
,
периодом
 (рис. 4).
(рис. 4).
Для четных функций: коэффициенты bn ряда Фурье равны нулю и разложение f(х) содержит только косинусы (разложение по косинусам):
f(х) =  ,
,

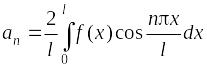 .
.
Для нечетных функций: коэффициенты аn ряда Фурье равны нулю и разложение содержит только синусы (разложение по синусам):
f(х)
=
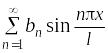 ,
,
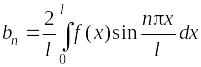 .
.
Рис. 5 |
Рис. 6 |
Если
функция f(х)
задана на отрезке [0; l],
то дополняя ее на отрезке [–l; 0]
четным (рис. 5) или нечетным образом (рис.
6), возможно представление функции f(х)
рядом Фурье, содержащим только косинусы
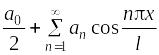 или только синусы
или только синусы
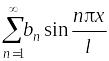 .
Суммы этих рядов есть периодические
функции, определенные на всей числовой
оси и совпадающие на (0; l)
с функцией
f(х)
в точках непрерывности.
.
Суммы этих рядов есть периодические
функции, определенные на всей числовой
оси и совпадающие на (0; l)
с функцией
f(х)
в точках непрерывности.
Пример. Записать разложение в ряд Фурье чётной функции f(х), заданной на отрезке [–2; 2].
Ряд
Фурье для чётной функции:
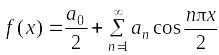 ,
,
где
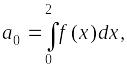
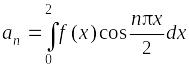 .
.
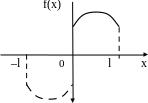
Пример. Функцию
 (рис. 7) периода
(рис. 7) периода
![]() разложить
в ряд Фурье.
разложить
в ряд Фурье.

Рис. 7
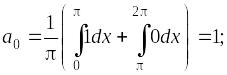
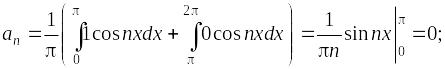

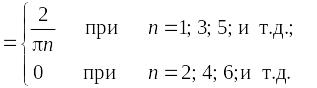
Ряд Фурье:
 .
.
Функция f(x) периодична, постоянна, и имеет разрывы только первого рода. Сумма ряда Фурье в точках разрыва функции f(x) равна 0,5, а в точках непрерывности S(x) = f(x).
Пример. Записать ряд Фурье для периодической функции, график которой представлен на рисунке 8.
Функция f(х): чётная, l = p, f(х) = p – х на отрезке [0; π].
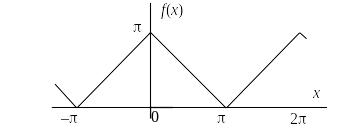
Рис. 8
а0
=
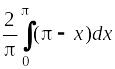 =
=
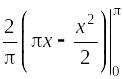 =
=
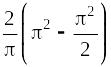 =
p.
=
p.
аn
=
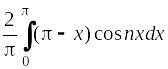 =
=
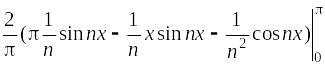 =
=