Тема 13

Знакопеременные ряды

Если положительный ряд (ряд с положительными членами |u_n|) сходится, то сходится и знакопеременный ряд . В этом случае ряд называется абсолютно сходящимся. Ряд сходится условно, если он cходится, а положительный ряд , составленный из модулей u_n, расходится. С абсолютно сходящимися рядами можно обращаться как с конечными суммами (переставлять местами слагаемые, складывать и т.д.).

Ряд , где все , называется знакочередующимся.

Признак Лейбница: знакочередующийся ряд сходится, если выполняются условия:

1) ;

2)

Остаток знакочередующегося ряда имеет знак своего первого члена и не превышает величины , т. е. погрешность D, возникающая при замене суммы знакочередующегося ряда частичной суммой меньше ,

.

Пример. Доказать сходимость ряда , найти приближенно его сумму с точностью 0,01.

Признак Лейбница: ,

члены ряда монотонно убывают.

Знакочередующийся ряд сходится.

Погрешность вычисления : .

Сумма ряда:

Тема 14 Функциональные ряды. Равномерная сходимость

Ряд , членами которого являются функции, называется функциональным. В каждой точке множества определения функций , , функциональный ряд превращается в числовой ряд, который может либо сходиться (точка сходимости функционального ряда), либо расходиться (точка расходимости ряда). Множество точек сходимости ряда образуют область сходимости функционального ряда. В области сходимости частичная сумма ряда есть функция аргумента х.

Определение. Функциональный ряд называется равномерно сходящимся на отрезке [a; b], если на этом отрезке для любого положительного значения e найдется число k такое, что для всех n больших k и любых хÎ[a; b] выполняется неравенство

.

Теорема (признак Вейерштрасса). Если существует сходящийся положительный числовой ряд такой, что для членов функционального ряда справедливы неравенства для всех n и любых хÎ[a; b], то функциональный ряд сходится равномерно на [a; b].

Сумма S(x) равномерно сходящегося ряда непрерывных функций есть непрерывная функция. Ряд, полученный умножением всех членов равномерно сходящегося ряда на ограниченную непрерывную функцию, есть равномерно сходящийся ряд. Равномерно сходящийся на [a; b] ряд можно почленно интегрировать по любому отрезку [a; b]Ì[a; b]:

,

причем получившийся ряд равномерно сходится на [a; b].

Если члены ряда – дифференцируемые функции и ряд, составленный из производных его членов, равномерно сходится на [a; b], то справедливо равенство .

Степенные ряды

Степенным рядом называется функциональный ряд вида

Областью сходимости степенного ряда является интервал , установить который можно по признаку Даламбера. В области сходимости (рис. 1) степенной ряд сходится абсолютно и равномерно, его можно почленно дифференцировать и интегрировать. На границе сходимости (х = a – R и х = a + R) требуется дополнительное исследование ряда.

Расходится Сходится Расходится

a – R a a + R х

Рис. 1

Величина R ³ 0 называется радиусом сходимости. Степенной ряд может сходиться как в одной точке х = a (R = 0), так и на всей числовой оси (R = ¥).

Пример. Найти область сходимости степенного ряда .

–ряд, составленный из модулей:

; .

Признак Даламбера:

Область сходимости: < 1, отсюда –1 < x < 3.

При : числовой ряд сходится по признаку Лейбница.

При : гармонический ряд расходится.

Область сходимости ряда (рис. 2): [–1; 3).

Расходится Сходится Расходится

–3 –2 –1 0 1 2 3 4 х

Рис. 2

Пример. Найти область сходимости степенного ряда .

– положительный ряд, составленный из модулей:

; .

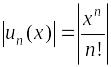Признак Даламбера:

Область сходимости: .