ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА

Федеральное государственное бюджетное образовательное

учреждение высшего образования

“петербургский государственный

университет путей сообщения ИМПЕРАТОРА АЛЕКСАНДРА I”

Кафедра «Высшая математика»

М.А. Шварц

Конспект лекций

по дисциплине

«МАТЕМАТИКА» (Б1.О.7)

для специальности

23.05.05 «Системы обеспечения движения поездов»

по специализациям:

«Автоматика и телемеханика на железнодорожном транспорте»

«Телекоммуникационные системы и сети железнодорожного

транспорта»

«Электроснабжение железных дорог»

Форма обучения – очная, заочная

«Радиотехнические системы на железнодорожном транспорте»

Форма обучения – очная

Раздел 9. Числовые и функциональные ряды. Гармонический анализ

Санкт-Петербург 2020

Тема12

Числовые ряды

Числовым рядом называется выражение 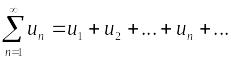, где u_n = f(n) – общий член ряда числа. Конечная сумма n первых членов ряда образуют n-ю частичную сумму ряда. Если существует конечный предел , то ряд сходится, в противном случае ряд расходится. У сходящегося ряда число является суммой ряда. Ряд 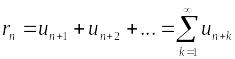называется n-ым остатком ряда. Если ряд сходится, то остаток также сходится (и наоборот). Погрешность вычисления, возникающая при замене суммы сходящегося ряда частичной суммой , равна .

Необходимое условие сходимости ряда. Если ряд сходится, то предел общего члена ряда равен нулю при n®¥ .

Достаточное условие расходимости ряда. Если  ¹ 0, то ряд расходится.

При  = 0 ряд может быть как сходящимся, так и расходящимся.

Пример. Исследовать на сходимость ряд .

.

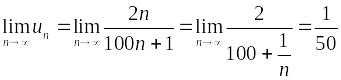Необходимое условие сходимости ряда не выполняется. Ряд расходится.

Пример. Доказать сходимость ряда .

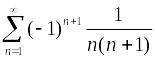Общий член ряда: .

Частичная сумма ряда :

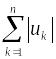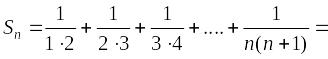
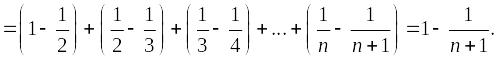
Предел частичной суммы положительного ряда :

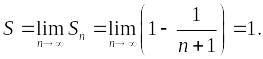
Положительный ряд 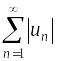сходится.

Знакочередующийся ряд 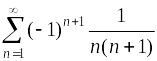сходится абсолютно.

Пример. Доказать необходимый признак сходимости ряда.

Достаточные признаки сходимости положительных рядов

Для положительных рядов , (u_n > 0, v_n > 0 для всех n) справедливы следующие признаки сходимости.

Признак Даламбера: < 1 – ряд сходится;

> 1 – ряд расходится;

При = 1 требуется дополнительное исследование.

Признак Коши: < 1 – ряд сходится;

> 1 – ряд расходится;

При = 1 требуется дополнительное исследование.

Интегральный признак: ряд 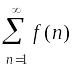и несобственный интеграл одновременно сходятся или расходятся (функция f(x) – непрерывная, положительная, невозрастающая для x ³ a).

Признак сравнения: если члены ряда не превосходят соответствующих членов ряда , т.е. , то из сходимости ряда следует сходимость ряда ; из расходимости ряда следует расходимость ряда .

Предельный признак сравнения: если существует конечный отличный от нуля предел , то ряды и одновременно сходятся или расходятся,.

Пример. Исследовать сходимость ряда .

Признак Даламбера:

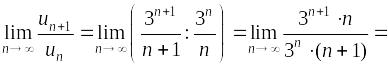
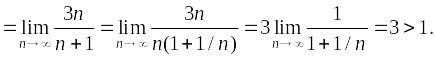
Ряд расходится.

Пример. Исследовать сходимость ряда

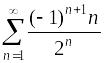
– знакочередующийся ряд:

.

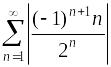– положительный ряд: .

Признак Даламбера:

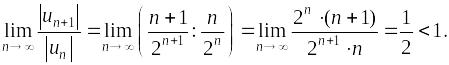
Ряд сходится абсолютно.

Пример. Исследовать сходимость ряда .

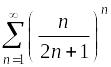– положительный ряд: .

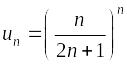Признак Коши:

Ряд сходится.

Пример. Исследовать сходимость гармонического ряда .

– положительный ряд: ,

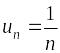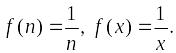
Интегральный признак:

Интеграл расходится, ряд также расходится.

Пример. Исследовать сходимость обобщенного гармонического ряда

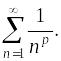
– положительный ряд: , 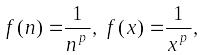р ¹ 1.

Интегральный признак:

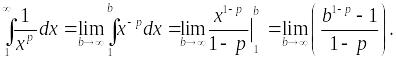
При p < 1 интеграл расходится, ряд 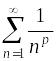также расходится.

При p > 1 интеграл сходится, ряд также сходится.

При р = 1 ряд расходится (см. предыдущий пример).

Пример. Исследовать сходимость ряда .

– положительный ряд; ~ ~

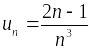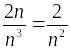Ряд – обощенный гармонический, сходящийся при р > 1.

Предельный признак сравнения:

Ряд сходится.

Пример. Исследовать сходимость ряда .

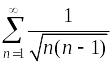– положительный ряд; .

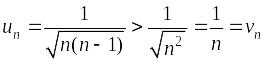Ряд 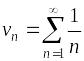– гармонический, расходящийся;

признак сравнения: ;

ряд расходится.