Вариант 29
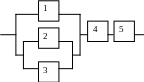
1. На рисунке представлена система из пяти независимо работающих элементов. Обозначим событие, состоящее в том, что элемент « » работает. Используя операции алгебры событий, выразить событие состоящее в том, что система из пяти элементов работает, через события . Найти надежность системы, если надежность каждого элемента равна 0,7.
2. В беспроигрышной лотерее 20 билетов, из них 3 билета в дом отдыха, 10 билетов на турбазу и 7 билетов на стадион. Три друга приобрели по одному билету лотереи. Найти вероятность того, что а) хоть один из них получил билет на стадион; б) все получили билеты на стадион.
3. Электронная база данных содержит 15 вопросов по алгебре, 10 – по геометрии. Абитуриент последовательно выбирает 2 вопроса. Найти вероятность того, что он выберет вопросы по разным разделам при условиях а) выбранный вопрос в электронной базе сохраняется; б) выбранный вопрос из электронной базы удаляется.
4. В водоеме, богатом рыбой, обитают рыбы видов и в соотношении 7: 3. На каждые 100 рыб вида приходится 65 самцов, а на каждые 100 рыб вида приходится 55 самцов. Наудачу отлавливают одну рыбу. Найти вероятность того, что это самец.
5. Магазин получает для продажи однотипную продукцию с двух баз в соотношении 1:2. Вероятность брака продукции первой базы – 0,1, второй – 0,15. Наудачу отобранная продукция оказалась бракованной. С какой базы она вероятнее всего прибыла.
6. Вероятность того, что в течение суток машина потребует ремонта, равна 0,1. Фирма для работы арендовала 10 автомашин. Найти вероятности того, что среди арендованных машин а) только 2 потребуют ремонта; б) не менее 2, но не более 4 потребуют ремонта. Найти наивероятнейшее число автомашин, требующих ремонта.
7. В предыдущей задаче фирма арендовала 150 автомашин. Найти вероятности событий: а) потребуют ремонта 18 машин: б) не менее 18, но не более 23 машин потребуют ремонта.
Вариант 30
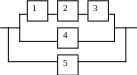
1. На рисунке представлена система из пяти независимо работающих элементов. Обозначим событие, состоящее в том, что элемент « » работает. Используя операции алгебры событий, выразить событие состоящее в том, что система из пяти элементов работает, через события . Найти надежность системы, если надежность каждого элемента равна 0,7.
2. В классе 15 мальчиков и 10 девочек. Наудачу отобраны три ученика. Найти вероятность того, что среди них а) хотя бы один мальчик; б) только один мальчик.
3. На карточках изображены числа от 1 до 10. Наудачу последовательно извлекают 2 карточки. Найти вероятность того, что число на второй карточке больше числа на первой карточке в предположениях а) карточки в массив не возвращаются; б) карточки в массив возвращаются.
4. Известно, что 5% мужчин и 0,25% женщин дальтоники. В компании мужчин в 2 раза больше, чем женщин. Наудачу выбирают одного человека. Найти вероятность того, что он не дальтоник.
5. Работа некоторой системы обеспечивается одним из трех контролирующих устройств, которые автоматически включаются в работу с вероятностями 0,2; 0,3; 0,5 соответственно. Вероятности безотказной работы контролирующих устройств равны соответственно 0,9; 0,8; 0,7. Известно, что система отказала. Найти вероятность того, что включилось первое контролирующее устройство.
6. Вероятность поймать рыбу при одном забрасывании удочки в богатом рыбой водоеме равна 0,1. Удочку забросили 10 раз. Найти вероятности того, что поймано а) только 2 рыбы; б) не менее 2 рыб; в) не менее 3, но не более 5 рыб. Найти наивероятнейшее число рыб, пойманных в водоеме, при десяти набрасываниях удочки.
7. ОТК проверяет 500 изделий на брак. Вероятность того, что изделие бракованное, равна 0,1. Найти вероятности событий: а) бракованных изделий 53; б) бракованных изделий не менее 53, но не более 65.