
- •М.А. Шварц
- •Конспект лекций
- •23.05.05 «Системы обеспечения движения поездов»
- •Раздел 8. Дифференциальные уравнения Санкт-Петербург 2020 Тема 1
- •1. Дифференциальные уравнения первого порядка
- •Метод Эйлера приближенного решения задачи Коши
- •Тема 2 Уравнения с разделяющимися переменными
- •Однородные уравнения
- •Тема 3 Линейные дифференциальные уравнения
- •Уравнение Бернулли
- •Уравнения в полных дифференциалах
- •Тема 4 дифференциальные уравнения высших порядков
- •Понижение порядка уравнения
- •Тема 5 Линейные дифференциальные уравнения высших порядков
- •Тема 6 Линейные однородные уравнения с постоянными коэффициентами
- •Линейные неоднородные уравнения с постоянными коэффициентами. Метод Лагранжа
- •Темы 7,8 Линейные неоднородные уравнения с постоянными коэффициентами. Метод неопределенных коэффициентов
- •Контрольные тесты
- •Тема 9 системы дифференциальных уравнений
- •Системы линейных уравнений с постоянными коэффициентами
- •Решение однородных систем линейных уравнений
- •Контрольные тесты
- •Тема 10 Оригиналы и изображения
- •Теоремы операционного исчисления
- •Изображения основных функций
- •Тема 11 Решение дифференциальных уравнений
- •Решение систем уравнений
- •2 Контрольные тесты
Контрольные тесты
№ |
Задание |
Ответ |
1 |
В
матричной форме записи системы
дифференциальных уравнений
1)
|
|
2 |
Порядок
системы
|
|
3 |
Дифференциальное
уравнение
1)
|
|
4 |
Нормальная
система эквивалентная
1)
|
|
5 |
Нормальная
система эквивалентная
дифференциальному
уравнению
1)
|
|
6 |
Количество
произвольных постоянных в общем
решении системы
дифференциальных уравнений
|
|
7 |
Определитель
Вронского
1) 0 2) 2х2 3) 2х3 4) 2х4 |
|
8 |
Определитель
Вронского
1) 0 2) 2 3) х3 4) х4 |
|
9 |
Определитель Вронского для функций
1)
|
|
10 |
Выберите линейно зависимые векторные функции
1)
|
|
11 |
Для
системы
1)
3)
|
|
12 |
Для
системы
1)
3)
|
|
13 |
Для системы характеристическое уравнение имеет вид
1) 2 – 2 + 1 = 0 2) 2 + 1 = 0 3) 2 – 1 = 0 4) 2 – 2 = 0 |
|
14 |
Общее решение системы имеет вид
1)
3)
|
|
15 |
Собственные векторы матрицы А системы равны
1)
|
|
16 |
Частное
решение системы д.у.
1)
3)
|
|

 матрица системы имеет вид
матрица системы имеет вид
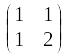 2)
2)
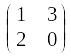 3)
3)
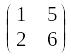 4)
4)
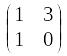
 равен
равен эквивалентное
нормальной
системе имеет вид
эквивалентное
нормальной
системе имеет вид
 имеет вид
имеет вид
 2)
2)
 3)
3)
 4)
4)

 имеет вид
имеет вид
 2)
2)
 3)
3)
 4)
4)

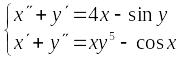 равно
равно
 равен
равен равен
равен ,
,
 имеет вид
имеет вид 2)
2)
 3)
3)
 4)
4)

 2)
3)
2)
3)
 4)
4)

 характеристическое уравнение имеет
вид
характеристическое уравнение имеет
вид 2)
2)

 4)
4)

 характеристическое уравнение имеет
вид
характеристическое уравнение имеет
вид 2)
2)

 4)
4)

 2)
2)

 4)
4)

 2)
2)
 3)
3)
 4)
4)

 удовлетворяющее начальным условиям
удовлетворяющее начальным условиям
 имеет вид
имеет вид
 2)
2)

 4)
4)
