Линейные неоднородные уравнения с постоянными коэффициентами. Метод Лагранжа

Теорема. Общее решение неоднородного уравнения у_о.н. есть сумма любого частного решения этого уравнения у_ч.н. и общего решения соответствующего однородного уравнения у_о.н. = у_о.о. + у_ч.н..

В соответствии с теоремой задача нахождения общего решения линейного неоднородного д.у. сводится к нахождению какого-либо его частного решения у_ч.н. (при известном у_о.о.). Если правая часть уравнения , то частное решение ищется в виде суммы частных решений у_ч.н., отвечающих каждому из слагаемых : .

Пусть . Соответствующее однородное уравнение имеет фундаментальную систему решений и общее решение . Рассмотрим два метода нахождения частного решения у_ч.н..

Метод вариации произвольных постоянных состоит в нахождении частного решения в виде , где функции являются решением системы уравнений Определитель системы есть определитель Вронского , который для функций не обращается в ноль. Система совместна и определена (имеет единственное решение).

Для уравнения п-го порядка

,

частное решение ищется в виде у_ч.н. при общем решении соответствующего однородного уравнения . Система уравнений для нахождения функций имеет вид

Темы 7,8 Линейные неоднородные уравнения с постоянными коэффициентами. Метод неопределенных коэффициентов

Метод неопределённых коэффициентов применяется для нахождения частного решения линейного неоднородного д.у., если правая часть уравнения имеет вид где , – многочлены степени п и т соответственно. Частное решение ищется в виде

,

где ,

r – количество совпадений числа с корнями характеристического уравнения,

, – полные многочлены степени k с неопределёнными (буквенными) коэффициентами.

Подстановка у_ч.н., у_ч.н.,…, у⁽ⁿ⁾_ч.н. в исходное уравнение превращает его в тождество и позволяет получить совместную определённую систему линейных уравнений относительно искомых коэффициентов многочленов , .

Частные случаи соответствия правой части д.у., числа  и вида частного решения представлены в таблице 3.

Таблица 3

Правая часть уравнения f(х)		Вид частного решения уч.н.
Аеах	а	xrMeax
(Ах + В)еах	а	xr (Mх + N) eax
(Ах2 + Вх + С)еах	а	xr (Mх2 + Nх + K) eax
А	0	xrM
Ах + В	0	xr (Mх + N)
Ах2 + Вх + С	0	xr (Mх2 + Nх + K)
Acosbх, Вsinbх, Acosbx + Bsinbx	bi	xr(Мcosbх + Nsinbх)
eaxАcosbх, eaxВsinbх, eax (Acosbx + Bsinbx)	a+bi	xreax(Мcosbх + Nsinbх)

Пример. Методом вариации произвольных постоянных найти общее решение уравнения .

Соответствующее однородное уравнение: .

Характеристическое уравнение: .

Корни характеристического уравнения: , .;

Фундаментальная система решений: , .

Общее решение однородного д.у.: .

Частное решение неоднородного д.у.: у_ч.н. .

Система уравнений для нахождения функций :

Решения системы: , .

Искомые функции: ,

.

Частное решение при :

.

Общее решение неоднородного д.у.:

.

Пример. Записать вид частного решения неоднородного д.у., если правая часть этого уравнения и среди корней характеристического уравнения нет нулевого корня.

Число  = 0 не совпадает с корнями характеристического уравнения: r = 0.

Вид частного решения: y_ч.н. = Mх² + Nх + K (строка 6 таблицы 3).

Пример. Установить вид частного решения уравнения у² – 5у¢ = 7х + 8.

Соответствующее однородное уравнение: у² – 5у¢ = 0.

Характеристическое уравнение: ² – 5 = 0.

Корни характеристического уравнения ₁ = 5, ₂ = 0;

Одно совпадение числа  = 0 с корнем характеристического уравнения: r = 1.

Правая часть дифференциального уравнения: f(x) = 7x +8.

Вид частного решения:

y_ч.н. = х(Mx + N) = Mx² + Nх (строка 5 таблицы 3).

Пример. Записать вид частного решения неоднородного д.у., если и среди корней характеристического уравнения есть пара комплексных сопряжённых корней

Число повторений r числа среди корней характеристического уравнения: 1.

Вид частного решения: .

Пример. Найти общее решение дифференциального уравнения

Однородное уравнение:

Характеристическое уравнение: ² + 1 = 0.

Корни характеристического уравнения: , .

Фундаментальная система решений: , .

Общее решение однородного уравнения:

Правая часть дифференциального уравнения: .

Число не совпадает с корнями характеристического уравнения: r = 0.

Вид частного решения:

(строка 7 таблицы 4.3).

Производные частного решения: , .

После подстановки , в уравнение :

M = 0, N = –1.

Частное решение д.у.:

Общее решение д.у.:

Пример. Найти общее решение уравнения .

Однородное уравнение: .

Характеристическое уравнение: ² – 2 + 1 = 0.

Корни характеристического уравнения: , .;

Фундаментальная система решений: .

Общее решение однородного уравнения: .

Правая часть дифференциального уравнения: .

Два совпадения числа с корнями характеристического уравнения: r = 2.

Вид частного решения:

(строка 3 таблицы 3).

Подстановка , в уравнение приводит к равенству , откуда , .

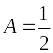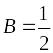Частное решение: .

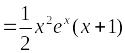Общее решение: .

Пример. Найти решение уравнения ,

удовлетворяющее начальным условиям , .

Однородное уравнение: .

Характеристическое уравнение: ² – 1 = 0.

Корни характеристического уравнения: , .

Фундаментальная система решений: .

Общее решение однородного уравнения: .

Правая часть дифференциального уравнения: .

Число  = 0 не совпадает с корнями характеристического уравнения: r = 0.

Вид частного решения: (строка 6 таблицы 3).

Подстановка , , в уравнение .

Приравнивание коэффициентов при одинаковых степенях х в левой и правой частях равенства приводит к системе

Неопределенные коэффициенты: M = –1, N = –2, K = –1.

Частное решение: .

Общее решение: .

Производная общего решения: .

При , :

Значения произвольных постоянных: С₁ = 3, С₂ = –1.

Решения задачи Коши: .

Пример. Найти частное решение уравнения .

, .

Частное решение для f₁(x): .

Частное решение для f₂(x): .

Частное решение для f(x): .

Пример. Найти частное решение уравнения .

Однородное уравнение: .

Характеристическое уравнение: ² + ² = 0.

Корни характеристического уравнения: , .

Правая часть дифференциального уравнения: .

Число  = i совпадает с корнем характеристического уравнения.

Вид частного решения (строка 7 табл. 3):

Производные частного решения:

. Подстановка в уравнение :

.

Значения неопределенных коэффициентов:

Частное решение: .

Пример. Доказать, что если – фундаментальная система решений однородного д.у. , то для неоднородного д.у. решение системы задает частное решение .

Производная :

.

Пусть функции , таковы, что .

Тогда .

Подстановка , в уравнение приводит к равенству

или

Выражения в скобках левой части равенства обращаются в ноль и уравнение принимает вид .