Тема 10 Оригиналы и изображения

Определение. Функция , определенная на интервале (–; ), называется оригиналом, если

1) f(t)  0 при ;

2) f(t) – непрерывна (либо имеет конечное число разрывов первого рода на любом конечном отрезке);

3) существуют такие вещественные числа М > 0 и s₀  0, что 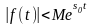для всех положительных значений t.

Для всякого оригинала f(t) существует единственная функция 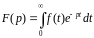комплексной переменной p = s + i, определенная в комплексной полуплоскости Rep = s >  (рис. 1). Функция называется изображением оригинала f(t). Правая часть равенства называется интегралом Лапласа, а переход от оригинала f(x) к изображению F(p) – преобразованием Лапласа. Запись f(t)  F(p) означает, что оригиналу f(t) соответствует изображение F(p) (и наоборот).

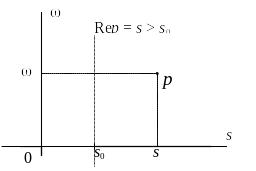
Рис. 1

Простейшим оригиналом является функция Хэвисайда – единичная ступенчатая функция (рис. 2):

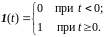
Изображение функции Хэвисайда:

.

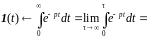
Рис. 2

Функция Хэвисайда используется для представления сигналов, включающихся в определённый момент времени. Если (t) удовлетворяет условиям 2 и 3, то функция f(t) = (t)1(t) является оригиналом. Далее вместо произведения (t)1(t) используется запись f(t), где f(t)  0 при t < 0.

Пример. Найти изображение функции ƒ(t) = е^аt, аR.

F(p) =

Пример. Найти изображение функции ƒ(t) = sh(ωt) = , R.

Пример. Найти изображение функции ƒ(t) = sin(ωt), R.

Формула Эйлера: е^i = cos + isin, е^–i = cos – isin.

Комплексное представление функции sin(ωt): .

.

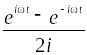Пример. Найти изображение функции ƒ(t) = t.

формула интегрирования по частям

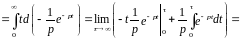
Теоремы операционного исчисления

Теорема линейности. с₁f₁(t) + с₂f₂(t)  с₁F₁(p) + с₂F₂(p),

если f₁(t)  F₁(p), f₂(t)  F₂(p), с₁, с₂ – постоянные.

Теорема запаздывания. f(t – )  e^–pF(p),

если  > 0, f(t)  F(p) (рис. 3, 4).

Рис. 3

Рис. 4

Теорема подобия. f(t)   , если  > 0, f(t)  F(p).

Теорема смещения. е^–tf(t)  F(p + ), если f(t)  F(p).

Теорема дифференцирования оригиналов.   рF(p) – f(0), если f(t)  F(p).

Следствие. Если ƒ(t) – п-раз дифференцируемая функция, все производные которой являются оригиналами, то для производной k-го порядка ( ), справедлива формула:

.

При нулевых начальных условиях последняя формула принимает вид   .

Пример. Найти изображение функции

f(t) – единичный импульс (рис. 5).

Представление единичного импульса в виде разности двух функций (рис. 2, 6): f(t) = 1(t) – 1(t – 1).

Рис. 5

1(t – 1) Рис. 6

Изображение функции Хэвисайда: 1(t)   .

Теорема запаздывания для функции Хэвисайда: 1(t – 1)   ;

.

Пример. Доказать теорему дифференцирования оригиналов:

   , если f(t)  F(p).

   формула интегрирования по частям

Изображения основных функций

В таблице 1 приведены изображения часто встречающихся на практике функций.

Таблица 1

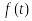
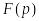
№	Оригинал	Изображение	№	Оригинал	Изображение
1	1(t)		8
2			9
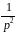
3			10
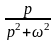
4			11
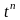
5			12
6			13
7			14

Нахождение оригинала осуществляется представлением изображения суммой табличных изображений и применением теоремы линейности преобразования Лапласа. Имеют место две теоремы разложения, позволяющие находить оригиналы весьма широкого класса функций.

Теорема. Если изображение представляет собой правильную рациональную дробь, , где – многочлены степени m и n соответственно (m < n), то оригинал ƒ(t) есть сумма оригиналов элементарных рациональных дробей:

1) ;

2) ;

3) ,

 = –b/2, ² = c – b²/4, b² – 4c < 0.

Замечание. Нахождение оригинала элементарной дроби четвертого типа при k  2 предлагается изучить самостоятельно.

Теорема. Если изображение функции может быть представлено функциональным рядом по степеням ,

,

сходящимся к F(p), то оригинал f(t) представляется в виде степенного ряда

,

сходящегося при всех t.

Пример. Найти оригинал функции F(p) = .

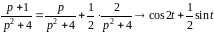– пункты 3, 4 таблицы 1.

Пример. Найти оригинал изображения .

Числители дробей одинаковы: .

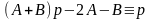Система для нахождения значений неопределенных коэффициентов А, В:

Решение системы: , .

Разложение F(p) на элементарные дроби: .

Искомый оригинал (табл. 1):

Пример. Найти изображение ступенчатой функции, заданной на промежутке [0; +), четыре ступени которой представлены на рисунке 7.

Рис. 7

Аналитическое выражение функции f(t):

Изображение для f (t):

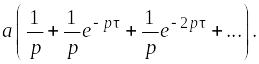
Слагаемые в скобках образуют убывающую бесконечную геометрическую прогрессию с знаменателем .

Сумма прогрессии:

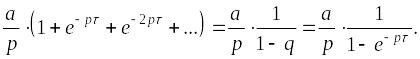
Пример. Найти изображение импульсной дельта-функции Дирака если .

Рассмотрим прямоугольный импульс

при любом значении h.

Представление функции в виде разности двух функций Хэвисайда:  =  .

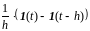Изображение прямоугольного импульса: .

Изображение равно пределу при h  0 изображения :