Тема 4 Надежность систем

Надежностью системы называется вероятность ее безотказной работы в течение заданного промежутка времени [0; Т]. Пусть A_i – событие, состоящее в том, что i – ый элемент системы отработал без отказа до момента T, – отказ i – ого элемента, . Работоспособность системы в целом зависит как от надежности ее элементов, так и от структуры системы. Пусть система состоит из двух элементов, отказы которых происходят независимо друг от друга. Возможны два варианта.

1) Отказ системы происходит при отказе хотя бы одного элемента системы. Надежность системы определяется по формуле умножения вероятностей . Схема надежности в этом случае обозначается последовательным соединением элементов (рис. 9).

Рис. 9

2) Работу системы обеспечивает хотя бы один работающий элемент.

Надежность системы определяется по формуле сложения вероятностей P(А) = P(А₁) + P(А₂) – P(А₁)  P(А₂). Схема надежности в этом случае обозначается параллельным соединением элементов (рис. 10).

Рис. 10

Пример. Определить надежность системы из шести независимо работающих элементов (рис. 11). Надежности элементов:

Рис. 11 Рис. 12 Рис. 13

Надежность элементов «2» и «3»: р_2,3 = р₂  р₃.

Надежность элементов «4» и «5»: р_4,5 = р₄ + р₅ – р₄  р₅.

Рис. 12 – эквивалентная схема надежности «1», «2, 3», «4, 5», «6».

Надежность элементов «1» и «2, 3»: р_1,2,3 = р₁ + р_2,3 – р₁  р_2,3.

Надежность элементов «6» и «4, 5»: р_4,5,6 = р₆ + р_4,5 – р₆  р_4,5.

Рис. 13 – эквивалентная схема надежности «1, 2, 3», «4, 5, 6».

Надежность элементов «1, 2, 3» и «4, 5, 6»:

р_1,2,3  р_4,5,6 =  0,864.

Тема 5 Формула полной вероятности. Формула Байеса

Вероятность события А (доопытная, априорная) находится по формуле полной вероятности:

Р(А) = ,

если событие А может произойти только вместе с одним из n событий Н_i (гипотез), единственно возможных , попарно несовместных (Н_i  Н_j = ; ).

Если событие А произошло, то послеопытная (апостериорная) вероятность гипотезы Н_i определяется по формуле Байеса:

Р(Н_i/А) = = .

Пример. В четырех урнах содержится по 3 белых и 7 чёрных шаров. Во остальных шести урнах – по 5 белых и 15 чёрных шаров. Найти вероятность того, что

1) шар, извлечённый из наудачу выбранной урны, будет белый;

2) извлечённый белый шар находился во второй группе урн.

Обозначим А = {извлечён белый шар}, Н₁ = {выбрана 1-я группа урн}, Н₂ = {выбрана 2-я группа урн}.

Р(Н₁) = , Р(Н₂) = .

1) Р(А/Н₁) = , Р(А/Н₂) = .

Р(А) = Р(Н₁)Р(А/Н₁) + Р(Н₂)Р(А/Н₂) =

2) Р(Н₂/А) = .

Пример. Доказать формулу полной вероятности.

Пример. Доказать формулу Байеса.

Р(Н_i/А) = = .

Тема 6

Схема Бернулли

Испытания называются независимыми, если вероятность события А в каждом испытании не зависит от исходов других испытаний. Схема Бернулли – последовательность n независимых испытаний, в каждом из которых событие А может либо произойти («успех»), либо не произойти («неудача»). Вероятность «успехов» и «неудач» в испытаниях не меняется: Р(А) = р, . Вероятность того, что в n испытаниях число _n «успехов» равно m (0  m  n), вычисляется по формуле Бернулли:

Р(_n = m) = ,

где − число сочетаний из n по m элементов.

Вероятность того, что в n испытаниях произойдет от m₁ до m₂ «успехов» (0  m₁  m₂  n):

.

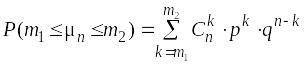Наивероятнейшее число «успехов» в испытаниях определяется двойным неравенством .

Пример. В мишень стреляют четыре раза. Вероятность поражения при одном выстреле 0,8. Определить вероятность того, что мишень будет поражена ровно два раза.

Параметры схемы Бернулли: р = 0,8; q = 0,2; n = 4; m = 2.

.

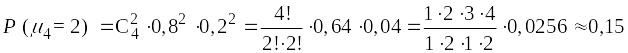Пример. В мишень стреляют четыре раза. Вероятность поражения при одном выстреле 0,8. Определить вероятность того, что мишень будет поражена хотя бы один раз.

Параметры схемы Бернулли: р = 0,8; q = 0,2; n = 4.

= 1−P( = 0) = 1 – 0,2⁴ = 0,9984.

Пример. Трасса, по которой следует автомобиль, имеет 5 перекрестков. Вероятность того, что при подъезде к перекрестку горит зеленый свет (путь автомобилю открыт) равна 0,6. Найти наивероятнейшее число m₀ остановок автомобиля на трассе и вероятность этого события.

Событие – автомобиль перекресток проехал с остановкой.

Параметры схемы Бернулли: р = 0,4; q = 0,6; n = 5.

Наивероятнейшее число остановок автомобиля : для целых значений m₀ = 2.