Тема 1 Испытания и события

Испытание – осуществление определенных действий в условиях, которые можно повторить. Событие – результат испытания.

Событие , которое не может произойти в конкретном испытании, называется невозможном, событие , которое всегда происходит, – достоверным. Случайным считается событие А, которое может в испытании как произойти, так и не произойти. События, которые вместе в одном опыте осуществиться не могут, являются несовместными. Событие , состоящее в том, что А не произошло, называется противоположным событию А.

События и действия над ними могут быть проиллюстрированы диаграммами Венна. Испытание моделируется случайным выбором точки в области , а принадлежность этой точки закрашенной фигуре является некоторым событием. На рисунке 1 область  изображена в виде прямоугольника, событие А – выбор точки внутри треугольника, событие – выбор точки вне треугольника (рис. 2).

Рис. 1 Рис. 2

А  В – событие А включено в событие В (выбор точки внутри квадрата), если событие В всегда происходит, когда происходит А (рис. 3).

Рис. 3

События А и В эквивалентны (А = В), если А  В и В  А.

Сумма событий А + В (объединение А  В) – происходит хотя бы одно из этих событий (или А или В или А и В вместе). На рисунке 4 тонировано событие А + В.

Рис. 4

Произведение событий АВ (пересечение А  В) – происходят оба события (и А и В).

Рис. 5

Разность событий А\В – происходит А и не происходит В.

Рис. 6

Справедливы следующие соотношения:

1. ;

2. ;

3. 

4. ;

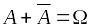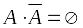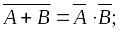
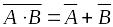5. , если события А и В несовместны, и наоборот.

События А₁, А₂,…, А_n называются единственно возможными, если хотя бы одно из них всегда происходит в результате испытания, т.е. их сумма (объединение) является достоверным событием: А₁ + А₂ +…+ А_n = . События А₁, А₂,…, А_n называются попарно несовместными, если произведения (пересечения) различных пар событий являются невозможным событием: А_i  А_j = ; События А₁, А₂,…, А_n образуют полную группу событий, если они единственно возможны и попарно несовместны. Например, события А и образуют полную группу, т.к. они вместе они осуществится не могут, но одно из них обязательно произойдет.

Относительная частота событий

Относительной частотой (или кратко «частотой») w_n события А в серии испытаний называется отношение

,

где n_А – число испытаний, в которых зафиксировано событие А;

n – общее число испытаний.

Свойства частоты:

1) w_n() = 1;

2) w_n() = 0;

3) ;

4) w_n(АВ) = , если события А и В несовместны;

5) , если события А и В несовместны;

6) ;

7) , если А  В.

В теории вероятностей изучаются случайные явления, в которых частота события обладает свойством статистической устойчивости: при увеличении числа испытаний n частота стабилизируется и приближается к определенному числу.

Пример. Студент присутствовал на восьми семинарах из десяти. Какова относительная частота пропуска студентом семинаров?

Пример. Доказать, что , если события А и В несовместны.

Пусть в результате n опытов событие А произошло n_А раз, а событие В – n_В раз. События А и В несовместны, поэтому число опытов, в которых произошло А или В, равно n_А + n_В.